概率分布的实函数实现问题
2011-11-22易利亚
易利亚
(贵州大学人民武装学院,贵阳 550025)
概率分布的实函数实现问题
易利亚
(贵州大学人民武装学院,贵阳 550025)
基于一维随机变量,通过阐释概率分布实函数实现的内在本质,给出了概率分布实函数实现的一个充分必要条件,得到分布函数族及其连续性特征,揭示出概率论中分布函数定义所蕴含的合理性和深刻性.
概率论;概率分布的实函数实现;分布函数族;连续性
1 引 言
在柯尔莫哥洛夫将概率概括为“非负的、规范的、可列可加的集函数”后,概率便在测度论中获得了最深刻的数学本质[1],这使得在一般意义下通过研究概率分布来达到对随机现象统计规律性的揭示有了理论支撑.这就是分布函数问题.
分布函数问题更一般的提法是:概率分布的实函数实现问题.根据实分析理论,一定条件下几乎处处相等的实函数都可作为给定随机变量的概率分布函数,表明能实现概率分布的实函数具有特定的结构,它们有着区别于其它实函数的共同本质.然而概率论所定义的两型分布函数F1(x)=P{ξ∈(-∞,x]}与F2(x)=P{ξ∈(-∞,x)}在连续性质上所表现出来的不一致,常使学习者对这种共同本质“莫衷一是”,这在一定意义上影响了分布函数概念认知的完备性.
基于此,笔者对概率分布的可实函数实现性、概率分布函数区别于其它实函数的本质特征、概率分布函数的内在结构三个方面进行了讨论,给出了概率分布实函数实现的一个充分必要条件,揭示了分布函数的族结构及其连续性特征,以此来阐释概率论所给定义的合理性和深刻意涵,旨在深化对分布函数概念的认识.
2 概率分布实函数实现的本质
2.1 概率分布实函数实现的概念.
概率论在把随机现象转变成数学问题的过程中,经历了两次抽象.第一次抽象是通过引入随机事件概念,建立起基于σ-代数的概率空间(Ω,F,P).第二次抽象是在(Ω,F,P)的基础上,通过引入随机变量概念,建立起从样本空间Ω到实数集R上的映射关系,从而随机现象的问题就可以借助Borelσ-代数,用实分析的思想和方法来加以讨论.
如果说第一次抽象奠定了公理化概率论的基础,那么第二次抽象的理论价值在于,它提示了随机变量作为(基本)随机事件的映射虽然是随机而变的,它的值不能事先确定,但对于给定的x,事件{ξ∈(-∞,x]}(定义为{ω∈Ωξ(ω)∈(-∞,x]}∈F )或{ξ∈(-∞,x)}(定义为{ω∈Ω(ω)∈(-∞,x)}∈F )的概率遵循着某种“规则性”:两型集{ξ∈(-∞,x]},{ξ∈(-∞,x)}的概率可由x按某种法则唯一地确定.这表明,概率分布总是可以实函数实现的.
但是,现有分布理论把这种可实函数实现性认知为随机变量ξ取(-∞,x]型集或(-∞,x)型集时,其概率P(·)可用x的函数来“表示”,而当出现截然不同的连续性时,却没有对这种对立给出相应的阐释.这不能不说是一个欠缺.
事实上,概率的测度本质决定了概率分布在一般意义下是不可能用实函数来“表示”的,因为倘若如此,概率就无需再言什么测度本质了.所给两型定义实际上也并没有完全实现用实函数来“表示”集函数,这从它们对概率分布的描述时不得不借助实函数的单侧极限手段就可见出.
其实正是这种借助,刚好提示了概率分布实函数实现的内在规定性:随机变量的概率分布只能是用实函数来“描述”的.两型分布函数也仅是表明,第一型当点集取(-∞,x]型集时,概率P(·)的分布可用x的函数F1(x)来表示,而当点集取(-∞,x)时,就只能用F1(x-0)来表示了;同样,第二型在点集取(-∞,x)时,概率P(·)的分布可用x的函数F2(x)来表示,而当点集取(-∞,x]时,就只能用F1(x+0)来表示.
因而从根本上讲,概率分布所遵循的“规则性”决定了其实函数实现的单侧极限表示性,这就是概率分布实函数实现的本质.换句话说,概率分布的实函数实现是通过实函数的单侧极限表示来实现的.这种认识的合理性不仅可在F1(x),F2(x)描述同一随机变量概率分布时所表现出来的差异中得到传达,而且在L-S测度论中可以严格证明.
基于上面的认识,在概率空间(Ω,F,P)中,(-∞,x]或(-∞,x)型集的概率总可以用一个实函数的单侧极限来表示,其一般形式为:

为此,可给出概率分布实函数实现的如下定义.
定义1 设ξ是(Ω,F,P)上的随机变量,F(x)是定义在R上的函数.若
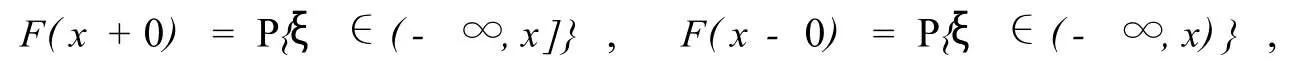
则称P(·)的分布在R上是可实函数实现的,F(x)叫随机变量ξ的概率分布函数,简称为分布函数.
此定义下的F(x)有着如下基本性质.
定理1 设F(x)是随机变量ξ的分布函数,则
(i)F(x)单调不减;
(ii)F(-∞)=0,F(+∞)=1.
证(i)用反证法.假设F(x)非单调不减,则至少存在一点x0∈R,有
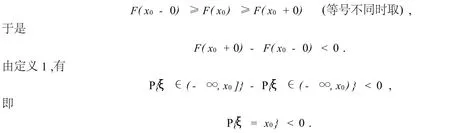
这与概率的非负性矛盾,所以原结论成立.


(ii)由结论(i),任给t>0,有定理1的重要意义在于,它揭示了概率分布函数区别于其它实函数的重要特征:它是定义在R上的非负、规范、单调不减函数.
应用L-S测度理论可以证明,定义在R上的非负、规范、单调不减函数F(x)所确定的L-S测度必是概率测度,因而F(x)必是该概率空间某一随机变量的分布函数.读者可参见文献[2]自己给出证明.
2.2 概率分布实函数实现定理.
文献[3]曾对引言中的两型分布函数的异同作过具体比较.遗憾的是,该文作者未能进一步揭示出两定义蕴涵着的统一本质.这就是下面的定理.
定理2(概率分布的实函数实现定理) 定义在R上的函数F(x)是给定随机变量ξ的分布函数的充分必要条件是,F(x)可表示成如下形式:
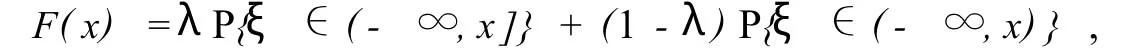
这里,当在F(x)的连续点时,λ∈R;当在F(x)的间断点时,λ∈[0,1].
证先证必要性.设F(x)是给定随机变量ξ的分布函数,因为单调不减,故∀x∈R,

则m,n均为非负数.当m,n不同时为0时,F(x)在x点非连续.不妨设n≠0,有

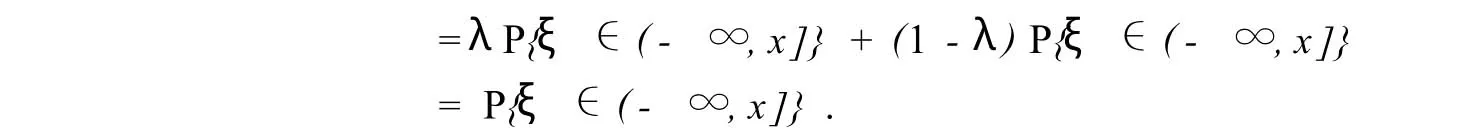
同理可证,F(x-0)=P{ξ∈(-∞,x)}.所以由定义1知,F(x)是给定随机变量ξ的分布函数.
定理2表明,概率分布函数值由(-∞,x]型集、(-∞,x)型集的概率值及参数λ完全确定,因而它深刻地反映了概率分布实函数实现的全部本质.
特别地,在定理2中,当λ=1时,F(x)=P{ξ∈(-∞,x]}=F1(x);当λ=0时,F(x) =P{ξ∈(-∞,x)}=F2(x).可见F1(x),F2(x)都是概率分布函数的特殊情形.
3 分布函数的连续性与结构
3.1关于连续性的若干结论.
下面是定理2的三个推论,它们较好地揭示了分布函数的连续性本质.
推论1 设F(x)是随机变量ξ的分布函数,则F(x)在x0点连续的充分必要条件是

证由定理2知显然成立.
称概率值P{ξ=x0}为分布函数F(x)在x0点的跃度,它的一般形式为
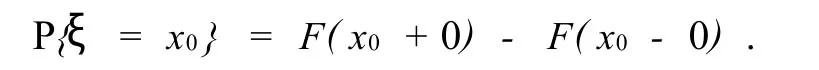
推论2 设F(x)是随机变量ξ的分布函数,x0是其间断点,则当λ=1时,F(x)在x0点是右连续的;当λ=0时,F(x)在x0点是左连续的;当0<λ<1时,F(x)在x0点是无单侧连续的.
证只证最后一个结论,用反证法.不妨设F(x)在x0点左连续,则F(x0-0)=F(x0),有

得λP{ξ=x0}=0.而x0是间断点,根据推论1,P{ξ=x0}≠0,故λ=0,与0<λ<1矛盾.
推论2表明,单侧连续并非分布函数的本质属性,两型定义在连续性上的对立,实在是“黑马”与“白马”的对立,而在此推论下,“马”的本质昭然若揭.
推论3 若随机变量ξ的分布函数F(x)在R上连续,则F(x)是唯一的.
证由推论1,当F(x)在R上连续时,∀x∈R,P{ξ=x}=0.现假设ξ还有另一个分布函数G(x),则由定理2知,∃λ,λ′∈R,λ≠λ′,有

综上,能实现概率分布的实函数F(x)区别于其它实函数的根本特征在于:它(们)是定义在R上的非负、规范、单调不减、在有间断点时可修改定义使其至少单侧连续的函数.
3.2 分布函数族及其形式统一性.
运用实分析理论,可得到分布函数被称为Lebesgue分解的一个结构[4],在那里,任何分布函数都可由三种基元函数(离散型分布函数、连续型分布函数和奇异型分布函数)迭加而成.这是一种分析结构意义下的分解.
我们当然也可在代数结构意义下剖析概率分布函数的结构.根据定理2和引言中的两型定义,可得出如下关系式:

这里,当在F(x)的连续点时,λ∈R,当在F(x)的间断点时,λ∈[0,1].可见定义1下的分布函数恰好是引言中两型分布函数的线性组合.这表明能实现概率分布的实函数自成一族,它们有着较好的形式统一性.
至于分布函数族中λ的实际意义,我们以一个实例加以说明.

3.3 两型分布函数定义的合理性.
下面从分布函数族出发,对引言中两型定义的合理性进行讨论.
定理3 在分布函数族F(x)=λF1(x)+(1-λ)F2(x)中,对于给定的x,F1(x),F2(x)线性相关的充分必要条件是F(x)的跃度为0.
证必要性.由F1(x),F2(x)线性相关,有F1(x)=kF2(x)(k≠0),于是

注意到F(+∞)=1,F2(+∞)=1,故有1=λk+1-λ,所以k=1.从而F1(x)=F(x)=F2(x) ,即F(x-0)=F(x)=F(x+0),故F(x)在x点处连续.由推论3知,P{ξ=x}=0.
充分性.显然,当P{ξ=x}=0时,有F(x-0)=F(x)=F(x+0),即F1(x)=F2(x),所以F1(x),F2(x)线性相关.
此定理表明,分布函数族中的所有分布函数在连续点处的解析表达是同一的,而在不连续点处,则根据跃度定义和借助单侧极限手段,可将整个分布函数族表达为如下形式:

可见,对整个分布函数族而言,F1(x),F2(x)各自都具有基元特征,因而从概率分布实函数实现的角度看,概率论中所给出的两型分布函数定义是有着深刻的合理性的.
4 结束语
分布函数概念是概率论中一个十分重要的概念.尽管实分析理论已给出了一般测度意义下分布函数的特征,但对概率测度来说,多少显得有些粗略,缺乏应有的完备性.本文基于一维随机变量,系统地阐释了概率分布实函数实现的内在本质,并通过这种阐释,还原了现有概率论中不曾讨论的分布函数族及其内在结构,并通过这种还原,揭示出概率论所给分布函数定义所蕴含的合理性和深刻性,这对完整理解分布函数概念,无疑地具有积极意义.
[1] 江泽坚,吴智权.实变函数论[M].北京:人民教育出版社,1979.
[2] 程其襄,张奠宙,魏国强,胡善文,王漱石.实变函数与泛函分析基础[M].北京:高等教育出版社,2003.
[3] 陶应奇.两种分布函数的比较[J].绵阳师范高等专科学校学报,1999,18(2):18-19.
[4] 应坚刚,何萍.概率论[M].上海:复旦大学出版社,2006.
The Question on the Real Function Realization of Probability Distribution
YI L i-ya
(The People’s Armed College,Guizhou University,Guiyang 550025,China)
Based on one-dimensional random variables,the writer gives a sufficient and necessary condition on the real function realization of probability distribution,obtains the family and continuity characteristic of the distribution function, and reveals the rationality and profundity of the definition of the distribution function in probability theory through explaining the intrinsic nature of the real function realization of probability distribution.
probability theory;real function realization of probability distribution;family of the distribution function;continuity
O211.1
A
1672-1454(2011)03-0139-06
2008-05-16
