连续模糊数OWA算子在物流选址中的运用

王爱玲

(菏泽学院数学系,山东菏泽 274015)

连续模糊数OWA算子在物流选址中的运用

王爱玲

(菏泽学院数学系,山东菏泽 274015)

物流中心的分布对现代物流活动有很大的影响,物流中心合理的选址能够减少货物运输费用,大大降低运营成本,从而提高企业竞争力.本文在连续模糊有序加权算子的基础上,提出一种新的处理模糊数据信息方法,同时在专家权重无法确定的情况下,建立了一种新的基于离差最小的目标规划模型来集结专家群体的不同偏好,并将其运用在物流选址中,该方法避免了模糊数的运算和比较,最后实例说明该方法在物流中心选址中的可行性.

模糊数;群决策;物流选址;FC-OWA算子

随着信息技术和现代管理理论的发展,物流研究在企业和社会都得到越来越多的重视,研究的内容主要包括单一配送中心选址方法和多个配送中心选址及分配方法两个方面[1],但综合起来主要还是关于物流中心如何选址的问题.选择合理的配送中心地址可以有效的节约费用,促进生产和消费两种流量的协调和配合,保证物流系统的高效和平衡发展.

物流中心选址主要是在一个具有若干供应网点及若干需求网点的经济区域内,选择一个或是多个地址作为物流中心的规划过程.物流中心涉及到多种设备以及建筑物,如果选址不当将造成长远的影响,为了使得最终所选择的物流中心是最佳位置,便需要综合考虑物流选址原则(包括适应性原则、协调性原则、经济性原则和战略性原则)和影响因素(包括自然环境因素,经营环境因素,基础设施状况等),对各个候选点进行分析、比较和评价,从而最终选择最优的地址建立物流中心[1,2].物流配送中心选址研究已经很多方法,大致可以分为定性和定量两大类.定量的方法主要包括重心法,运输规划法, Cluster法,CFLP法等;定性的则有层次分析法,多属性决策法[3,4].考虑到物流中心评价数据主要来自于过去的经验和决策者的主观判断,运用模糊数能更好的反应出信息评价过程中人思维和意识的模糊性和不确定性,故基于模糊数学的不确定决策方法得到了很大的发展和应用[3-7],本文在连续模糊有序加权算子的基础上,提出一种新的处理模糊数据信息方法,同时考虑到在群组决策过程中,会出现专家权重无法确定的情况,为此建立了一种新的基于离差最小的目标规划模型来集结群体的不同偏好,并将其运用在物流选址中,该方法避免了模糊数的运算和比较,最后实例说明该方法在物流中心选址中的运用.

1 基础知识介绍

定义1[7]实数域R上的模糊数具有隶属函数

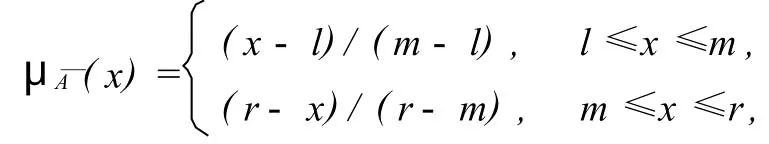
则称￣A为三角模糊数.三角模糊数￣A被简记为￣A=(l,m,r),当l=m=r三角模糊数退化为普通实数.

定义2[8-9]设为模糊数,且区间数[,]为模糊数˜a的α-截集.

其中ρ∶[0,1]→[0,1]具有下列性质的函数:

i)ρ(0)=0;ρ(1)=1; ii)若x＞y,ρ(x)≥ρ(y),

则称Ff为连续模糊数据OWA算子,简称FC-OWA算子.ρ称为基本的单位区间单调函数.

2 基于FC-OWA算子的物流中心选址的群决策模型

设某物流公司为了扩大业务,准备在全国各个城市选择几个城市中建立物流中心,经过前期的市场调查和分析,大致确定了n个城市(X)作为建立物流中心的候选城市.根据本公司运送物资的实际需要,通过分析,选择m个评价指标(G)来对这n个城市进行评价,为了提高决策水平与效率,避免因单个决策者的失误而导致错误决策、造成不良后果,聘请相关专业和相关领域的专家、学者与决策者组成的专家组(D)对这n个城市进行评价.为了更贴近客观情况,各专家选择模糊语言作为评价标度.

其中模糊语言对应着相应的模糊三角数:极好=(0.8,0.9,1),很好=(0.7,0.8,0.9),好=(0.6, 0.7,0.8),较好=(0.5,0.6,0.7),一般=(0.4,0.5,0.6),较差=(0.3,0.4,0.5),差=(0.2,0.3,0.4),很差=(0.1,0.2,0.3),极差=(0,0.1,0.2).各评价指标(G)的权重为w=(w1,…,wm).

物流中心选址的群决策决策过程:

(i)各专家运用模糊语言对各个城市的各个评价指标进行评价,得到评价矩阵.设第k个专家的模糊语言评价矩阵所选择评价指标的权重为w=(w1,…,wm)T.

(ii)将模糊语言标度转化成模糊三角数,再选取适当的参数λ,运用FC-OWA算子将所有模糊数转化成实数得到第k个专家的评价实数型决策矩阵

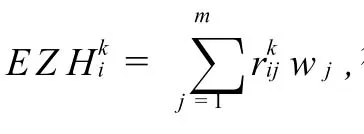
(iv)在集结群组意见的时候,仅将成员当成信息的提供者,不去考虑若计算的评价值与某个决策成员偏好值相差较大时,会遭到该决策成员极力反对,使该评价值无法得到认可,为了避免以上的情形,考虑到各专家权重未知,且要求最终集结的评价值要与各专家的意见偏差不大,只需要各专家对各个城市的评价值与群组意见的评价值偏差和最小,建立如下的群组专家信息集结模型:

综上所述,得到基于FC-OWA算子群决策确定各物流中心排序权重的模型为

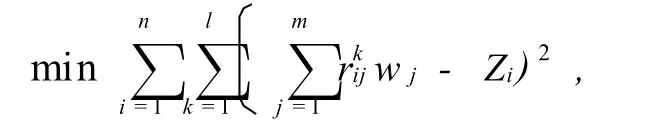
wj是第j个评价指标的权重;

Zi为所求各物流中心的排序权重值.

运用该模型,可以得到最后的群组专家决策意见,即最后各物流中心的排序权重Z=(Z1,…,Zn),再按照Zi的大小来确定最终建立物流中心的城市.

该模型是一个无约束最优化模型,运用MA TLAB中的求最优化函数fmins即可将最终的各物流中心的排序权值Z=(Z1,…,Zn)求解出来,fims为求多变量最小值的函数,其调用格式为x=fmins(‘F’,x0);其中F为需要最小化的目标函数,且F(x)应为向量变量的数值函数,x0为初始值.在对该模型求解过程中,最小化目标函数就是

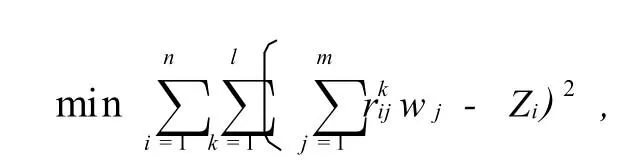
其中Z=(Z1,…,Zn)为自变量,初始值可以设为所有专家评价值的最小值就可以了.

3 实例分析

某企业为了扩大市场,欲选择两个城市建立物流中心,经过前期的调查,他们已经确定了四个候选城市xi(i=1,2,3,4);为了选出更适合企业未来发展的城市建立物流中心,该企业从自然环境G1、交通运输G2、经营环境G3、地理条件G4和公共设施G5五个方面综合考虑,聘请三位专家dk(k=1,2,3)组成委员会确定出最好的两个城市建立物流中心.三位专家dk(k=1,2,3)选用模糊语言标度对每个候选城市的各项指标进行评估,得到如表所给的评估信息.其中各评价指标Gi的权重w=(0.15,0.35,0.2, 0.2,0.1).

对于各专家对各城市的各项指标的评价信息运用FC-OWA算子(取ρ(y)=y3)经行处理得到如下的矩阵:

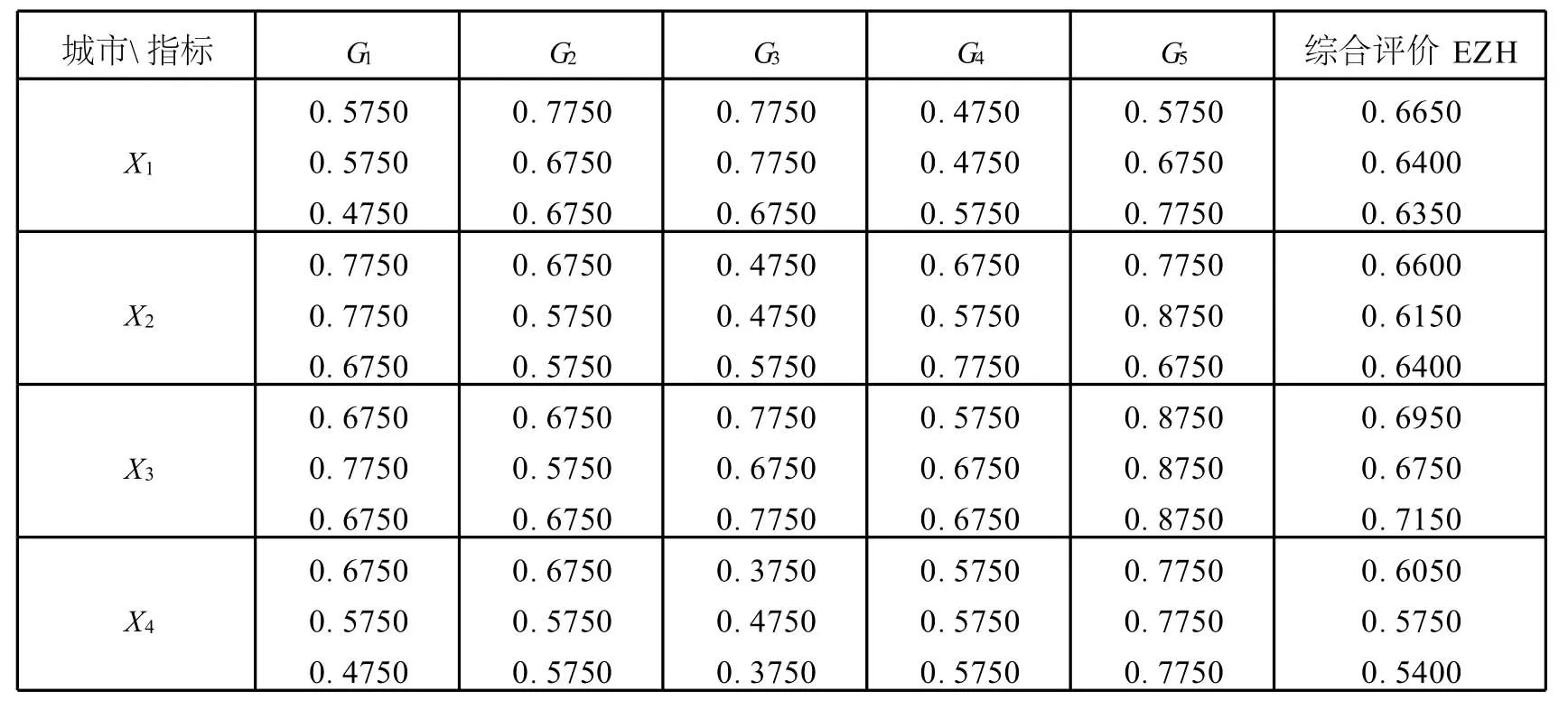
先将各城市各指标加权得到第k个专家对第i个城市的综合评价值EZ Hki如上表最后一列.考虑到各专家权重未知,为了能够使得最终集结到的专家群组决策信息符合各专家的偏好,运用模型

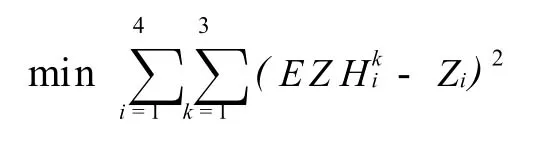
计算得到各城市的最终排序权重如下:

比较上面的综合值Zi,可以看出四个候选城市的排列顺序为x3≻x1≻x2≻x4,第三个城市的综合评价权重最高,表现比较突出,第一个和第二个城市的综合评分相差不大,而第四个城市的总体评价则最低,和第三个城市的综合评价值少了0.12还多,故该企业应该在x3,x1这两个城市建立物流中心.

在现有的物流选址中关于各物流备选城市的确定,最早的发展是凭领导人的主观意愿而确定的,随着科技的发展以及物流运输中各种资源消耗量的比较,使得各企业逐渐认识到利用科学的方法来确定物流配送中心的重要性,从而多属性群决策引入到了物流选址的确定中,关于多属性群决策,最早都是在选择了确定的指标后,通过对实际数据的统计以及关于专家组的咨询,得到一些决策信息,这些信息都是以实数的形式表示出来的.但是人的意识具有随机性和不确定性,往往用实数来刻画某一个属性是不符合现实的,而模糊数正好能刻画出人的意识的不确定性和随机性,从而用模糊数来刻画属性值更客观,更符合现实生活中的需要.虽然模糊数学在多属性决策中有所运用,但是模糊数的运算,以及模糊数的大小比较是一个难点,比较复杂,所以关于模糊数的去模糊是一个首先要解决的问题,本文刚好提出了一个去模糊数的有效方法,不仅避免了模糊数的运算和比较,也简化了运算.

4 结 语

在物流中心的选址规划中,对物流中心的选址原则、影响因素等进行综合分析,并提出缜密的决策建议是非常必要的.物流配送中心合理选址是一个重要而复杂的问题,在决策过程中,应充分考虑自然环境、交通运输、经营环境、地理条件和公共设施等因素的不确定性,运用系统工程的理论及方法对物流配送中心的设置位置进行研究和设计.本文在定性讨论物流选址的方法中,主要讨论了各评价信息是模糊数情况下的决策过程,并给出了简单易行的决策方法,使用本方法处理决策信息,既考虑到了实际评价过程中存在不确定性和模糊性的客观情况,又避免了决策过程中对模糊数据运算和排序容易出现序逆转的问题,还简化了决策过程中对数据的处理难度.

同时本文所给出的模糊群决策方法也可以运用到社会经济和生产过程的其它决策问题中.

[1] 李延晖,马士华,刘黎明.基于时间约束的多源多品种配送系统模型及一种启发式算法[J],系统工程理论方法应用,2004,13(5)：395-399.

[2]韩世莲,李旭宏,刘新旺,毛海军.多人多准则模糊层次分析法的物流中心综合评价优选模型[J],系统工程理论与实践,2004(7)：128-134.

[3]Chian-Son Yu,Chien-Kuo Li.A group decision making fuzzy AHP model and its application to a plant location selection problem[C]∥Joint 9th IFSA World Congress and 20th NAFIPS International Conference,Vancouver, Canada,2001：76-80.

[4]Chen-Tung Chen.Extensions of the TOPSIS for group decision making under fuzzy environment[J].Fuzzy sets and Systems,2000,114：1-9.

[5]刘开元,王蓉,金宝辉.一种供应商的模糊评价模型及其实现[J],武汉理工大学学报(交通科学与工程版),2004, 28(3)：.

[6]徐泽水.不确定多属性决策方法及应用[M].北京：清华大学出版社,2004.

[7] Michael Angelo B Promentilla,T Furuichi,K Ishhii,N Tanikawa.A Fuzzy Aralytic Network Process for Multi-Criteria Evaluation of Contaminated Site Remedial Countermeasures[J].Journal of Environmental Management, 2008,88(3)：479-495.

[8] Yager R R.OWA Aggregation Over acontinuous Interval Argument with Applications to Decision Making[J]. IEEE Trans.on Systems,Man,and Cybernetics-Part B,2004,34(5)：1952-1963.

Application of Continuous Fuzzy Number OW A Operator in Logistics Location

WA N G Ai-ling
(Department of Mathematics,Heze University,Heze,Shandong 274015,China)

Distribution of logistics has great impact on the modern logistics activities.Rational location of logistics centers can significantly reduce the transportation and operation costs,and thus improve competitiveness of the enterprises.In this paper,a new method for dealing with fuzy data information is put forward based on the continuous fuzzy ordered weighted operator.Under the case with uncertain expert weights,a new goal programming model to gather the different preferences of experts based on the minimum deviation is developed,and then is applied to the site selection for logistics.The method presented in the model can avoid the ocmputation and comparison of fuzy numbers.Finally, some examples are given to illustrate the feasibility of the method on the location of logistics centers.

fuzzy number;group decision-making;logistics location;FC-OWA operator

O159

A

1672-1454(2011)03-0134-05

2009-10-10