两两独立序列加权和的Lr收敛性

李 炜, 柳向东

(1.仲恺农业技术学院计算科学学院,广州 510225; 2.暨南大学经济学院统计学系,广州 510630)

两两独立序列加权和的Lr收敛性

李 炜1, 柳向东2

(1.仲恺农业技术学院计算科学学院,广州 510225; 2.暨南大学经济学院统计学系,广州 510630)

讨论了两两独立随机变量列加权和在满足r(1≤r＜2)阶Ces‘aro一致可积条件下的Lr收敛性,获得了与独立情形一致的结果.用相似的方法,对于其它相依或混合序列(如两两NQD列,φ-混合序列, ρ-混合序列)也有相同的结果.

两两独立;Lr收敛性;Ces‘aro一致可积

1 引 言

Pyke和Root[1]曾经证明,对于独立同分布的随机变量序列{X,Xn,n≥1},如果0＜r＜2,E|X|r＜∞,则有下面的Lr收敛性结果

其中如果0＜r＜1,则b=0;如果1≤r＜2,则b=EX.这个结果已经被推广到了不同的情形,如当1≤r＜2时推广到独立但不一定同布情形以及鞅差序列情形;当0＜r＜1时推广到任意随机变量序列情形,当然其中的条件E|X|r＜∞被换成更广泛的r阶Ces‘aro一致可积的条件(见文[2],等).无论是在独立情形还是鞅差序列情形下,其证明的关键是用到了下面的Marcinkiwicz-Zygmund不等式

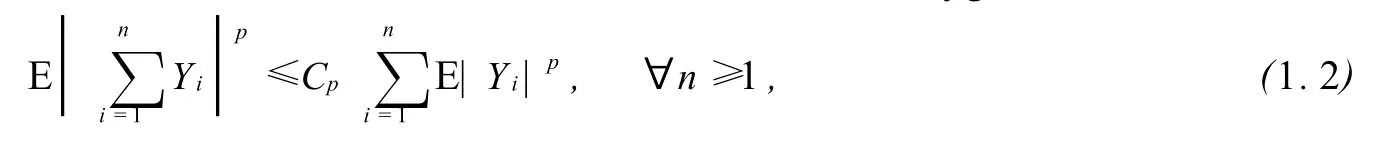
其中{Yn,n≥1}是均值为0的独立或鞅差随机变量序列,1＜p≤2,常数Cp＞0只与p有关.

但对于非独立情形的随机变量序列,如两两独立序列,两两NQD列,φ-混合序列,ρ-混合序列, (1.2)式对于1＜p＜2是否成立至今仍然没有解决,因此要对这些序列得到同样的结果是不能再用独立或鞅差情形时的方法的,而必须寻找新的方法.本文的目的就是用新的方法不但把(1.1)式完全推广到了这些序列,而且还在更广泛的条件下,即不一定同分布但在r阶Ces‘aro一致可积条件下及加权情形下得到与独立情形完全一致结果,当然Pyke和Root[1]的结果作为其推论了.

先来介绍一些概念.

设{Yn,n≥1}是随机变量序列,p＞0,∀n≥1,E|Yn|p＜∞.若

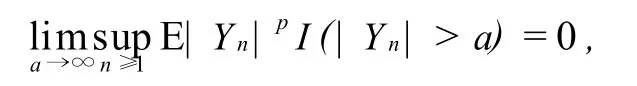
则称{Yn,n≥1}是p阶一致可积的;若

则称{Yn,n≥1}是p阶Ces‘aro一致可积的.很明显一致可积蕴含Ces‘aro一致可积,但文献[3]指出Ces‘aro一致可积严格弱于一致可积.

本文总设C代表正常数,在不同的地方可以代表不同的值.

2 主要结论及证明

下面就给出本文的主要结果及其证明.

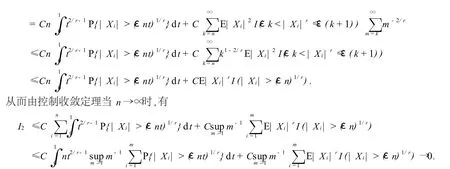
由定理2.1立即有下面的推论.

推论2.1 设{X,Xn,n≥1}是同分布的两两独立随机变量序列.设1≤r＜2.若E|X|r＜∞,则(1.1)成立.

注1 定理的证明本质上用到了当p=2时的不等式(1.2).对于两两NQD列,φ-混合序列,ρ-混合序列等在适当的条件下(1.2)对p=2也是成立的,因此定理2.1及推论2.1亦成立.

注2 万成高[4]也讨论了两两NQD列的Lr收敛性,但他的结果是在2阶Ces‘aro一致可积条件下获得的,因而他的结果不能完全推广Pyke和Root[1]结果.而本文的定理2.1是在与独立情形相同的条件下得同样的结果(独立情形的结果可见文[2]),从而可以完全推广Pyke和Root[1]结果,即得到本文的推论2.1.

[1] Pyke R,Root D.On convergence inr-mean of normalized partial sums[J].Ann Math Statist,1968,32(9)：379-381.

[2] Chen P Y,Liu J J,Gan S X.Convergence forBvalued random fields and the type of abanach space[J].J Wuhan Univ(Natural Science Edition),1998,44(1)：11-14.

[3] Chandra T K.Uniform integrability in the Ces‘aro sence and the weak law of large number[J].Sankhya：the Indian J of Statist(Sr A),1989,51(2)：309-317.

[4] Wan C G.Law of large numbers and complete convegence for pairwise NQD random sequeces[J].Acta Math Appl Sinica,2005,28(2)：253-261(in Chinese).

LrConvegence for Pairwise Independent Random Variables

L I Wei1, L IU Xiang-dong2
(1.Department of Computation Science,Zhongkai University of Agriculture and Technology,Guangzhou 510225,China; 2.Department of Statistics,Jinan University,Guangzhou 510630,China)

The author discusses theLrconvergence for the weighted sums of pairwise independent random variables underr-th Ces‘aro uniform integrability,which is the same as that in the independent case.By the similar argument,the result is also ture for the other dependent random variables(such as pairwise NQD,φ-mixing,ρ-mixing).

pairwise independent;Lrconvergence;Ces‘aro uniform integrability

O211

A

1672-1454(2011)03-0131-03

2008-06-03