自共轭常微分方程边值问题与变分问题的等价性

夏必腊, 王金山

(解放军炮兵学院数学教研室,合肥 230031)

自共轭常微分方程边值问题与变分问题的等价性

夏必腊, 王金山

(解放军炮兵学院数学教研室,合肥 230031)

首先给出了自共轭常微分方程及其边值问题,进而证明了自共轭常微分方程边值问题等价于一个泛函变分的极值问题,最后指出了将自共轭常微分方程边值问题转换为等价的泛函变分极值问题的好处.

共轭;常微分方程;边值问题;变分;极值;等价

1 自共轭常微分方程及其边值问题

形如

的微分方程称为自共轭常微分方程,其中pk(x)∈Ck[x0,x1]且pk(x)至多只有有限个零点.方程(1)是一个2n阶微分方程,是函数论中一个很重要的方程,许多著名方程都可由它派生出来.特别,当n=1时,方程(1)变为

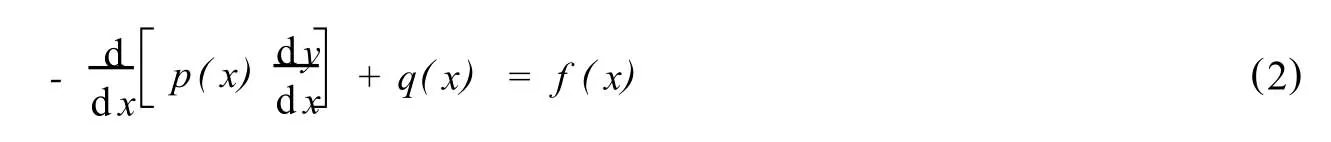
是一2阶微分方程,其中p(x)≥0和q(x)≥0且均为连续函数,p(x)至多只有有限个零点.方程(2)的边界条件为

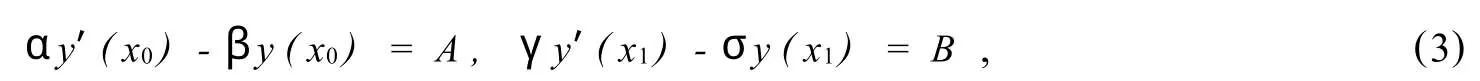
其中α,β,γ和σ为常数且非负,A,B为常数,α2+β2≠0,γ2+σ2≠0.当α≠0,γ≠0时,β2+σ2≠0.

2 微分算子及性质

下面讨论算子T的性质.据式(3),设α≠0,γ≠0,利用分部积分法,有

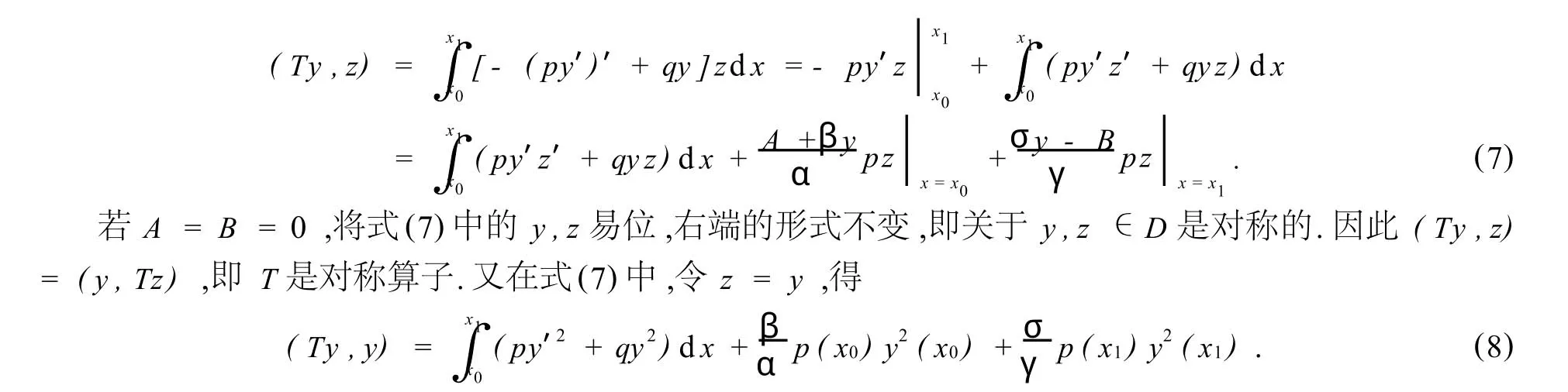
根据假定p(x)≥0,q(x)≥0,α,β,γ和σ非负,因此(Ty,y)≥0,即T是正定算子.

式(7)和式(8)是在α≠0,γ≠0的条件下得到的.若α=γ=0,则这两式中含有α和γ的项不出现,此时无论A和B是否为零,T都是对称正定算子.

综上所述,当A=B=0或α=γ=0时,问题给定的自共轭微分算子T是对称正定算子.

3 与自共轭常微分方程边值问题等价的变分问题

由此可见,在α≠0和γ≠0的边界条件下,式(12)的一阶变分为零,二阶变分不小于零,即式(12)取得绝对极小值的充分条件为y=y(x)是方程(2)的解,故式(12)就是所求的泛函.

当α=γ=0时,边界条件可简化为

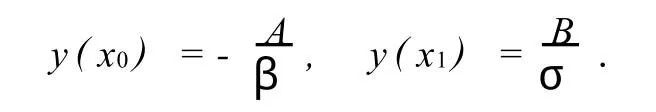
此时y(x0)和y(x1)都是常数,即边界条件都固定,有δy(x0)=δy(x1)=0.对泛函(12)取一阶和二阶变分,仍是(10)和(11),但由于δy(x0)=δy(x1)=0,一阶变分中的2py′δy=0.由此可见,在上述边界条件下,泛函(9)的一阶变分为零,二阶变分不小于零,即泛函式(9)取得绝对极小值时的充分条件为y=y(x)是方程(2)的解,故式(9)就是所求的泛函.然而,比较式(9)和式(12)可以看出,将(12)中有关α和γ的项去掉,则式(12)就可退化为式(9).类似地,如果在边界条件(3)中有某常数为零,则在式(12)中去掉与该常数有关的项后所得到的泛函就是与方程(2)的解对应的泛函.于是,可得到下面的定理：

定理设y∈C2[x0,x1],y=y(x)是微分方程(2)在边界条件(3)下的解的充要条件为它对应的泛函(12)在y=y(x)处取得绝对极小值,且边界条件(3)中的与常数α,β,γ,σ,A和B相关的项和泛函(12)中的同名常数相关的项相一致.

4 推 广

有时还会遇到非自共轭微分方程,在某些情况下,用一个待定因子μ(x)乘以该方程,可使它化为自共轭微分方程.例如：二阶线性微分方程

5 实 例

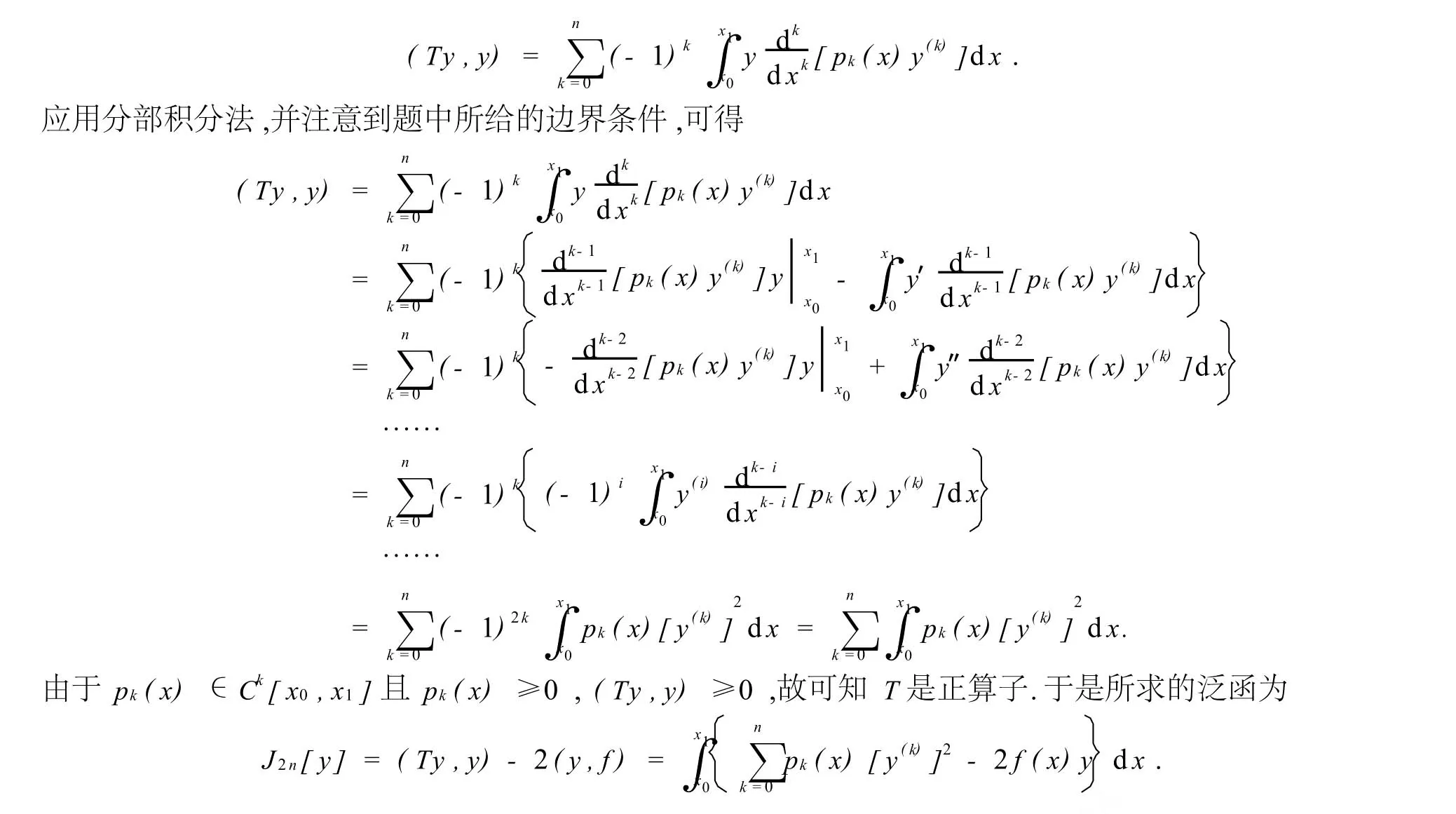
[1] 艾利斯哥尔兹.变分法[M].北京：高等教育出版社,1983.

[2] 钱伟长.变分法及有限元讲义[M].北京：高等教育出版社,1987.

[3] 老大中.变分法基础[M].北京：国防工业出版社,2003.

[4] 柯朗·希尔伯特.数学物理方法[M].北京：高等教育出版社,1988.

Variation Problemof Equivalence with Boundary Value Problem of Self Conjugate Ordinary Differential Equation

X Iabi-la, WA N G J in-shan
(Teaching and Research Section of Math.,PLA Artillery Academy,Hefei 230031,China)

This paper presents with boundary value problem of self conjugate ordinary differential Equation first,then proves that the Equation with boundary value problem and variation problem are equivalent,and finally gives the advantages of this kind of transformation.

conjugate;ordinary differentialEquation;boundary value problem;variation;extreme value; equivalence

O175.8

A

1672-1454(2011)03-0120-04

2008-03-27