双障碍幂型期权定价公式

孙江洁, 杜雪樵

(合肥工业大学数学学院,合肥 230009)

双障碍幂型期权定价公式

孙江洁, 杜雪樵

(合肥工业大学数学学院,合肥 230009)

为了进一步完善障碍期权理论,更好地适应金融市场的需求,本文在完全市场条件下,利用连续时间的双障碍幂型期权买权过程的鞅性和等价鞅测度变换的方法,得到了双障碍幂型期权定价模型的显式解.

双障碍期权;幂型期权;鞅;停时;买权

1 引 言

近年来,国际金融市场上除了欧式和美式期权外,还涌现出大量由标准期权变化、组合和派生的新品种,即新型期权[1].它是通过改变股票结构,使股票价格变化依赖于股票价格路径一种奇异期权.我们都知道,标准的欧式看涨(看跌)期权的支付函数均为股价的线性函数.但在金融工程事务及理论领域存在如下形式的支付函数:max{SαT-K,0},在这里,α＞0,为常数,K为执行价格,T为到期日,记幂函数SαT=(ST)α,设此幂函数为非负单增函数,它改变了股票价格的变化路径,它是新型期权的一种.因为它是依赖股票价格的幂型函数变化路径,所以它对股票价格变化的敏感性明显增强,为了满足部分投资者的喜好,为了尽可能避免少数投机者操纵投资市场,我们有必要对障碍期权和障碍幂型期权进行研究.如Merton(1973)[2]和Goldman et al(1979)[3]对单障碍期权进行了探索,2004年,李霞、金治明讨论了障碍期权的定价问题[4].然而,对单障碍期权的自然推广则是双障碍期权的定价问题.于是,在2004年,张斌、韩萍利用鞅的方法讨论了双障碍期权定价问题[5];在2005年,李小爱对障碍平方期权进行了研究[6].同年,肖艳清、邹捷中等得到了下降敲出的指数屏障期权定价公式[7].本文在这里主要研究了完全市场条件下,双障碍幂型期权的定价公式.

2 金融市场的描述

假定市场是完全、无套利的,只有风险资产St和无风险资产p(t),其价值过程{St∶t≥0}和{p(t)∶t≥0}满足如下微分方程:

这里{Bt}t≥0是带σ-代数流的概率空间(Ω,F,{Ft}t≥0,P)上的标准布朗运动.μ,σ,r分别是股票瞬时期望受益率和波动率及无风险利率,且均为固定常数.令

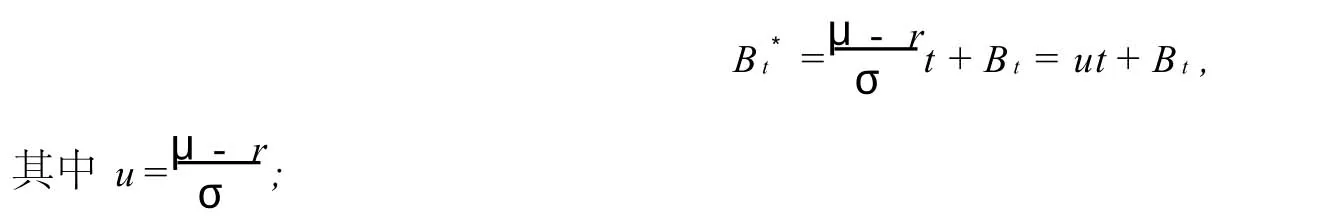
由测度变换的Girsanov定理容易得到P＊为风险中性测度,且B＊t为P＊下的布朗运动.

引进记号:下障碍水平为L,(L＞0且L＜Sα0);上障碍水平为H,(H＞Sα0),假定H＞K,令

下面我们讨论双障碍幂型买权在到期日T的价值:

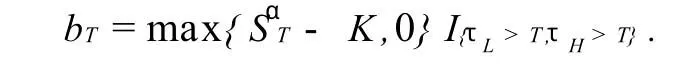
3 双障碍幂型期权定价公式

定理在上述的条件下,双障碍幂型看涨期权在到期日的价值为

在证明定理之前,先给出两个引理:

引理1[5]各种假设和定义同上,如果风险资产St满足(1)式,且支付函数为幂型函数时,双障碍幂型期权买权贴现到0时刻的价值过程:{Cα(St∧τL∧τH,,t∧τL∧τH),0≤t≤T}是一个鞅.这里t∧τL∧τH≜min{t∧τL∧τH}.

引理2[8]J是[a,b]的一个Borel子集,对于a＜0＜b,取c=b-a,有

定理的证明 由引理1可知,双障碍幂型看涨期权在到期日的价值为

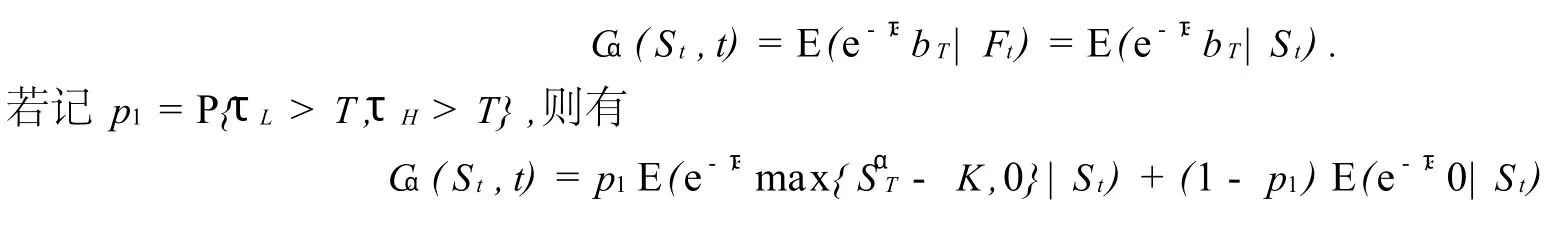
4 结束语

本文主要探讨了双障碍幂型期权的定价问题,并得到了在完全市场条件下,双障碍幂型期权的定价公式.它进一步推广了文献[2-7]的结论.在一般市场上,情况比较复杂,有待进一步研究.

[1] 吴素琴,杜雪樵.上升敲出障碍期权二项式定价模型[J].合肥工业大学学报(自然科学版),2006,29(5)：500-502.

[2] Merton R.Theory of Rational option Pricing[J].Econ.Manag.Sci(Spring),1973,4(1)：141-183.

[3] G oldman M,Sosin H,Gatto M.Path dependent options：buy at the low,sell at the high[J].Finance,1979,34(12)：111-127.

[4] 李霞,金治明.障碍期权的定价问题[J].经济数学,2004,21(3)：200-208.

[5] 张斌,韩萍.双障碍期权的数学模型及其定价[J].新疆师范大学学报,2004,23(4)：36-40.

[6] 李小爱.障碍平方期权的定价[J].数学理论与应用,2005,25(2)：61-64.

[7] 肖艳清,邹捷中.指数屏障期权定价模型[J].经济数学,2005,22(4)：368-372.

[8] David A.Freedman.Brownian motion and diffusion[M].London：Cambridge university press,1970：31-37.

[9] Musiela M,Rutkowski M.Martingale methods in finanmcial modelling[M].New York：Springer-Verlag,2003：110-116.

The Pricing of Double-barrier Power

SUN J iang-jie, DU X ue-qiao
(School of Mathematics,Hefei University of Technology,Hefei 230009,China)

It is proved the pricing formulas of double-barrier power options.By double-barrier buy power options is a martingale and means of martingale method in the complete market.It is further to improve the theory of barrier options to adapt the need of financial market.

double-barrier options;power option;martingale;stopping-time;Buy-option

O211.62

A

1672-1454(2011)03-0115-05

2008-02-25