T(2,2,n)∪(Ci)的匹配等价图类

詹福琴, 乔友付

(河池学院数学系,广西宜州 546300)

詹福琴, 乔友付

(河池学院数学系,广西宜州 546300)

利用图的匹配多项式及其最大实数根的性质完整刻画了T(2,2,n)∪(Ci)(n≥3,A是大于等于3的整数组成的可重集)的匹配等价图类.

匹配多项式;匹配等价;匹配唯一;最大实数根

1 引 言

本文仅考虑有限,无向简单图.设G是有n个顶点的图,V(G),E(G)分别表示G的顶点集和边集. G的一个匹配是指G的一个生成子图,它的每个分支或是孤立点或是孤立边.t-匹配是指其中有t条边的匹配.文[1]定义图G的匹配多项式为

其中at(G)是G的t-匹配的数目.两个图G和H,若有μ(G,x)=μ(H,x),则称G和H匹配等价,记为G～H.若与图G匹配等价的任何图H,均有G≅H,则称图G是匹配唯一的.Φ(G,x) =det(λI-A(G))表示图G的特征多项式.其中A(G)表示图G的邻接矩阵,λ1(G)表示Φ(G,x)的最大特征根.M(G,x)表示图G匹配多项式μ(G,x)的最大实数根.

Pn,Cn分别表示有n个点的路和圈;Q(s,t)(s≥2,t≥1)表示圈Cs+1上的一点与路Pt+1的一个端点粘接后得到的图;T(a,b,c)表示从一点引出三条长分别为a,b,c(a≤b≤c)的路得到的图; T(a,b,n,c,d)表示从路Pn+1的两个1度点分别引出长为a,b和c,d的路得到的图,特别地,当a=b=c=d=1时,该图表示为Un(n≥6);¯G表示图G的补图.

为方便,用μ(G)表示μ(G,x);M(G)表示M(G,x).文中其他未特别说明的概念和术语均参见[1-2].

2 基本定义和引理

引理1[1]设图G有k个连通分支：G1,G2,…,Gk,则

引理2[1]设e=uv是图G的一条边,则μ(G,x)=μ(G-e,x)-μ(G-{u,v},x),这里G-e, G-{u,v}分别表示从G中删去边e,顶点u,v后得到的图.

引理3[1]设u∈V(G),e∈E(G),且G连通,则M(G)＞M(G-u);M(G)＞M(G-e).

引理4[1]如果图G是一个森林,则μ(G,x)=Φ(G,x).

引理5 对任意的树T,则有M(T)=λ1(T).

证由引理4结论显然成立.

定义1[3]设图G的顶点序列为x1,x2,…,xk,若满足：

(i)除x1与xk有可能相同外,其余xi互不相同;

(ii)顶点度d(xi)满足d(x1)≥3,d(x2)=…=d(xk-1)=2(除非k=2),d(xk)≥3;

(iii)对于i=1,2,…,k-1,有xi与xi+1相邻,

则称x1,x2,…,xk是图G的一条内部路.

引理6[4]设Gxy是由剖分G中的边xy得到的图,则有

(i)若xy不属于G的内部路,且G≠Cn,则λ1(Gxy)＞λ1(G);

(ii)若xy属于G的内部路,且G≠Un(n≥6),则λ1(Gxy)＜λ1(G).

引理7 设uv是树G的任意一条边,则

(i)若uv不属于G的内部路,则M(Guv)＞M(G);

(ii)若uv属于G的内部路,且G≠Un(n≥6),则M(Guv)＜M(G).

证由引理5,引理6可得结论成立.

引理8[5]若G是连通图,则

(i)M(G)＜2当且仅当G∈Ω1={K1,Pn,Cn,T(1,1,n),T(1,2,i)(2≤i≤4),Q(2,1)};

(ii)M(G)=2当且仅当G∈Ω2={K1,4,T(2,2,2),T(1,3,3),T(1,2,5),In,Q(2,2),Q(3,1)}.

引理9[6]设G是一连通图,则当且仅当G是下列图之一：

(i)T(a,b,c)其中a=1,b=2,c＞5或a=1,b＞2,c＞3或a=b=2,c＞2或a=2,b=c =3;

(ii)T(1,a,b,c,1)其中(a,b,c)∈{(1,1,2),(2,4,2),(2,5,3),(3,7,3),(3,8,4)}或a≥1, b≥b＊(a,c),c≥1,这里(a,c)≠(1,1)且

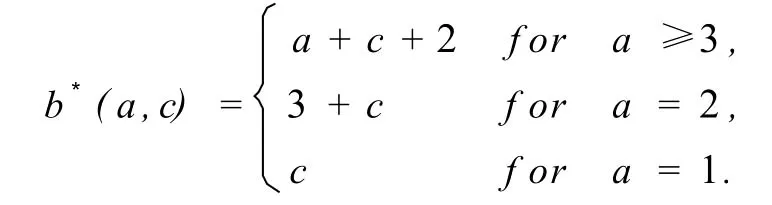
(iii)Q(2,n)(n≥3),或Q(m,1)(m≥4),或Q(3,2).

定义2[1]设G是一个连通图,u∈V(G),定义图G关于点u的路树T(G,u)如下：

V(T(G,u))={G中从点u开始的路(包括点u)};

E(T(G,u))={(P1,P2)|P1,P2是G中从点u开始的路,且一条路是另一条路的极大真子路}.

引理10[7]对任意连通图G,M(G)等于它的任意顶点路树的最大特征根.

引理11[8]图∪

i∈ACi是匹配唯一的,其中A是大于等于3的整数组成的可重集.

引理12[9]设G有n个顶点n-1条边,且G的度序列π(G)={1,1,1,3,2,…,2},如果μ(G,x)=μ(H,x),则H的度序列为π(H)={1,1,1,3,2,…,2},或π(H)={0,2,…,2}.

引理13[10]Q(m,n)～Q(n+1,m-1).

引理14[11](i)P2m+1～Pm∪Cm+1(m≥2);T(1,1,n)～K1∪Cn+2(n≥1);

(ii)若m+1=2n+1对某个正整数n成立,则此时Pm的所有匹配等价图是：

特别地,仅当m+1=3×2n-1时,Pm的匹配等价图才含有P2分支P2∪C3∪C6∪…∪C3×2n-2

证由引理15,比较各式两边匹配最大根可得结论成立.

3 主要结果及其证明

引理17 对任意正整数t≤n1,若max{b,d}≥t,则有M(T(1,t,n1))＜M(T(1,b,n2,d,1)).

证不妨设max{b,d}=b≥t,由引理3和引理7可得

[1] Godsil C D.Algebraic Combinatorics[M].New York：Chapman and Hall,1993.

[2] Bondy J A,Murty U S R.Graph Theory with Applications[M].North-Holland：Amsterdam,1976.

[3] Cvetkovic D,Rowlinson P.The largest eigenvalue of a graph：A survey[J].Linear and Multilinear Algebra,1990, 28(1,2)：3-33.

[4] Cvetkovic D M,Doob M,Gutman I,Torgaser A.Recent result in the theory of graph spectra[M].New York： Elsevier Science Publishers,1988.

[5] 马海成.匹配根对图的刻画[J].曲阜师范大学学报,2001,27(1)：33-36.

[7] 马海成,赵海兴.小度数或大度数图中的匹配唯一图[J].数学研究与评论,2004,24(2)：369-373.

[8] 郭知熠,俞玉森.关于两类图的匹配唯一性[J].应用数学,1989,2：25-32.

[9] 申世昌.T形树的匹配唯一性[J].数学研究,1999,32(1)：86-91.

[10] 李改杨.几类图的匹配唯一性[J].应用数学,1993,5(3)：53-59.

[11] 马海成.两类图的匹配等价类[J].数学研究,2000,33(2)：218-222.

[12] 张海良.几类图的匹配多项式之间的关系与一类图的匹配等价图[J].纯粹数学与应用数学,2007,23(2)：178-182.Ci)(n≥3 andAis multiset with integer numbers of more than or equal to 3 as its elements),by the properties of graph’s matching polynomial and it’s maximum roots.

On the Matching Equivalent Classes ofT(2,2,n)∪(Ci)

Z HA N Fu-qin, QIAO You-f u

(Department of Mathematics,Hechi University,Yizhou,Guangxi 546300,China)

matching polynomial;matching equivalence;matching uniqueness;the maximum real roots of graph’s matching polynomial

We completely characterize the matching equivalent classes ofT(2,2,n)∪(

O157.5

A

1672-1454(2011)03-0053-06

2008-08-21;[修改日期]2008-12-24

广西教育厅科研项目(201010LX471;201010LX495);河池学院科研项目(2009A-N004;2008QS-N007,N008)