假设检验在体育统计应用中应注意的两个问题

曹远红

（湖南师范大学 体育学院，湖南 长沙 410012）

假设检验在体育统计应用中应注意的两个问题

曹远红

（湖南师范大学 体育学院，湖南 长沙 410012）

现有的体育统计教材对假设检验的有关问题缺乏详尽的论述，文中以参数检验为例，对体育统计中假设检验的原理和方法进行了论述，特别是对假设检验中原假设的确立和假设检验中的两类错误的控制问题进行了深入的阐述，旨在为体育统计的教学和体育科研中假设检验的应用提供有益的参考。

体育统计；假设检验；参数检验；原假设

体育统计的学科体系已经基本成型,内容主要包括描述统计、假设检验、参数估计、相关分析、回归分析、方差分析、多元统计分析等[1]。全国绝大多数体育院系早已将体育统计作为本科必修课程。体育统计方法在体育实践中不断发展、提高和深化，随着近年来体育科技的飞速发展和体育科学化程度的迅速提高,体育统计的原理和方法已被体育界广泛接受。假设检验是统计推断中的重要内容，特别是参数检验在体育科研和体育实践中有着重要的作用，但目前我国体育院校所采用的体育统计教材对假设检验的原理和方法缺乏较详尽的论述，不利于体育统计的教学和假设检验在体育实践中的应用，在实际应用中容易出现错误。基于此，本文对假设检验中的原假设的确立问题和 的控制问题进行了论述。

1 假设检验的概念和原理

所谓假设检验就是对总体分布的参数或总体分布的性质提出某种假设，然后根据样本信息对提出的假设进行检验，判断该假设是否成立[2]。假设检验分为参数检验和非参数检验，前者是对总体分布的某个参数提出某种假设，利用来自总体的样本检验假设是否成立；后者是总体分布的性质提出假设，用来自总体的样本检验该假设是否成立。参数检验主要有U检验（也叫Z检验）、T检验、2χ检验等，非参数检验主要有秩和检验、符号检验等。

在参数检验中，原假设用0Η表示，与原假设相对立的是备择假设，用1Η表示。0Η的建立至关重要，因为假设检验是一种带有概率性质的反证法，其基本思想是小概率事件原理，即认为小概率事件在一次实验中是不会发生的。假设检验的过程实质上基于原假设的一种推理过程，先假设成立，从Η0出发推导，如果发生了小概率事件，认为Η0不真，则作出拒绝Η0的决定，反之，就没有理由拒绝Η0，从而接受Η0。其过程可以通俗地描述：“假设某一事实A成立，如果在A成立的基础上，某事件B发生的概率很小，在一次抽样中，B事件发生了，则认为事实A不成立，否则只能认为A事实成立。”

2 单侧、双侧检验的区分

在参数检验中，单、双侧检验的称呼主要是依据其拒绝域的形式来命名的，把拒绝域分布两侧的检验叫双侧检验，把拒绝域分布一侧的检验叫单侧检验[3]。在实际应用中到底用单侧检验还是用双侧检验，这需要根据我们的研究目的而确定，如果要检验某统计量是否来自某一总体，或者检验某一 值是否等于已知0值，这时的任务只需检验 是否等于0， ＞0或 ＜0都将拒绝原假设，所以双侧检验的拒绝域分布在两侧。至于谁大谁小我们是不需要考虑的，这种情况通常用双侧检验。在另外一些情况，我们要检验的问题带有方向性，即要检验某一 值是大于还是小于已知的 0值，这时需要采用单侧检验。单侧检验又分为左单侧检验和右单侧检验，又分别叫下限检验和上限检验[4]。在体育科研的实践中，往往是用单侧检验较多，比如说采用了某种新的训练方法成绩是否有提高，某地区青少年的平均身高是否有所增长，通过实验条件的改变，某指标是否变低还是变高等等，诸如此类的问题都是带有方向性，需要采用单侧检验。不管是单侧还是双侧检验，至于需要检验的 值都是不知道的，而是根据已有的样本信息对 值进行检验。

那么，拒绝域又如何确定呢？同样是依据小概率事件原理而确定的。下面以检验样本平均数是否来自已知总体平均数（且总体标准差 已知）为例来说明这个问题，取

=0.05，在双侧检验中，对于原假设0Η：＝0，备择假设Η1： ≠0，那么在原假设成立的基础上，对于X～N（0， ），则有，根据数据标准化，则～N（0，1），因为 =0.05，所以有95%的可能处于（-1.96，1.96）之间，同理，通过转换同样可知样本平均数x有95%的可能处于之间，而不在这个区间的概率仅为5%。如果落入这个区间之外则发生了小概率事件，就依据小概率事件原理认为样本平均数不是来自这个总体，从而拒绝原假设。因为在正态分布的钟形曲线中95%的区间处于中间，小概率处于两边，所以拒绝域分布于两侧，从而叫双侧检验。

单侧检验的拒绝域为什么只分布在一侧呢？以检验已知样本平均数x所在的总体平均数 是否大于已知总体平

均数0为例，如果原假设Η0： ＞0，Η1： ≤0，取 =0.05，同理，在原假设成立的基础上进行推导，如果原假设成立，那么从平均数为 的总体中随机抽取一个样本，则样本平均数落入左侧小概率区间的概率很小，因为在正态分布和t分布的图形中，我们知道左侧是小于平均值的区间，右侧是大于平均值的区间，也就是说：通过标准化后的U值落入（-∞，-1.65）的区间概率很小，因为Uα=1.65，则 U1−α=−1.65，如果落入这个区间，则发生了小概率事件，同理，依据小概率事件原理，就拒绝原假设，这时拒绝域只分布在一侧，因此叫单侧检验。反之，如果原假设0Η：＜0，则拒绝域分布于右侧，原理还是一样的。

3 原假设的确立

在上文中已提到假设检验是一种带有概率性质的反证法，假设检验的过程实质上基于原假设的一种推理过程，因此原假设的确立是假设检验的开始，原假设正确与否是假设检验的关键。为了更能说明这个问题，通过下面的实例来说明。

例：[5]已知在某运动饮料中，维生素C的含量服从正态分布，按规定，维生素C的含量不得低于21毫克。现在从一批饮料中抽取17罐，计算得知维生素C含量的平均值x=23毫克，S=3.09毫克，问该批饮料维生素C含量是否合格？（ =0.05）

在上述例题中，属于总体标准差未知且为小样本的检验，所以用t检验法，问题是维生素C含量是否合格，即是否大于21，属于单侧检验，那么原假设有两种情况， H0：

< 2 1（假设维生素C含量不合格）或 > 2 1（假设维生素C含量合格），因为查t值表可知， t0.05(16)=1.746。如果原假设是 H0： < 2 1，则拒绝域为:t≥ t0.05(16)=1.746，因为t=2.072>1.746，所以拒绝原假设，认为该批运动饮料维生素C含量合格；如果原假设是 H0： > 2 1，则拒绝域为:t≤ −t0.05(16)=−1.746,因为t=2.072>-1.746，所以接受原假设，认为该批运动饮料维生素C含量合格。

两种不同的原假设，得出一样的结论，两种方法是否都正确？检验的效果是否一样呢？要回答这些问题，还是要从假设检验的原理即小概率事件原理来阐述，假设检验中的显著性水平 实际上就是我们人为规定小概率事件的概率，当拒绝原假设时，我就有1- 的把握认为原假设为伪，如果接受原假设时，则只表明没有充足的理由证明原假设是错的，只能接受原假设；反过来也就是说要拒绝原假设则需要较充足的理由，接受原假设则是“被迫”接受。可见原假设往往是处于受保护地位的，一般是根据已有的知识和经验把不能轻易否定的东西作为原假设，比如在检验某产品的质量时，商家希望把“质量合格”作为原假设，因为这样容易得出接受原假设的结论，而要拒绝原假设是需要充足理由的。在体育科研的实践中往往将希望证实的反面作为原假设,将希望证实的问题作为备择假设，这样一旦拒绝原假设，不仅具有充足的理由，而且往往意味科研成功，符合科学研究要严谨的习惯。比如说要检验一种新的训练方法是否有效，就把新的训练方法无效作为原假设。于是，在上文中例题中，将 21< 作为原假设，方法更准确，结论也更有说服力。

4 两类错误的控制

假设检验的逻辑是概率反证法，但做检验时是根据抽样得到的样本值作出拒绝还是接受0Η的决定，由于样本具有随机性，假设检验有可能犯错误，这种错误分为“弃真”错误和“取伪”错误，也即“第一类错误”和“第二类错误”。假设检验中显著性水平 就是犯“弃真”错误的概率，“取伪”错误的概率用 表示。我们都希望在假设检验中这两类错误的概率越小越好，但对于一定的样本量，当 增加时， 减小，反之当 减小时，将导致 的增加。就像在区间估计中，要想增大估计的可靠性，就会使区间变宽而降低精度；要想提高精度就会要求估计区间变窄，从而使可靠性下降。也就是说，我们在实际操作中根本无法找到一个能使 与 同时减小的临界域，除非增大抽样容量，但是无限增大样本容量并非抽样的本意。还是以例题来说明这个问题。

某公司生产的体育用品, 根据以前资料可知平均使用寿命为1000小时,现欲采用新工艺生产, 在新工艺试用期从生产的用品中随机抽出25件,样本平均寿命为1040小时。已知总体标准差为100小时, 请在 =0.01的显著性水平下检验产品寿命是否有显著提高？

根据题中条件, 该问题属于小样本但总体标准差已知的检验, 采用U检验法。又因为问题是检验产品使用寿命是否有显著提高，所以属单侧检验。分别有如下两种:已知

0=1000， =100。

解法一，Η0： ≤0（没有显著性提高），Η1：

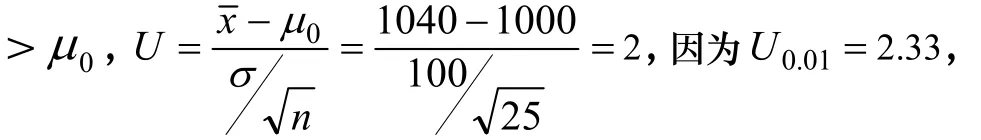
U＜ U0.01，落入接受域内，接受原假设，认为该产品使用寿命没有显著性提高。

解法二，Η0： ≥0（有显著性提高），Η1： ＜

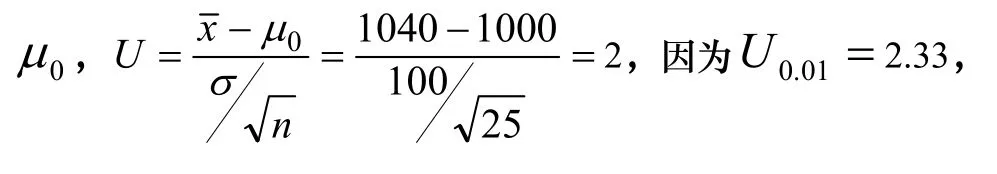
U＞- 01.0U =-2.33 ，落入接受域内，接受原假设，与解法一得出的结论相反，认为该产品使用寿命有显著性提高。

对这个问题我们都是接受原假设，但是结论相反，因此，其中必有一种方法犯了第二类错误，即“取伪”错误，这类问题如何解决呢？奈曼与皮尔逊（Neyman＆Pearson）提出一个原则，即在控制犯第一类错误的概率 的条件下，尽量使犯第二类错误的概率 小。这其中蕴含了这样一种思想：我们只对犯第一类错误的概率 加以限制，而不考虑犯第二类错误的概率[6]。根据两类错误此消彼长的关系，既然发生了“取伪”错误，不妨增加 值，在上述例题中若取 =0.05，对应解法一有:U = 2 >U0.05=1.65,拒绝原假设，认为该产品使用寿命有显著性提高；对应解法二有：U= 2 >−U0.05=−1.65，接受原假设，也认为该产品使用寿命有显著性提高。在 =0.05的水平上，两种方法得出了一致性结论，根据上文的论述，解法一更有说服力。

可见在检验中， 的概率是可以人为控制的，通过控制 而改变 ， 的含义是当原假设正确时却被拒绝的概率或风险， 通常取值0.05或0.01，但在使用时究竟取多大，应视具体情况和根据专业知识判断。“一般来说，哪一类错误所带来的后果越严重、危害越大就把哪一类错误作为首要的控制目标。[7]”需 要衡量两类错误所付出代价的大小, 如果“取伪”代价大, 则取较大 。如“弃真”代价大, 则取较小 , 容忍较大 。

[1]权德庆等.体育统计学科现状与发展趋势[J].西安体育学院学报,2008.

[2]费宇.应用数理统计[M].北京:科学出版社,2007.

[3]丛湖平.体育统计学[M].北京:高等教育出版社,2007.

[4]贾俊平等.统计学(第二版)[M].北京:中国人民大学出版社,2004.

[5]祁国鹰等.体育统计简明教程[M].北京:北京体育大学出版社,2004.

[6]康铁祥.深入理解假设检验原理[J].统计教育,2001,(1).

[7]贾俊平等.统计学(第二版)[M].北京:中国人民大学出版社,2004.

G80-32

A

1673-2219（2011）12-0193-03

2011-01-06

曹远红（1977—），男，湖南长沙人，湖南师范大学体育学院体育人文教研室体育统计学教师，体育人文博士，研究方向为体育统计的原理和应用、体育人文。

（责任编校：张京华、何俊华）