基于粒子群优化算法的树状注水管网拓朴优化
2011-11-21向华
向 华
(长江大学计算机科学学院,湖北 荆州 434023)
罗 颖
(湖南大学信息科学与工程学院,湖南 长沙 410082)
基于粒子群优化算法的树状注水管网拓朴优化
向 华
(长江大学计算机科学学院,湖北 荆州 434023)
罗 颖
(湖南大学信息科学与工程学院,湖南 长沙 410082)
树状注水管网拓扑优化设计问题是一个涉及离散变量、连续变量的大型非线性优化问题。使用粒子群优化算法在现有管网的基础上进行管网优化设计。该算法是从随机解出发,根据迭代寻找最优解,通过适应度来评价解的品质。实际算例表明,该算法对树状注水管网优化效果比较明显。
粒子群优化算法;注水管网;拓扑优化
油田注水系统管网是由许多注水站、配水间、注水井及连接它们的管线组成的复杂多级网络系统,一般包括环状和树状(也称星式)2种形式。笔者拟针对树状注水管网中配水间到注水井之间的树状形式管网进行拓扑优化。注水管网拓扑优化设计问题是一个涉及离散变量、连续变量的大型非线性优化问题,该问题是布局-分配问题的扩充,已被证明为非确定多项式(NP)问题。Kennedy J[1]与Eberhart R C[2]分别从鸟群觅食过程中表现的行为得到启发而研究出粒子群优化算法 (Particle Swarm Optimization,PSO),该算法可以最大限度地用于搜索该类NP问题的最优解。笔者根据油田注水系统管网的特点建立相应的粒子群优化模型,以求解最优化的树状注水管网拓朴结构。
1 粒子群优化算法
在粒子群优化算法中,问题域在D维空间中,每个个体都是一个没有体积的粒子(点),该粒子以一定速度飞行,其飞行速度可根据自身飞行经验和同伴(领域)飞行经验进行调整。
假设第i个粒子表示为Xi=(xi1,xi2,xi3,…,xiD),第i个粒子的第d维(1≤d≤D)在第j次迭代过程中速度根据下式变化:
Vid(j)=wVid(j-1)+c1r1(pid-xid(j-1))+c2r2(pgd-xid(j-1))
(1)
式中,wVid(j-1)为惯性部分,w为惯性权重;Vid为第i个粒子第d维的速度分量;c1r1(pid-xid(j-1))为认知项[3],c2r2(pgd-xid(j-1))为社会项[4],c1、c2分别为加速常数;r1、r2分别为区间(0,1)中的随机值;pid为第i个粒子所经过的最好位置第d维位置分量;xid为第i个粒子第d维当前位置分量;pgd为粒子群群体中所有经历过的最好位置第d维位置分量。
根据式(1)求得第j次迭代第i个粒子的最新速度Vi后,其最新位置根据下式更新:
xid(j)=Vid(j)+xid(j-1)
(2)
式中,xid(j)为第i个粒子在第j次迭代后的第d维值。
式(1)的惯性部分反映的是粒子的维持先前速度的趋势,最初将w固定取值为1.0[1-2],但这种做法很难使算法快速收敛,后来Bandura A[4]将w由0.9逐步降为0.4,而Shi等[5]采用随机近似理论分析PSO的动态行为,提出了将w随更新代数递减至0的方法。上述方法使得w随着迭代次数的增加逐步变小,从而使该算法在早期有较高的搜索解空间的能力,在后期可以快速收敛。
式(1)的认知项反映了粒子在飞行过程中对“经历”过的最好位置的记忆,而式(1)的社会项反映了粒子与粒子之间的知识共享群体最优记忆,也代表粒子向最优位置逼迫的趋势。最初将c1和c2固定
取值为2.0,但Ratnaweera等[6]提出c1随着迭代次数的增加,其值可以从2.5线性地减至0.5,以使单个粒子逐步向最优位置靠近,而c2随着迭代次数从0.5线性地增至2.5,以使群体逐步逼近最优。
2 管网拓朴优化数学模型
以注水井与配水间的隶属关系及配水间的位置作为优化设计变量,以注水系统管网管线长度最小为目标函数,则树状注水系统管网拓扑优化的数学模型为[7-8]:
(3)
式中,f为管线长度;Nw为注水井数量;Np为配水间数量;δij表示第i口井与第j个配水间的连接关系,其值为1或0,0表示没有连接,1表示有连接;xi、yi为第i口井位置坐标;Dxj、Dyj为第j个配水间的坐标位置。
由式(3)可以看出,要使各注水井到配水间总的管线长度最短,必须满足下列条件[9]:
Nw∈[Dwmin,Dwmax]
(4)
式中,Dwmin、Dwmax分别为每个配水间连接各注水井的最小值和最大值。
所以,树状注水管网拓朴优化设计的实质就是寻找最佳连接方案的过程。
3 算法求解
3.1编码
编码前,首先对所有的注水井与配水间编号,分别从编号1开始逐渐增加,使注水井与配水间分别都有一个唯一且连接的序列号,设最大配水间编号为dp max,最大注水井编号为dz max。然后,再把粒子群的维度设为dp max,并令第i个粒子Xi=(xi1,xi2,xi3,…,xdp max)中的xij表示第j(1≤j≤dp max)个配水间,连接的是第xij(1≤xij≤dz max)号井。
3.2产生初始粒子
对每一维xij的产生,都可以采用随机数在[1,dz max]中选取,对最后的Xi只需要判断基本可行性,即所产生的Xi中的连接到相同配水间的数量Nw∈[Dwmin,Dwmax]即可,如不满足,可以采用随机调整修正或丢弃重新产生[8]。
3.3确定适应函数
管网整体优化的过程是使目标函数值最小,属最小化优化,应加以调整,可采用归一化方法:
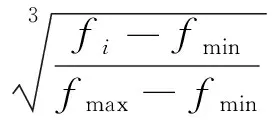
(5)
式中,Fi为适应值;fmin为历史最小目标函数值;fmax为历史最大目标函数值;fi为第i个粒子的目标函数值。
变换后,最大适应值与最小目标函数值相对应,最小适应值与最大目标函数相对应,并且在fi较小时,适应值fi差距较大,这样有利于选择优势粒子。
3.4算法步骤
使用粒子群优化算法进行树状注水管网拓朴优化的算法步骤如下:①随机产生一定符合要求的粒子群,并计算各粒子的适应值;②计算各粒子适应值,并依据式(1)与式(2)重新计算粒子群的新位置;③ 检测新的粒子是否满足配水间数量的限制,如不满足,做随机调整或丢弃后重新生成新的粒子补充;④如果已经达到大最迭代次数,输出最大适应值所对应粒子,即为解,算法结束,否则转向步骤②。
4 应用实例
以某油田采油厂注水区块为例,该区块共有注水井41个,配水间12个(见图1)。根据粒子群优化算法,使用VC++工具编写注水系统的软件,得到优化后的注水管网(见图2)。原有注水管网管线总长为30.07km,使用粒子群优化算法后,管线总长减少为28.01km,降低幅度为6.85%,可见采用该优化方案的效果十分显著。
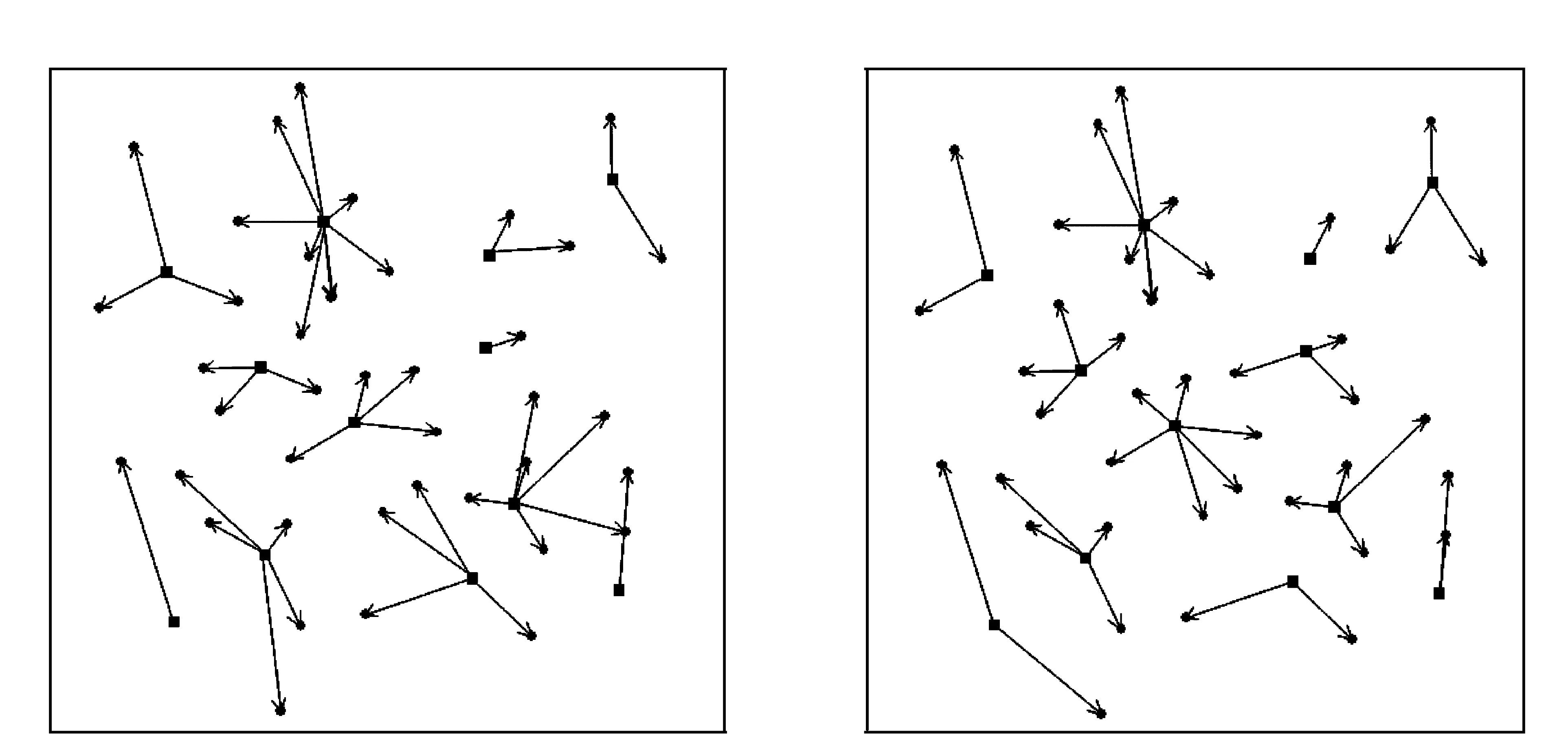
图1 使用粒子群算法优化前的注水管网 图2 使用粒子群算法优化后的注水管网
5 结 语
把注水井与配水间的匹配位置关系做为粒子优化变量,以最短管网线为目标函数,同时结合配水间的上下限约束条件建立了树状管网粒子群拓朴优化数学模型。根据目标函数特点,对目标函数做了适当变换,以最大适应值为目标进行求解,最后使用VC++为工具,对实际的油田注水管网进行优化求解,并与现在管网进行比较。结果表明,使用粒子群优化算法可以有效优化现有注水管网拓朴结构,节省管网建设投资。
[1]Kennedy J,Eberhart R C. Particle swarm optimization[A].Proc IEEE Int Conf on Neural Networks[C].Perth, 1995:1942-1948.
[2]Eberhart R C, Kennedy J A. A new optimizer using particle swarm theory[A]. Proc The Sixth Int Symposium on Micro Machine and Human Science[C].Nagoya, 1995:39-43.
[3]Thorndike E L. Animal I ntellig ence: Emp ir ica l Stud ies[M] . New York: MacMillan, 1991.
[4] Bandura A. Social Founda tions of Thought and Action: A Social Cognitive Theory [M]. New Jersey: Prentice-Hall,1986.
[5]Shi Y,Eberhart R C, Empirical study of particle swarm optimization [A]. In Proc IEEE Congr Evol Comput[C]. Washington, 1998:1945-1950.
[6]Ratnaweera A, Halgamuge S K,Watson H C. Self-Organizing Hierarchical Particle Swarm Optimizer with Time-Varying Acceleration Coefficients [J]. IEEE Transactions on Evolutionary Computation, 2004,8(3):240-255.
[7] 刘杨.油田注水系统智能优化方法研究[D].大庆:大庆石油学院,2006.
[8] 康正凌,袁宗明.树枝状天然气管网优化设计[J].天然气工业,2001,21(3):76-78.
[9]刘扬.石油工程优化设计理论及方法[M].北京:石油工业出版社,1994.
[编辑] 李启栋
10.3969/j.issn.1673-1409.2011.09.024
TP301.6
A
1673-1409(2011)09-0076-03
