线性复合油气藏试井解释模型及典型曲线分析

2011-11-20罗建新张烈辉

长江大学学报(自科版) 2011年4期

关键词：试井油气藏均质

罗建新，张烈辉

赵玉龙，刘启国

(油气藏地质及开发工程国家重点实验室(西南石油大学)，四川成都 610500)

线性复合油气藏试井解释模型及典型曲线分析

罗建新，张烈辉

赵玉龙，刘启国

(油气藏地质及开发工程国家重点实验室(西南石油大学)，四川成都 610500)

对于河道沉积环境所形成的条带状油气藏，储层物性的平面分布往往表现出较强的不连续性，呈现出线性组合的特征。在对这类油气藏的压力恢复和压力降落测试数据进行试井解释时，需要考虑其特殊性。根据表皮效应和井筒储集效应，通过建立外边界封闭线性复合油气藏试井解释模型，并结合拉普拉斯变换、有限傅里叶余弦变换以及正交变换法对该模型进行求解。利用Stehfest数值反演算法以及计算机编程技术编制了计算程序，绘制了线性复合油气藏的井底无因次压力典型曲线，并对各个流动阶段以及各种参数对曲线形态的影响进行了分析。该研究丰富了现代试井解释模型，对该类油气藏试井资料的解释具有指导作用。

线形复合油藏；渗流模型；试井解释；典型曲线

贾永禄[1，2]等人建立了均质多重不等厚地层试井分析模型，并对样板曲线进行了分析；向开理[3]、田冷[4]和何维署[5]等对径向复合油气藏进行过研究。但是针对条带状油藏的不稳定渗流模型的相关研究较少。为此，笔者建立了线性复合油气藏渗流物理模型，利用数学物理方法，对模型进行了求解，并利用计算机编程技术绘制了该类油气藏的压力典型曲线，并对各个流动阶段以及各种参数对曲线形态的影响进行了分析。

1 物理模型

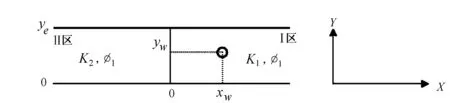
图1 复合矩形油藏示意图

复合矩形油藏示意图如图1所示，其边界均封闭，油藏被分为左右2部分(Ⅰ区和Ⅱ区)，其孔隙度和渗透率均不相同，Ⅰ区中任意位(xw,yw)有一口垂直井，以定产量qsc进行生产。其余假设条件为：①储层均质水平等厚，且每一区都各向同性。②流体在储层中的渗流满足达西渗流公式，忽略重力和毛管力的影响。

2 数学模型

根据上述假设和图1中所建立的坐标系，以渗流力学理论为基础，得到考虑地层参数变化的2区线性复合条带状油气藏的无因次化渗流模型。

Ⅰ区的渗流方程为:

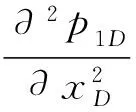
(1)

10-3μm2；h1为Ⅰ区油层厚度，m；pi为原始油层压力，MPa；p1为Ⅰ区压力，MPa；B为体积系数；q为井产量，m3/d；μ1为Ⅰ区流体粘度，mPa·s；φ为孔隙度；Ct为总压缩系数，MPa-1；t为时间，s；xeD1为Ⅰ区无因次长度；x为横坐标，m；y为纵坐标，m；rw为井半径，m。

Ⅱ区的渗流方程为：

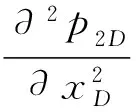
(2)

式中，p2D=2πk1h1(pi-p2)/Bqμ1，η=[(φμCt)1k2]/[(φμCt)2k1];p2为Ⅱ区压力，MPa；xeD2为Ⅱ区无因次长度；k2为Ⅱ区渗透率，10-3μm2。

初始条件：

p1D(xD,yD,0)=0p2D(xD,0)=0

(3)

边界条件：

(4)

衔接面条件：

(5)

式中，H=h2/h1，M=μ1k2/μ2k1。

3 模型的求解

对该模型引入关于时间tD的Laplace变换[6]，同时引入关于yD的有限余弦Fourier变换[7]。则Ⅰ区的渗流方程变为:

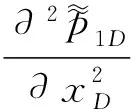
(6)

式中，z为拉氏变量；βm=mπ/yeD；m为有限Fourier余弦变换变量。

Ⅱ区的渗流方程为:

(7)

求解式(7)可得：

(8)

对式(6)引入关于xD的正交变换[6]:

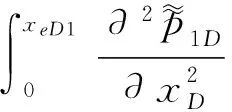
(9)

结合衔接面条件，解之可得：

(10)

4 典型曲线的绘制

取xD=xwD,yD=ywD代入式(10)中，得到井筒的无因次压力解。由Duhamel原理[11]并考虑表皮系数S和井储效应CD，可以得出井筒压力表达式：

(11)

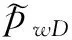
利用Stefest数值反演[9]方法以及计算机编程技术可以得到真实空间下的不稳定井底无因次压力分布典型曲线，如图2所示。

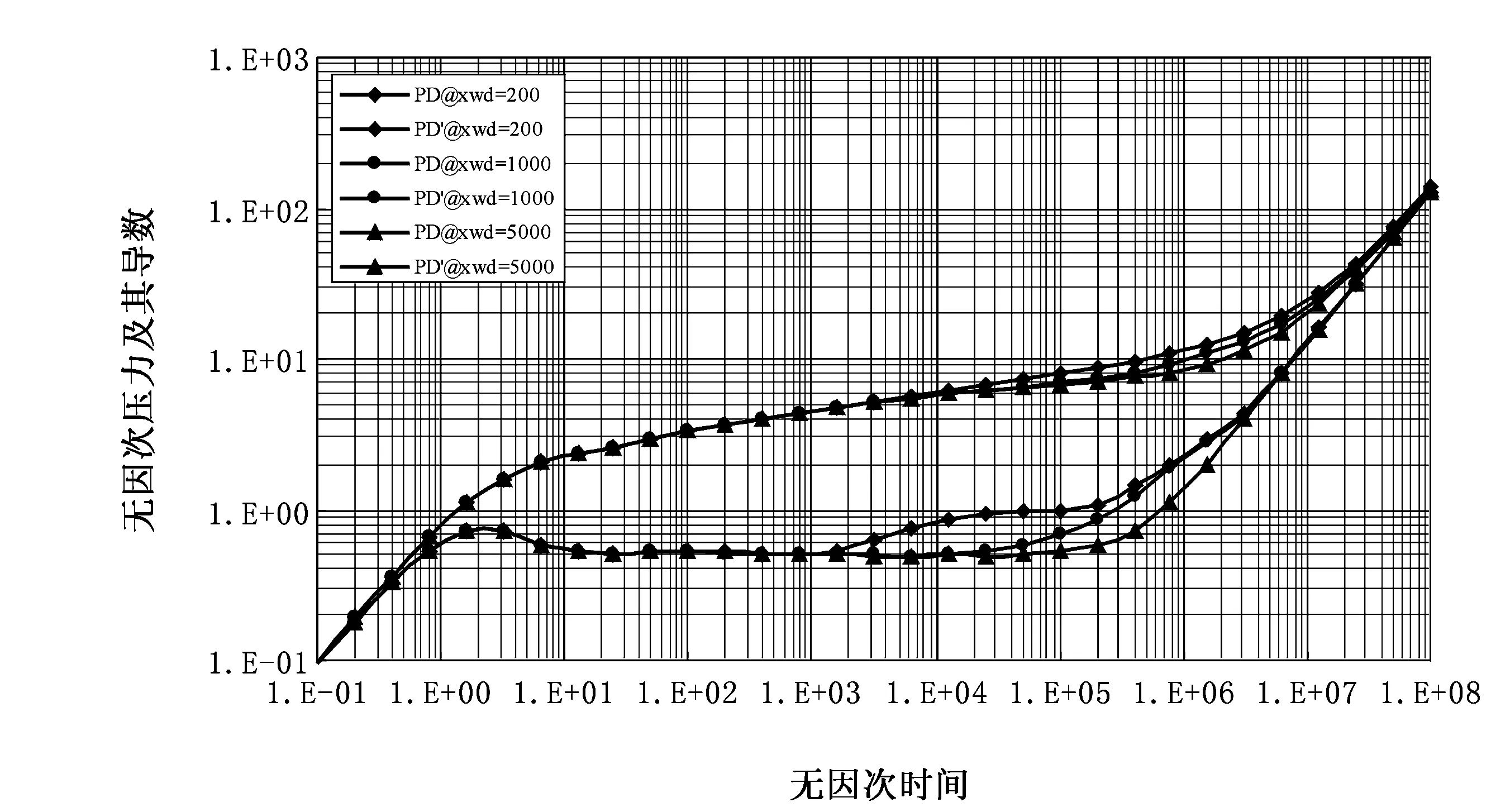
图2 不稳定井底无因次压力及其导数曲线典型图版

由图2可以看出，这类油藏的压力动态特征表现为以下阶段：①井筒储集阶段。在该阶段无因次井底压力及其导数曲线表现为一条斜率为1的直线。②Ⅰ区径向流阶段。在该阶段无因次压力导数曲线表现为一条无因次压力导数值为0.5的水平线，持续时间主要受井与Ⅰ、Ⅱ区分界线的距离影响，距离越大，持续时间越长。③压力波传递到Ⅱ区后的阶段。在该阶段无因次压力导数曲线出现第2条水平线，无因次压力导数值的大小受Ⅰ、Ⅱ区物性差异的影响，差异越小，越接近0.5；该阶段持续时间的长短主要受井与y方向边界距离的影响，距离越大，持续时间越长。④拟稳定流阶段。在该阶段压力导数曲线表现为一条斜率为1的直线。