参数未知机器人含时变函数的自适应控制算法研究

林 婷

(福建农林大学机电工程学院，福建 福州 350002)

李明月

(福建戴姆勒汽车工业有限公司，福建 福州 350119)

参数未知机器人含时变函数的自适应控制算法研究

林 婷

(福建农林大学机电工程学院，福建 福州 350002)

李明月

(福建戴姆勒汽车工业有限公司，福建 福州 350119)

对参数未知机器人系统含时变函数的自适应控制算法进行了研究。针对控制系统自适应律中参数难以确定的问题，推导设计了一含时变函数的新的参数自适应律，该时变函数包含了系统惯性参数及系统动力学特性。在二杆平面机器人系统上进行数值仿真分析，仿真结果证实了所设计控制器的有效性。

机器人；参数未知；自适应控制；时变函数

对于具有参数未知或参数不确定机器人系统的轨迹跟踪控制问题一直是控制界及机械行业的研究热点[1]，在系统参数线性化情况下，由于自适应控制[2-3]具有可在线估计系统未知参数并进行调整的巨大优点而得到研究人员的广泛关注。但使用自适应控制对机器人轨迹进行跟踪时，必须对控制器中自适应律中的参数进行一个初始值的确定，该初始值一般为固定值，且要进行大量的试验调整才能得出一个较好的结果。为了更好地解决该参数的选取问题，笔者对参数未知的机器人系统进行了自适应控制研究，对于自适应律中的参数选取进行改进，使用了一个含时变函数的参数自适应律，由此解决了自适应律中参数如何确定的难点。 该时变函数为一包含系统惯性参数及系统动力学特性的函数，使用该时变函数使整个自适应控制方案更加稳定可靠。

1 自适应控制中的参数估计

不考虑摩擦和其他干扰的情况下，一个n杆的机械臂动力学方程可写为：

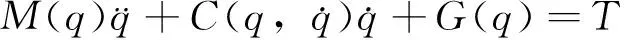
(1)

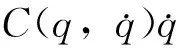
(2)

针对该机器人系统可设计如下控制方案：

(3)

式中，K为正定矩阵；σ为待定的与跟踪相关的量。

其他参数如下式所示：

(4)

如果σ取为：

(5)

则式(3)中的Kσ项等同于一个针对跟踪误差的PD控制器。

如果该控制器的计算模型在结构上与机器人的动力学模型相同，只是其中的参数存在未知的情况，则控制律(3)可修改为：

(6)

将式(6)代入式(2)有：

(7)

其他系统建模误差可表示为：

(8)

定义如下Lyapunov函数：

(9)

式中，B和Kθ为正定对角矩阵。

选取B=2ΛK并利用系统的斜对称性：

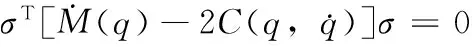
将V对时间求导可得：

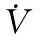
(10)

通过选择如下参数自适应律:

(11)

(12)

则系统为全局渐近收敛。

2 含时变函数的参数自适应律

利用式(11)的参数自适应律时，必须对式中的Kθ进行选取。Kθ选取的准确与否，对系统控制精度将产生一定影响。针对上述情况，为该机器人控制系统设计了新的含时变函数的自适应律。

为了获得新的参数自适应律，选取如下Lyapunov函数：

(13)

式中，Ω为正定的时变函数矩阵。

式(13)对时间求导可得：

(14)

同样，选取B=2ΛK并利用系统的斜对称性，则：

(15)

因为K>0、Λ>0，式(15)的前2项将小于等于零，即：

(16)

为了保证系统的稳定性，则式(15)的第3式必须满足：

(17)

由于式(17)中Ω的选取并没有一个固定的解，可选取：

(18)

式中，I为单位矩阵。

将式(18)代入式(17)，有：

(19)

(20)

(21)

整理式(21)可得：

(22)

对式(22)进行积分，则：

(23)

(24)

(25)

同样，式(25)可使式(15)满足：

则系统同样满足全局渐近收敛。

3 仿真算例

图1 二杆机器人系统

以作平面运动的二杆机器人系统(见图1)为例验证所设计控制算法的可靠性。系统惯性参数为：m1=10kg；m2=5kg；l1=1m；l2=1m；杆1的极惯性矩I1=10/12kg·m2；杆2的极惯性矩I2=5/12kg·m2。

利用式(6)、式(11)和式(24)给出的自适应控制方案进行系统控制仿真运算，图2和图3分别为关节1和2的轨迹跟踪情况，图4为采用常规自适应控制对机器人进行控制时的跟踪误差，图5为采用笔者所设计的含时变函数的自适应控制对机器人进行控制时的跟踪误差。

图2 关节1轨迹跟踪情况 图3 关节2轨迹跟踪情况

图4 一般自适应跟踪误差 图5 时变自适应跟踪误差

由图2和图3可知，所设计控制方案可使机械臂的关节1及关节2很好地跟踪其期望运动。当使用常规自适应算法对机器人进行控制时，图4最终的跟踪误差达到0.05rad；而使用笔者所设计的含时变函数的自适应律对机器人进行控制时，图5所示的最终跟踪误差仅有0.02rad。因此，含时变函数的自适应律可以更好地解决自适应参数的选取问题，从而达到更好的跟踪精度。

[1]Bondi P, Casalino G, Gambardella L. On the iterative learning control theory for robotic manipulators[J]. IEEE Journal of Robotics and Automation, 1988(4): 14-22.

[2] Slotine J J, Li W. On the adaptive control of robotic manipulator [J].Int J Rob Res，1987, 6(3): 49-59.

[3] Sun F C, Sun Z Q, Feng G. An adaptive fuzzy controller based on sliding mode for robot manipulators[J]. IEEE Trans on Systems,1999, 29(4): 661-667.

[编辑] 李启栋

10.3969/j.issn.1673-1409.2011.11.025

TP273.2

A

1673-1409(2011)11-0076-04