铜绿山矿I2号矿体开采的突水风险评价

戴宏辉，陈小康，郑瑞朋，汪茂华，史秀志

(1.大冶有色金属公司铜绿山铜铁矿，湖北大冶市435101;2.中南大学资源与安全工程学院，湖南长沙410083)

铜绿山矿I2号矿体开采的突水风险评价

戴宏辉1，陈小康2，郑瑞朋1，汪茂华1，史秀志2

(1.大冶有色金属公司铜绿山铜铁矿，湖北大冶市435101;2.中南大学资源与安全工程学院，湖南长沙410083)

根据铜绿山矿I2号矿体的开采条件，综合应用模糊数学方法和层次分析法(AHP)评价该矿体开采的突水风险。首先建立采场突水的风险评估指标体系，并用层次分析法客观地确定各因素的权重，再根据模糊数学理论建立模糊综合评判，从而确定该采场突水风险级别。结果表明，把层次分析法与模糊评判方法综合应用于采场突水的风险评估具有一定的科学性和合理性。

采场突水;模糊数学;层次分析法(AHP);风险评价;铜绿山矿

回采铜绿山矿I2号矿体下部残矿时，采准巷道所穿过的岩层物理力学性质较差，含水率高，整体强度低，且采准巷道须穿过I2号矿体成矿断层，断层较宽，充填物不明，可能含水含泥。断层出露于南坑底部，可能成为南坑水体与井下涌水的联系通道。同时，矿山长期受民采影响，在巷道掘进或采场矿石回采过程中，随时可能贯穿民采空区。若空区含水含泥，则掌子面可能迅速被淹没，甚至出现淹井。此外，相关资料显示，I2号矿体下盘为大理岩，围岩中可能存在溶洞。所以，为保证掘进及采矿过程安全，须对采场突水风险进行评估，并提出相应的安全控制技术措施［1］。

1 采场突水风险评估指标体系

突水事故的发生是诸多因素综合影响的结果，不同因素之间相互关联、相互影响，各因素的所占权重和作用也各不相同，且有些因素不能作定量分析，与此同时，这些因素的变化与发生突水灾害之间不存在明确的数学函数关系，不可能建立确定性数学模型［1］。如何综合分析这些因素所起的作用，符合实际地进行突水事故风险评估是多年来人们一直关心的问题。系统工程［2］常用的层次分析法(AHP)［3～6］为这种复杂系统提供了简便实用的决策方法，它所提供的思路恰好适合于分析和解决这类问题。把层次分析法的量化结果与模糊数学中的综合评判方法［7］结合起来，既能克服因专家个人见解的偏差而产生的随意性，又可避免单纯模型数学方法中的模糊不确定性带来的误差。因而，把层次分析法与模糊评判方法综合应用于采场突水的风险评估，可得出切合实际的评判结果。

用AHP评价采场突水风险，首先确定评价目标采场突水风险，然后根据评估指标选取的原则并参考以往研究成果，选择地质条件、水文条件和开采条件等3个因素作为评估体系的准则层。在准则层下又细化成11个不同的评估指标构成指标层，并建立一个完整的采场突水风险评估指标体系，见表1［1］。

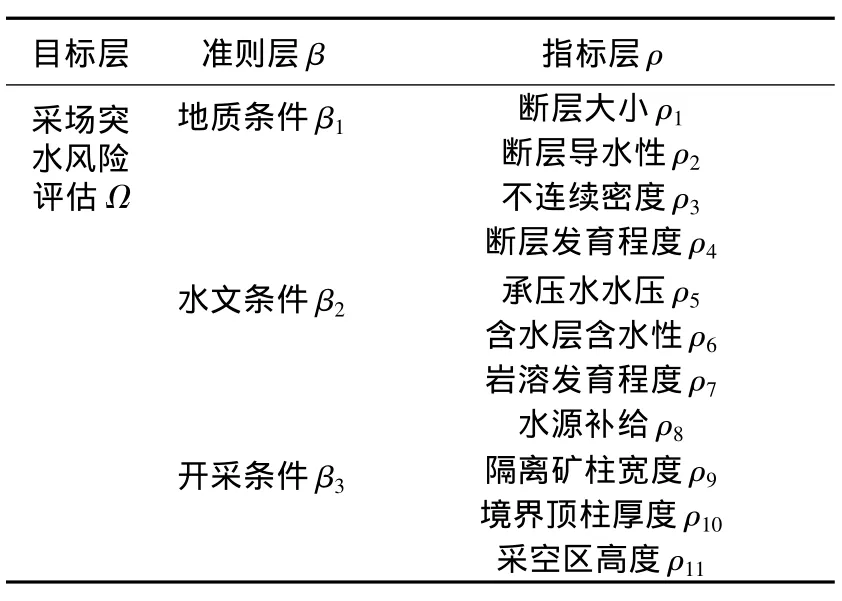
表1 采场突水风险评估指标体系

2 层次分析法确定各评价指标权重

鉴于采场突水风险评估指标体系中各因素的权重分配对评估结果的影响很大，本文提出一种层次权重决策分析方法，通过逐层比较各种关联因素的重要度来为分析、决策提供定量的依据。为保证排序结果的可靠性，必须进行一致性检验。AHP基本计算步骤如下［3～6］。

(1)构造比例尺度。采用Satty的9标度法［2～5］构造成对比较阵，将复杂的定性问题量化处理，对指标的重要程度进行标度划分。

(2)判断矩阵的确立。按照层次结构模型，构造判断矩阵。根据各因素的重要性比较矩阵并进行计算，所得判断矩阵相应计算结果用表列出。对于采场突水风险评估(Ω)而言［1］，根据层次分析法的9标度法，判断矩阵Ω－β为相对于目标层Ω准则而言，各准则层β1～β3间的相对重要性(见表2)。判断矩阵β1－ρ为相对于地质条件(β1)准则而言，各指标层ρ1～ρ4间的相对重要性(见表3)。同理可得判断矩阵β2－ρ，β3－ρ，如表4～5所示。

表2 判断矩阵Ω－β

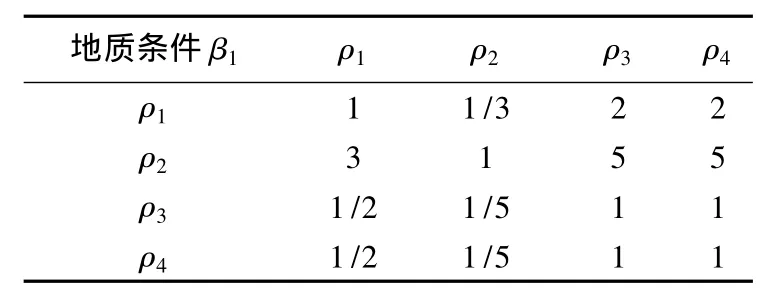
表3 判断矩阵β1－ρ

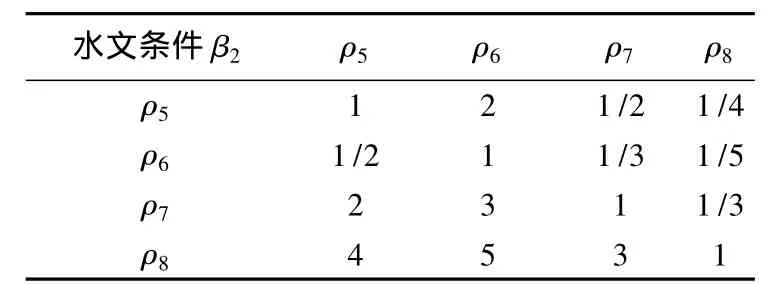
表4 判断矩阵β2－ρ

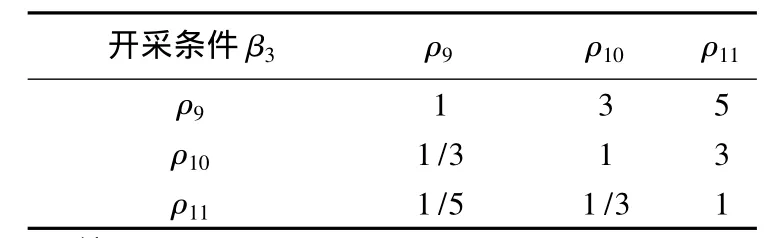
表5 判断矩阵β3－ρ

(3)计算权重系数。用近似计算方法(和积法和方根法)计算权重系数。本文用方根法［3～6］计算权重系数。

计算判断矩阵的最大特征根ζmax:

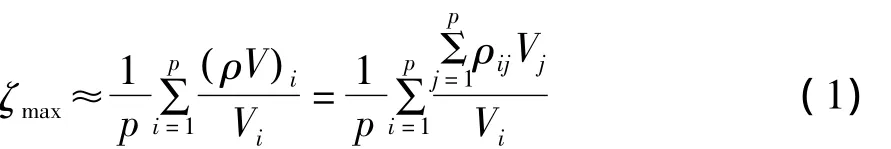
式中，ρ为判断矩阵，(ρV)i为向量ρV的第i个分量。

(4)一致性检验。为检验判断矩阵的一致性，使其判断结果更好地与实际情况相吻合，通常，将一致性比率(CR)作为一致性检验判别式，则有:

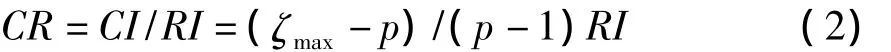
式中，CI为一致性指标，p表示判断矩阵阶数;RI为随机一致性指标均值，其取值见表6。当CR＜0.1时，可认为所得比较矩阵的判断是满意的，评价结果确实可信，否则需重新调整相应的判断矩阵。

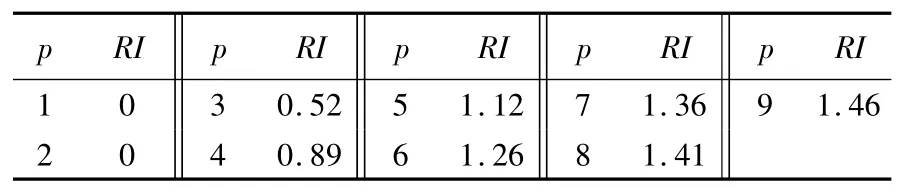
表6 平均随机一致性指标RI

经过一致性检验，表2～5的判断矩阵均满足CR＜0.1(见各判断矩阵表注释)，认为层次单排序［3～6］结果达到满意的一致性。通过层次总排序［3～6］计算出各指标的组合权重(见表7)，并对层次总排序结果用单排序指标加权求和的方法进行一·W=0.0137

致性检验。其中CI=i;RI=·W=0.845i，则CR=0.016＜0.1。由此可见，层次总排序的结果具有满意的一致性。

3 I2号矿体突水风险模糊综合评判

鉴于突水风险评价中存在诸多不确定性因素，且突水风险等级与分级标准显现出模糊性，为此引入模糊数学［4～7］，实现矿体突水风险等级评价。

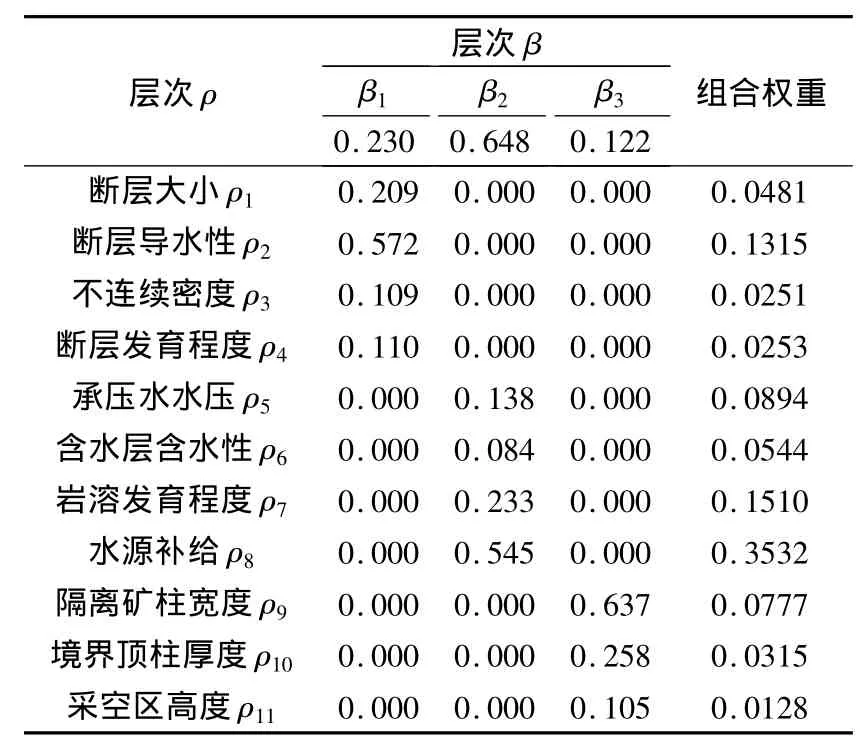
表7 层次分析结果

(1)模糊评判数学模型。假设U={u1，u2，…，um}为m种因素构成的集合，建立评价因素集;V={v1，v2，…，vs}为评判对象的s个等级所构成的集合，建立评判集;因素的权重分配可视为U上的模糊子集W，W={w1，w2，…，wm}。式中wi为因素集中ui的权值，wi≥0，且。综合后的评判也应看作为V的模糊子集，记为:B={b1，b2，…，bs}，其中bj反映了第j种决断在评判总集V中所占的地位。假定有一个U与V之间的函数关系R=(rij)s×m，则三元体(U，V，R)构成了模糊综合评判，即:

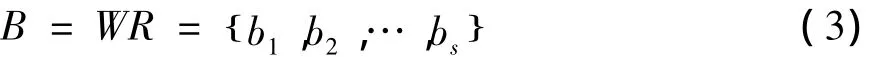
(2)评价集的建立。根据矿井突水预测与防治方面的实际数据和实践经验，依照综合评判的方式，将采场突水危险性分为5级，即V={小，较小，较大，大，很大}。不同因素的隶属度值对应于不同突水危险性评价等级的单因素评价值，见表8［1］，由此可以确定各评价指标的单因素评价矩阵。

(3)隶属矩阵的确定。根据评价因素与采场突水风险评估(Ω)之间的相关性，采用较为直观的梯形隶属函数:S型、反S型两种［4～7］。在本研究所选的指标集中，断层大小、不连续密度、承压水水压、水源补给和采空区高度与采场突水可能性呈正相关，适用于S型隶属函数曲线，隔离矿柱宽度与境界顶柱厚度与采场突水可能性呈负相关，适用于反S型曲线［1］。

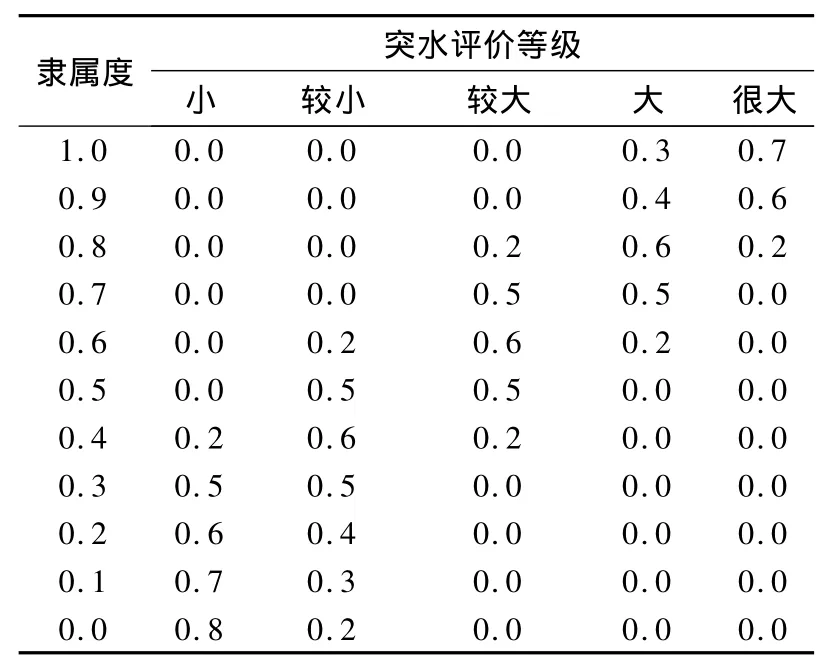
表8 单因素隶属度评价值

对于断层导水性、断层发育程度、含水层含水性和岩溶发育程度等这四个定性指标，采用阶梯型隶属函数将其对应为［0，1］上值(见图1)。

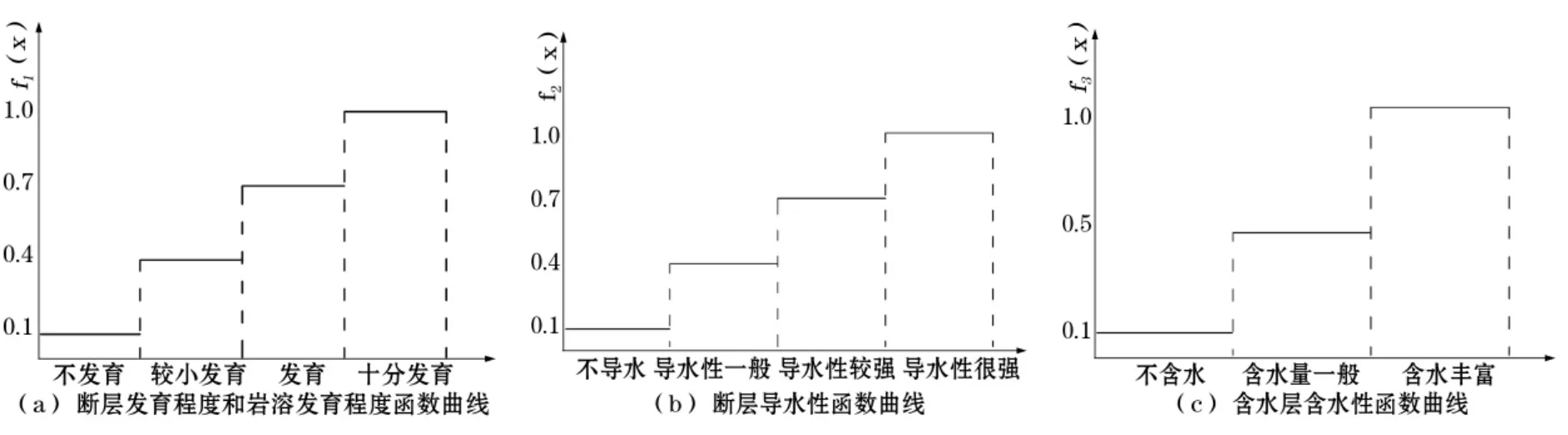
图1 部分评价指标阶梯型隶属函数

铜绿山矿I2号矿体下部残矿矿体上盘有一大断层将矿体与围岩隔开，断层最宽处宽可达7m，断层导水性较强，不连续密度6条/m，断层发育;下盘为大理岩，含水量丰富，水压1.9MPa，溶洞裂隙较发育，透水性较强，上部－187m以上已采用露天开采，南露天直接汇水面积约45.8万m2;隔离矿柱宽度为5m，境界顶柱厚度为15m，采空区高度6 m［1］。

由上述地质、水文和开采条件确定评判区域的各影响因素和评价指标，根据每个评价因素的隶属函数计算得出各自的隶属度值，从而构造出各隶属矩阵，并求得隶属矩阵R:

(4)综合评判。通过AHP可计算出各指标权重W;并结合fuzzy理论构造出最终隶属矩阵R，由式(2)可得采场突水的风险评估为:

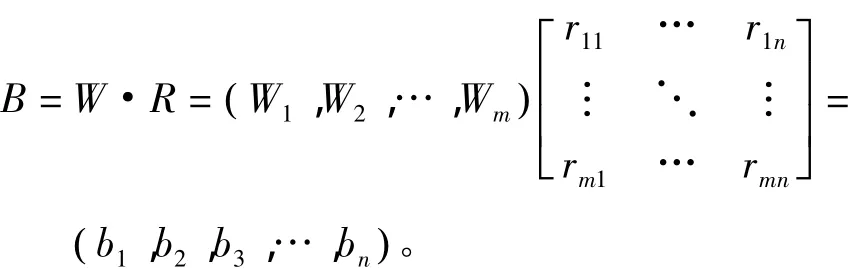
由式(3)可求得采场突水的风险评估向量B为:B=W·R=(0.0390，0.1172，0.4298，0.3759，0.0381)。

根据最大隶属度原则［4～7］，对照突水危险性评价等级的划分，评判结果中最大数值0.4298所对应的等级为“较大”，即采场突水的危险性“较大”。

4 结语

将层次分析和模糊数学应用到铜绿山I2号矿体开采过程中突水风险评价，评判结果显示采场突水的危险性“较大”。采用定性与定量分析相结合的评价法，使评价结果确实可信，此外，对矿体突水风险进行多级模糊综合评价，有助于决策者很快辨识到其薄弱环节，并提出有针对性的改进措施，进而确保掘进及采矿过程的安全。

［1］陈小康.露天坑下残矿回收安全控制技术研究［D］.长沙:中南大学，2010.

［2］黄贯虹，方刚.系统工程方法与应用［M］.广州:暨南大学出版社，2005.

［3］王莲芬，许树.层次分析法引论［M］.北京:中国人民大学出版社，1990.

［4］杨扬，冯乃琦，余珍友，等.基于层次分析和模糊数学的采空区稳定性综合评价［J］.安全科学技术，2008，60(5):37－39，42.

［5］李俊芳，吴小萍.基于AHP－FUZZY多层次评判的城市轨道交通线网规划方案综合评价［J］.武汉理工大学学报，2007，4(2):205－508.

［6］谢振华，倪成敏.基于层次分析和模糊数学的电解铝生产安全评价［J］.安全，2008，29(1):8－11.

［7］彭祖赠，孙韫玉.模糊数学(Fuzzy)及其应用［M］.武汉:武汉大学出版社，2002.

2011－03－06)

戴宏辉(1973－)，男，湖南桃江人，工程师，主要从事采矿设计与技术管理工作。