基于Bellman-Ford算法的动态最优路径算法设计

宫恩超，李鲁群

(上海师范大学信息与机电工程学院，上海200234)

基于Bellman-Ford算法的动态最优路径算法设计

宫恩超，李鲁群

(上海师范大学信息与机电工程学院，上海200234)

针对动态变化交通流下的最优路径问题，提出基于Bellman-Ford算法的动态最优路径算法。并用试验与仿真说明该算法可以迅速完成动态最优路径的计算。结果显示，在处理该路段突发的交通堵塞状况时，该算法可以节约行驶权重百分比大约在30%～60%。

动态;Bellman-Ford算法;最优路径

一、引 言

GIS对空间最优路径分析主要基于Dijkstra算法，如ArcInfo中的Network采用二叉堆优先级队列来实现Dijkstra算法，GeoStar的网络分析采用快速排序的FIFO队列来实现Dijkstra算法。随着计算机网络、数据采集系统的技术进步，人们已经可以快捷地实时获取瞬息万变的动态交通路况信息，在这种情况下，实时进行空间分析规划动态最优路径已经成为当今亟待解决的问题之一。传统静态的Dijkstra算法已无法解决交通网络中的实时导航、通勤、调度等时刻变化的交通流量情况。针对该问题，本文提出基于Bellman-Ford算法的动态最优路径算法来实现动态交通流量下的最优路径计算。

二、国内外研究现状

目前针对动态最优路径问题的研究主要集中在两方面:①从算法本身分析并改进，力求在算法时间复杂度上不断取得突破;②对交通网络结构进行相应的预处理工作，例如将交通网络分层，高层次的网络是主干道，用主干道将整个网络分成多个自然网络。在路径查询时逐步削减初始图，即网络低层次的起点或终点总是向毗邻的高层次上溯。每当找到进入毗邻高层次的最合理的出入口时，就在高层次的子网中继续搜索出入点之间的路径［1］。相关研究主要以启发式搜索算法为代表。启发式搜索算法就是一种针对实时动态改变的网络特征，从传统最优路径算法衍生的动态最优路径算法。在搜索过程中尽量利用目前已知的诸如迭代步数以及从初始状态和当前状态估价所需要的费用等信息，采用限制搜索范围、分解搜索目标等策略［2］。虽然它是一种以精度换速度的搜索方法［3］，但在动态最优路径的实现上提供了精确的解决方案，使最优路径的选择具有智能性。subgoals method［4-5］最优路径解决思路就是启发式搜索的一个典型代表，subgoals在最优路径中可被看做源点与目标节点之间的中间节点或链接，这样最优路径问题就被分解为2个或多个子问题。一个被用来寻找从源点到subgoals节点的最优路径，另一个被用来寻找从subgoals节点到目标节点的最优路径。

三、提出算法

1.Bellman-Ford算法流程

1)初始化:将除源点外的所有顶点的最优距离估计值d［v］←+∞，d［s］←0。

2)分布式迭代求解:反复对边集E中的每条边进行松弛操作，使得顶点集V中的每个顶点v的最优距离估计值逐步逼近其最优距离(运行|v|－1次)。

3)检验负权回路:判断边集E中的每一条边的两个端点是否收敛。如果存在未收敛的顶点，则算法返回false，表明问题无解;否则算法返回true，并且从源点可达的顶点v的最优距离保存在d［v］中。

2.Bellman-Ford算法的优势

1)Bellman-Ford算法可以处理交通网络中出现的负权回路问题，如将向某一方向行驶的车辆的权值设为正，与此方向相反的权值就为负，Dijkstra算法在处理此类负权回路问题时会陷入无限死循环。

2)与Dijkstra算法相比，虽然Bellman-Ford算法的复杂度较大，然而需要进行实时动态的路径规划时，Bellman-Ford算法又呈现出其他算法所不具备的优点。如迭代次数少，迭代过程灵活，可以进行异步、实时、分布式的规划，当威胁概率发生变化时，无需终止和重启算法，只需更新带权图G(V，E)的各边的权即可［6］。

3.动态最优路径算法

基于启发式搜索的思想，本文将subgoals method的思想融入到Bellman-Ford算法的搜索判断过程中，并提出了动态最优路径算法。通过考察源点与待选点之间，以及待选点与目标点之间的路况变化情况，利用下一个点到目标点之间的最优距离作为选择启发步。在所有起始点到待选点实际花费时间与待选点到目标点的评估时间之和中选择最小的一个，则对应的待选点为当前点，继续考虑下一步的起始节点，直到选到目标点为止［7］。

四、算法实现

1.实时交通流量模拟

实时变化的交通流量的模拟使用1～100的随机数，将其作为附加权重附加到路径的长度权重中，一起作为动态最优路径算法的权重选项参与最优路径计算，在交通网络中用路径上数量不同的点来体现该路段上的实时交通路径，点越多表示交通流量越大。在实际应用中可以将路径上的车的数量、道路平整度、宽度等影响因子作为考察对象并作为附加权重，车数量的统计可以使用GPS对每一辆车进行定位，这样就可以方便、实时地统计出路径上车的数量信息。

2.使用的关键函数及数据结构

(1)Bellman-Ford函数

int［］bellmanFord(Vector＜Edge＞edges，int nnodes，int source，int dest)

其中的参数代表的意义分别是边、节点数量、最优路径的源点、目标点。返回的是最优路径经过的路径数组，用来在地图窗口中描绘出最优路径。

(2)路径数据存储结构

Edge(int source，int dest，double weight)3个参数值分别代表边的起点、终点、权重。通过有向图的方式将交通路径数据存储起来。

3.动态最优路径选择解决思路

在车辆行驶到达新的路径后根据启发算法的one-step-look-ahead策略［8］，将新路径的起点作为动态最优路径算法的源点参数，与此同时对交通网络的附加权重重新模拟实现实时变化的交通流量，这样由动态最优路径算法得到了不断更新的最优路径，从而实现了最优路径的实时动态选择。

五、实际应用及试验结果对比分析

1.实际应用

京藏高速公路堵车现象频繁发生，长时间的交通堵塞不仅对当地的出行造成了严重的影响，而且对当地的旅游业、邮政等也造成诸多影响。这一路段堵车现象频发的主要原因有两方面:一是由于这一路段的车流量大、关卡较多容易引起车辆堵塞;二是车流量的调度出现了问题。在出现了交通拥堵情况时，由于司机不知道前方的交通已经出现了问题，交管部门又未能及时地发出警告信息，导致车辆源源不断地驶向拥堵路段。针对车流量的合理调度问题，本文提出的动态最优路径选择算法提供了有效的解决方法，在面对突发的交通堵塞情况时能及时对车流进行分流，在节约司机行驶时间、提升行驶效率、合理利用交通道路等方面表现突出。

2.试验结果对比分析

(1)各路径权重与实时交通流量的模拟

具体模拟如表1所示。

表1 各路径权重与实时交通流量的模拟

(2)程序运行过程及结果说明

1)程序运行的过程是判断从node1到node13之间的最优路径(如图1所示)。

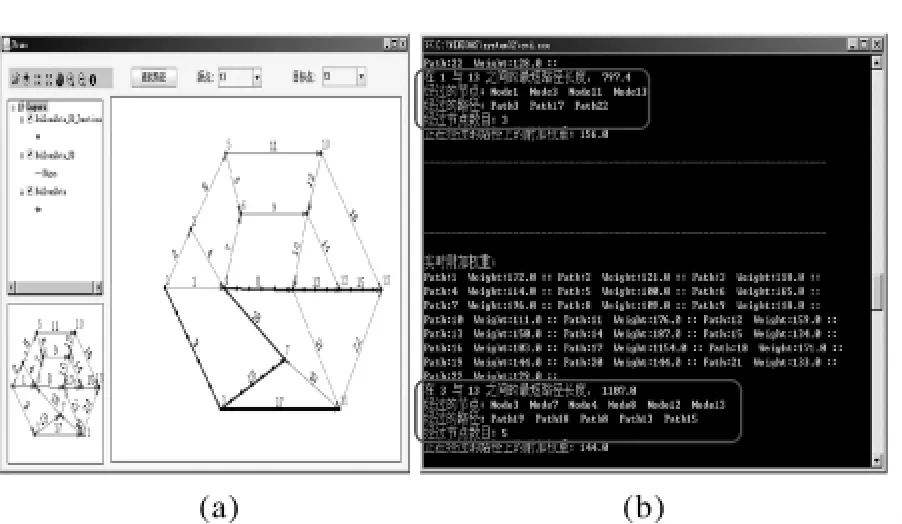
图1 程序运行过程

2)图1(a)中灰线表示车辆行驶的最优路径，黑线表示模拟的拥堵路径。灰线上的不同数量的节点意义是模拟行驶路径上的实时交通流量情况，越多表示交通流量越大。

3)从图1(a)上可以看出车辆行驶到Node3时，遇到了交通堵塞(图1(a)上用黑线标明的路段)，于是程序进行了路径的重新动态选择，车辆选择了避让。从命令窗口程序(如图1(b)所示)具体执行情况可以看出，车辆在行驶到Node3时由于路径path17的拥堵，进行了实时的动态路径选择，将行驶路径由原来的path17→path2变成了path19→path18→path8→path13→path15。

4)动态最优路径选择过程如表2所示。

表2 动态最优路径选择过程

3.当遇到交通堵塞时，静态与动态路径选择结果的对比分析

1)前提条件为当遇到交通堵塞时，堵塞路径上的实时权重模拟赋值为1 000+(100～200)之间的随机数，未被堵塞的路径上的实时权重模拟赋值为100～200之间的随机数。

2)若按照原来的路径(path17→path22)行驶，即没有实行路径的动态选择过程则总权重为weight1=pw17+pw22+apw17+apw22=158.6 +102.1+1154.0+129.0=1 543.7。

3)实际进行了路径动态选择的最优路径的总权重为weight2=1 107。

4)实施了动态最优路径算法节约的权重为weight1-weight2=436.7。

5)节约权重大约百分比为(weight1-weight2)/ weitht1=28.28%。

6)多次路径动态运行结果及对比分析如表3所示。

表3 多次路径动态运行结果对比分析

六、结束语

本文提出的动态最优路径算法，可以迅速计算出在发生交通堵塞情况时的动态最优径。从多次的试验结果可以看出，由于路径长度的不同动态最优路径算法较传统静态最优路径算法节约权重大约在30%～60%之间，由此可以说明该算法在针对突发的交通堵塞情况下可以给出一个更加快速的最优路径解决方案。

［1］ 翁敏，毋河海，杜清运，等.基于道路网络知识的启发式层次路径寻找算法［J］.武汉大学学报:信息科学版，2006，31(4):360-363.

［2］ FUA L，SUNB D，RILETTC L R.Heuristic Shortest Path Algorithms for Transportation Applications:State of The Art［J］.Computers＆ Operations Research，2006，33(11):3324-3343.

［3］ 任刚，王炜，李岩.交通建模中的最优路径算法研究综述［C］∥第一届中国交通地理信息系统(GIS-T)技术研讨会论文集.武汉:武汉大学交通研究中心，2007: 1-8.

［4］ BANDER J L，WHITE C C III.A New Route Optimization Algorithm for Rapid Decision Support［C］∥Proceedings of Vehicle Navigation Information Systems Conference.Detroit:［s.n.］，1991:709-728.

［5］ DILLENBURG J F，NELSON P C.Improving Search Efficiency Using Possible Subgoals［J］.Mathematical and Computer Modelling，1995，22(4-7):397-414.

［6］ 张冲，朱凡.基于Bellman-Ford算法的无人机路径规划研究［J］.弹箭与制导学报，2007，27(5):249-251.

［7］ 章昭辉.一种基于离散变权网络的动态最短路径快速算法［J］.计算机科学，2010，37(4):238-240.

［8］ BASELAU S，HAHNE F，AMBROSI K.Operations Research Proceedings 2007［M］.Berlin:Springer，2008: 111-116.

The Optimal Path Algorithm Design Based on Bellman-Ford Algorithm

GONG Enchao，LI Luqun

0494-0911(2011)08-0026-03

P208

B

2011-01-26

宫恩超(1986—)，男，山东烟台人，硕士生，主要研究方向为分布式GIS空间分析算法及空间信息相关无线传感器网络路由算法。