基于椭球膨胀法实现独立坐标系统的建立

于亚杰，赵英志，张月华

(河北省第二测绘院，河北石家庄050031)

基于椭球膨胀法实现独立坐标系统的建立

于亚杰，赵英志，张月华

(河北省第二测绘院，河北石家庄050031)

针对平面控制测量投影变形的两个主要因素以及它们之间的关系，阐述建立独立坐标系的方法，介绍投影面变换方法中的椭球膨胀法。同时结合实际工程项目，介绍通过TGO软件利用上述方法建立地方独立坐标系的操作步骤。

独立坐标系;坐标系统管理器;椭球膨胀法;当地点设置;投影面变换;TGO

一、引 言

在工程测量和城市测量中，由于作业区域可能位于投影带的边缘，并且测区平均高程还可能与国家大地基准的参考椭球面有较大差距，为了控制长度变形≤2.5 cm/km［1］，就需要建立地方独立坐标系。利用高程归化和高斯投影对于控制网边长的影响具有前者缩短和后者延长的特点，如果两者不能完全抵偿而允许有一个残余的差数VS，则其相对差数为

由式(1)可知，由于高程归化投影变形与高斯投影变形符号相反，所以在一定的区域内，两种变形可以相互抵偿，这就需要采用一种行之有效的办法，即建立独立坐标系。

二、独立坐标系的建立方法

一般的，根据式(1)的计算，当 ym值不小于45 km或 Hm在 160 m以下时，投影变形值小于2.5 cm/km。对于投影变形超限的测区，根据地理位置和平均高程独立坐标系的建立方法一般有3种:选择合适的中央子午线(即改变ym以抵偿由高程面的边长归算到参考椭球面上的投影变形)，选择合适的投影面(即改变Hm以抵偿由高程归化引起的变形)和两者均选定。建立地方独立坐标系有3个必要参数:中央子午线、投影面及地方坐标系参考椭球。通过对地方坐标系参考椭球几何元素、定位及定向的确定，使得椭球面与投影面拟合最好，这样投影变形可以减到最小，同时要求便于与国家坐标系统进行换算。

三、投影面变换的方法——椭球膨胀法

椭球膨胀法的基本思想是保持参考椭球的定位和定向不变，对椭球进行缩放，使得经过缩放之后的参考椭球的椭球面与独立坐标系所选定的平面相切，在切点处，两椭球的法线重合。要满足上述缩放条件，新椭球的长半轴 a1和扁率 α1分别为［2］

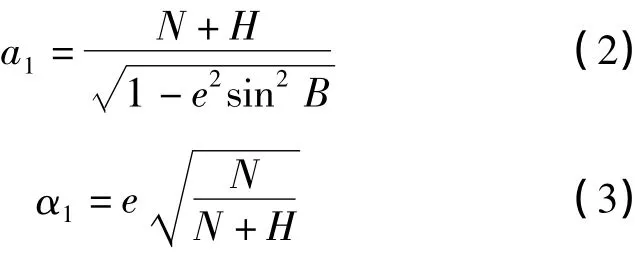
式(2)、式(3)中，N为卯酉圈曲率半径;B为大地纬度;H为投影面大地高;e为原椭球的第一偏心率。通常，采用膨胀后椭球与原椭球的中心保持不变，方向保持不变，椭球扁率保持不变(即da=0)。这种观点易于实现，而且能保证成果精度满足要求。椭球膨胀法有多种方法实现不同投影面的坐标转换，在工程实践中多采用如下3种方法［3-4］:

1)椭球长半径的改正量为投影面大地高H(da=H)。

2)投影面的大地高H等于卯酉曲率半径N的变化量(ΔN=H)，又由

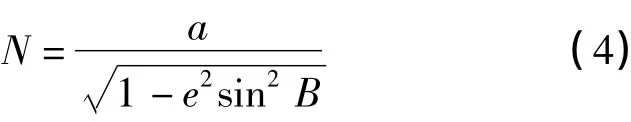
得出

3)以基点上参考椭球的平均曲率半径的变化值求出椭球长半径的改正值。设R0为测区中心在国家参考椭球下的平均曲率半径，R'0为独立椭球下的平均曲率半径，又根据平均曲率半径公式

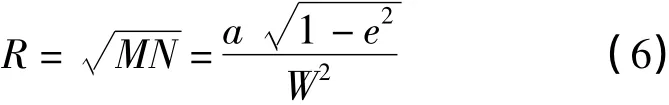
得到

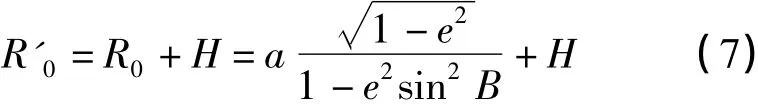
即

四、换算方法

由莫洛金斯基公式可求得国家控制点的大地坐标系转换到独立坐标系中的计算公式为［5］

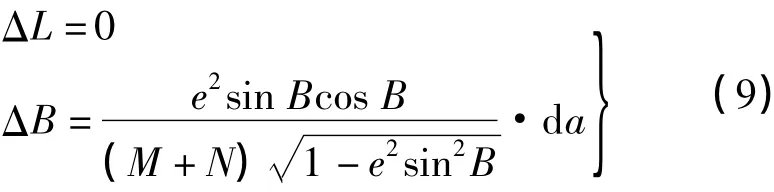
式中，

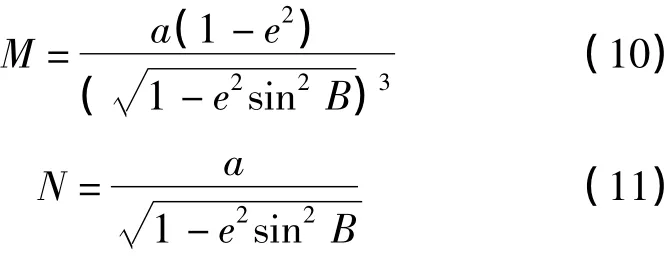
其中，M为国家参考椭球子午曲率半径。由此实现椭球膨胀法的算法流程为:首先确定项目中心区域的B和L;其次确定高程异常ζ，与投影高程面的正常高相加，进而确定投影面的大地高H;然后再将投影面大地高按上述3种方法的其中一个进行计算，得到地方参考椭球的长半径a，将已知控制点在国家坐标系下的平面坐标进行高斯反算得到其大地坐标;由式(9)计算ΔB，从而得到在地方独立坐标系中的大地坐标;最后根据地方参考椭球的椭球参数，进行高斯投影正算。

五、采用TGO软件实现独立坐标系的建立

某山区平均纬度为40°47'，测区平均高程为300 m，平均高程异常为17 m。测区已有1980西安坐标系(117°)起算点 4个。现以中央子午线118°30'、测区平均纬度及平均高程面建立地方独立坐标系。控制网中起算点成果如表1所示。

表1 起算点国家坐标系成果表(1980西安坐标系，中央子午线117°)

1)a1=a+H，得到独立参考椭球长半轴为6 378 457 m。过程如下:

打开TGO坐标系统管理器，新建地方独立坐标系统DF1-118.30，即椭球长半轴为6 378 457 m，扁率不变，中央子午线设置为118°30'，中心纬度为0，纵轴加常数为0，横轴加常数为500 000，尺度比为1。然后打开国家坐标系二维约束平差控制网项目，将坐标系统改变为DF1-118.30，此时，各点的平面成果已是该地方独立坐标系下的坐标值。各起算点地方独立坐标系成果如表2所示。

表2 独立坐标系成果(椭球长半径改正量为投影面大地高，a1=6 378 457 m)

2)投影面的大地高H等于卯酉曲率半径N的变化量。计算公式通过VB或Excel可轻松实现，以Excel为例，计算情况如表3所示。

表3 椭球膨胀法2中曲率半径变化量的计算过程

可知独立参考椭球长半轴为6 378 456.547 m。打开TGO坐标系统管理器，新建地方独立坐标系统DF2-118.30，椭球长半轴为6 378 456.547 m，其余项设置及操作方法同方法1)。各起算点按方法2)计算出的独立坐标系成果如表4所示。

表4 独立坐标系成果(投影面的大地高H等于卯酉曲率半径N的变化量，a1=6 378 456.547 m)

3)以基点上参考椭球的平均曲率半径的变化值求出椭球长半径的改正值，利用Excel进行椭球膨胀法3)计算的计算过程如表5所示。

表5 椭球膨胀法3的计算过程

可知独立参考椭球长半轴为6 378 457.159 m。打开TGO坐标系统管理器，新建地方独立坐标系统DF3-118.30，椭球长半轴为6 378 457.159 m，其余项设置及操作方法同方法1)、方法2)。可得各起算点按方法3)计算出的独立坐标系成果如表6所示。

表6 独立坐标系成果

4)通过TGO中的当地点设置来实现。以椭球膨胀法3为例新建项目，将项目属性由默认改为1980西安坐标系(XIAN80-117)，然后点击当地点设置，如图1所示。

图1 当地点设置界面

高度为317.159 m，即椭球长半轴变化量(根据选择膨胀法不同，数值不同)，选择使用地面坐标和用投影位置计算比例尺选项。将表6中的地方椭球大地坐标导入到项目中，得到的网格坐标即为独立坐标系平面坐标，如表7所示。

可见，方法4)与方法3)的结果一致。对控制网进行无约束平差后，以表7坐标为起算数据，在该独立坐标系的基准下进行平差计算，就得到了控制网独立坐标系成果。

表7 独立坐标成果(采用当地点设置并基于方法3)的地方椭球，a1=6 378 457.159 m)

六、结 论

1)椭球膨胀法其实是不同基准间的转换，虽然投影时的椭球参数与国家参考椭球的参数有所差异，但经投影后所得平面坐标在数值上与国家参考椭球的椭球面上的平面指标接近，两者有着较严密的换算关系，易实现转换。ΔΒ与da有关，采用3种方法计算da会有3种不同值，则ΔB亦有3种成果，每一种椭球膨胀法采用上述的两种计算方式所得结果是一致的。3种椭球膨胀法计算的坐标值虽然不同，但在坐标间的相对关系上是基本一致的。

2)在建立独立坐标系统时，投影带和投影面的选择尤为重要。对于平坦的测区，距国家3°带中央子午线小于45 km的测区，投影面一般可选平均高程面;否则应选取抵偿高程面。如果测区高程起伏相较大，可通过变换中央子午线位置与投影面高程值来实现，或是分带计算(多见于线状工程测量)。

3)通过对TGO中的坐标管理器及当地点设置的操作，可以很好地解决投影面坐标转换问题，更方便建立独立坐标系统。

［1］ 李征航，黄劲松.GPS测量与数据处理［M］.武汉:武汉大学出版社，2007.

［2］ 北京市测绘设计研究院.CJJ 8—99城市测量规范［S］.北京:中国建筑工业出版社，1999.

［3］ 施一民.现代大地控制测量［M］.北京:测绘出版社，2003.

［4］ 施一民.建立区域坐标系问题的我见［J］.测绘工程，2000，9(1):38-41.

［5］ 冯林刚.GPS测量控制网纳入独立坐标系的方法［J］.地矿测绘，2000，16(3):6-8.

［6］ 邱云峰，倪津.不同投影归算面间的坐标换算［J］.测绘通报，2001(9):12-13.

［7］ 畅开狮.建立城市独立坐标系相关问题的探讨［J］.城市勘测，2008(1):86-90.

The Establishment of Independent Coordinate System Based on the Ellipsoid Expansion Method

YU Yajie，ZHAO Yingzhi，ZHANG Yuehua

0494-0911(2011)12-0033-04

P226

B

2011-11-04

于亚杰(1982—)，男，河北保定人，工程师，主要从事控制测量方面的工作。