基于球结构支持向量机的QuickBird影像分类分析
2011-11-15杨敏华
林 超,杨敏华
(中南大学 信息物理工程学院,湖南 长沙 410083)
基于球结构支持向量机的QuickBird影像分类分析
林 超,杨敏华
(中南大学 信息物理工程学院,湖南 长沙 410083)
在支持向量机多类识别基础上探讨以球结构替代传统超平面支持向量机对QuickBird影像进行分类的可行性,对重叠区域的数据分类采用新规则,提高球结构支持向量机算法的泛化性能,并将分类结果与最小距离法、最大似然法分类结果进行比较,实验结果表明该算法有效可行,降低了二次规划的复杂度,缩短了样本训练时间。
支持向量机;核函数;超球;多类分类;重叠区数据
近代遥感起源于20世纪60年代,到80年代高光谱遥感技术兴起,遥感分类是人们获取信息的一种重要的手段[1]。光谱遥感影像分类一般分为监督分类和非监督分类,最常用的监督分类法是统计分类法,包括最大似然法、最小距离法和平行六面体法。其中最大似然法的分类精度和稳定性为最佳,但是该方法的缺点在于:①假定每类的特征向量在特征空间中服从正态分布;②为了准确地估计分布参数,需要大量样本,而且随着波段数的增加,样本数也要求迅速增加。
为了解决有限样本的学习问题,Vapnik等在20世纪70年代建立了统计学习理论(Statistical Learning Theory,SL T)的基本体系,该理论第一次强调了小样本统计学习的重要性[2]。
1 支持向量机
支持向量机(Support Vector Machines,SVM)是基于统计学理论发展起来的,核心思想是把样本非线性映射到高维特征空间(甚至是无穷维空间),以结构风险最小化为归纳原则,在高维空间中构造具有低VC维的最优分类超平面作为判决面,使分类风险上界最小,从而使学习机器具有最优的推广能力[3]。
SVM的基本理论本身是用来解决两类问题,不能直接用于多类分类,当前有许多算法将SVM应用到多类问题,这些算法统称为“多类支持向量机”(M ulti-Category SVM,M-SVM)。这些算法各有优缺点,但都没有脱离最优超平面思想,将他们应用于遥感影像分类问题上并不甚理想,总体来讲,都面临如下问题:①处理数据规模有限;②算法复杂性高;③不易于扩充[4-5]。
球面支持向量机是将超平面用球面替代,试找到一个能包含某类全部(几乎全部)样本的支持向量所构建的超球面,对于单类数据要求这个球面将球内外样本尽可能正确分开,并且超球的半径尽可能的小[6-7];在解决多类问题上文献[8]提出一个球结构的支持向量机,该算法的二次规划计算量小,容易推广和扩充[9]。
目前,针对遥感影像数据进行分类还是仅局限于传统的分类方法,在高光谱影像分类时更是运算速度慢、分类精度低,而且出现了严重的 huges现象。本文分析了球结构SVM在QuickBird多光谱影像分类中的应用,建立球结构分类模型,实验验证该分类器用于QuickBird影像分类有效可行,处理数据容量大大增强,算法复杂性较小,但分类精度有待进一步提高。
2 球结构支持向量机基本算法
假定现有N个m维空间的元素集合:Ak,k=1,2,…,N,每个 Ak包含lk个点 xik,i=1,2,…,l;这些点属于同一分类,对于每个 Ak,寻找一个球(ak,Rk),其中,ak表示球心,Rk定义为球的半径的平方,使得在 Rk尽可能的达到最小的情况下球(ak,Rk)包含所有(或者几乎所有)样本点 xik,引入松弛变量ξk,得到约束条件
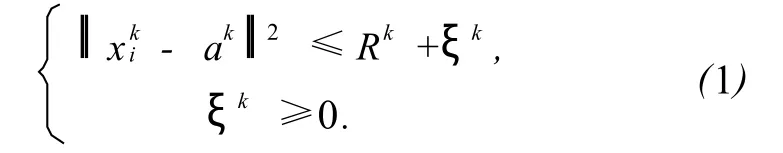
由 minξk,min Rk得到目标函数 F(Rk,ak,ξk)=Rk+Ck∑iξk。其中 C为惩罚因子,用于控制对错分样本惩罚的程度,实现球的大小和错分样本之间的折衷。由 K-K-T条件,得到拉格朗日函数
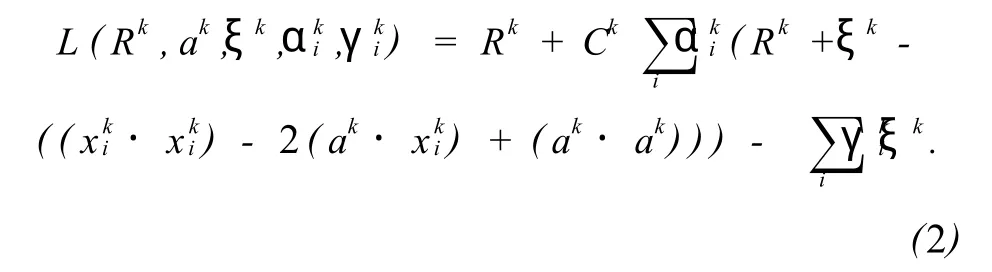
其中 ,γki≥0,ξk≥0,为 Lagrange乘子。
通常情况下,即使排除了偏远的样本点,数据依然不会呈现球状分布。为了使算法适用于更广泛的领域,采用同常规SVM方法类似的核函数方法,把样本变换到更高维的特征空间,在变换空间中求最优超球面[10]。理论已经证明,只要核函数 k(x,y)满足Mercer定理,核函数就可以表示为高维空间中的2个向量的内积。通常采用高斯径向基核函数(RBF)。
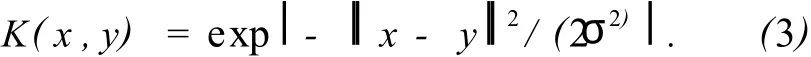
由式(2)将问题转换为对偶问题,并用核函数K(x,y)代替高维空间中的2个向量的内积,这样求最小球的二次规划问题即为
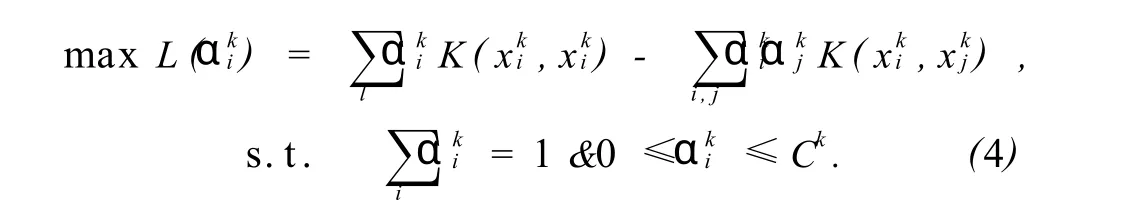
对每一个分类都求解如上所述的二次规划问题,产生 N个球,每个球代表一类,而球面上的点就是所对应的支持向量(称为球支持向量)。这样对于给定一个样本点 x,计算这一点到球心的距离的平方,根据就近原则判定样本点分属类别,得到如下决策函数:
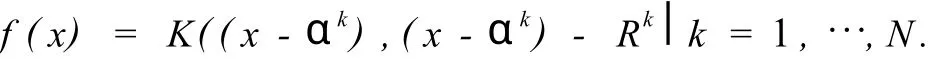
找出最小的 ft(x),则 x属于第t类样本点集合[5]。
3 多光谱遥感影像分类实验
3.1 QuickBird影像数据
实验采用4个波段的QuickBird影像作为分类对象,遥感影像数据由DigitalGlobe公司于2006年采集,位于乌海市境内,影像大小为815×828(见图1);参考影像选取分辨率较高的同一位置全色波段遥感影像,大小为3 260×3 312(见图2)。分类区域处于城郊结合处,有影像可以看出左面为大面积的荒地,植被覆盖较少,多为容易生长的灌木林,右面为部分城区影像,建筑密度较高,带状公路由城区通往郊外。现结合实际情况将该区土地利用粗分为道路(A)、居民建筑(B)、荒地(C)、灌木林(D)和绿化植被(E)5大类,选取各类训练样本各150个,选取道路测试样本602个,居民建筑测试样本618个,荒地测试样本627个,灌木林测试样本400个,绿化植被测试样本350个;借助于 ENV I软件的相应功能模块,对球结构支持向量机进行遥感影像分类的可行性进行验证,分析分类效果。

图1 多波段遥感影像图(RGB:3,2,and 1)
3.2 分类结果及精度分析

图2 全色波段遥感影像图
实验分别采用最大似然法、最小距离法、球结构支持向量机对影像进行分类,将球SVM与经典监督分类算法(M inimum Distance,Maximum L ikelihood)做比较分析。
1)ENV I软件下的classificationsupervisedM-inimum Distance和M aximum Likelihood对影像分类,分类结果如图3、4所示;
2)基于球结构SVM的QuickBird影像分类算法。主要过程为:特征选择和提取,数据处理,确定惩罚因子C=1 000,RBF核函数参数σ=1.50,选择RO I,分类处理。对球结构SVM算法来说,理想情况下任意两个超球都相互确定,那么所有样本都能正确分类,但影像中可以看出,不同的类别可能具有相似的光谱特征,会导致部分样本类别之间差异不明显,出现两个或者多个超球重叠的情况,预测点分类归属不确定,导致整个分类精度下降。为解决这个问题,利用一个简单有效的重叠区归属判别方法:由常规SVM分类方法可以得知,在点 x到2个分类球的距离相等的情况下,这个点更有可能属于大球所属的类别,分类球的大小对分类具有较大的影响[11-12],具体算法如下:

3.3 分类结果评价
实验用总体精度(OA)、kappa系数(见表1)作为精度评价指标,由分类结果可以看出,最大似然法的分类精度最高,城区的道路及居民建筑的大致走向可以清晰识别;最小距离法分类精度三者中最低,利用球结构SVM进行遥感分类是可行的,其分类精度比最大似然法略低,居民建筑和道路、灌木林和绿化植被混淆的情况较严重,分析原因在于:①训练样本的选取不够有效;②分类时出现较多的重叠相交区域,在运算时重叠区域的样本点的分类策略将影响算法的分类精度,对预测点的归属判别出现错分情况;③算法仍然存在不足之处需要改进。另外,球结构SVM二次规划计算量较小,能处理大容量数据且算法复杂性较小,训练时间缩短,有很好的扩充空间。

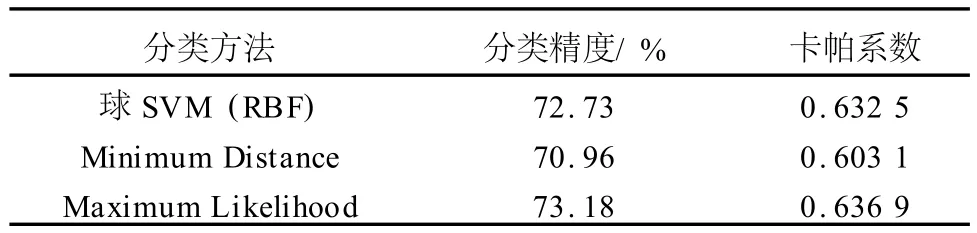
表1 不同分类方法的精度值与kappa系数
4 结 论
对超球重叠区域的数据正确分类对球结构支持向量机的分类性能至关重要,实验验证了球结构的支持向量机进行多光谱遥感影像分类的可行性,降低了算法的二次规划的复杂性,训练时间缩短,但分类的精度相较于一些经典算法并没有提高,利用球结构SVM处理遥感影像数据在以下方面还有待进一步深入研究:
1)进一步缩短分类时间,如果预测样本在球结构中出现频繁相交的情况,那么分类的时间将延长很多,精度降低,寻找一种改进的算法对重叠区域的样本进行分类,有利于分类精度提高和速度提升;
2)球内部的支持向量实际上对球分类器的构造没有实际意义,但仍然参与运算,降低了运算速度;
3)采用RBF核函数是以牺牲训练时间为代价,要进一步提高参数选取的速率;
4)研究改进球结构支持向量机,现在国内外很多文献讨论了球结构支持向量机的改进算法,提高算法的适应性,寻求最优方法解决遥感影像多类分类的精度问题值得深入研究;
5)本次实验只是进行一般的粗分类,还不具备实用的条件,下一阶段进一步实验将球结构支持向量机运用于高光谱遥感影像分类,探讨其可行性及精度评价。
[1]浦瑞良,宫鹏.高光谱遥感及其应用[M].北京:高等教育出版社,2000.
[2]刘志刚.支撑向量机在光谱遥感影像分类中的若干问题研究[D].武汉:武汉大学,2004.
[3]许磊.支持向量机和模糊理论在遥感图像分类中的应用[D].无锡:江南大学,2006.
[4]李斌.基于多组合分类器的高光谱遥感图像识别技术研究[D].北京:中国地质大学,2008.
[5]郭雪松,袁治平,刘波.半模糊超球支持向量机多类分类方法研究[J].中国管理科学,2008,16(2):140-144.
[6]TAX D.,DU IN R.,Support vector domain descrip tion.Pattern Recognition Letters,1999.
[7]TAX D.,DU IN R.,Data domain descrip tion by suppo rt vectors.In Proceedings of ESANN99,ed.M Verleysen,D.Facto Press,Brussels,Baldonado,M.,Chang,1999:251-256.
[8]朱美琳,刘向东,陈世福.用球结构的支持向量机解决多类分类[J].南京大学学报:自然科学版,2003,39(2):153-158.
[9]刘爽,史国友.基于加权超球支持向量机算法的超文本分类研究[J].大连海事大学学报,2009,35(1):71-74.
[10]吴强,贾传荧,张爱锋,等.球结构支持向量机的改进算法及仿真研究[J].系统仿真学报,2008,20(2):345-348.
[11]袁胜发,褚福磊.球结构支持向量机在转轴碰摩位置识别中的应用[J].振动与冲击,2009,28(8):70-73.
[12]徐图,何大可.超球体多类支持向量机理论[J].控制理论与应用,2009,26(11):1293-1297.
QuickBird image classification analysis based on sphere support vector machine
L IN Chao,YANGM in-Hua
(Institute of Information Engineering Physics,Central South University,Changsha 410083,China)
After summarization of SVM for multi-class recognition,it analyzes a method of sphere support vecto r machine w hich takes p lace of traditional SVM for QuickBird remote sensing image classification;p resents a new classification fo r intersection data w hich lesds to a better generalization accuracy and compares it w ith M inim um Distance classification,maxim um likelihood classification methods.Experimental results show the method is feasible,and reduce the comp lexity of quadratic p rogramm ing and sho rten the training time.
support vectormachine;kernel function;hypersphere;multi-class classification;intersection data
TP751.1
A
1006-7949(2011)03-0046-04
2010-10-28
林 超(1985-),女,硕士研究生.
[责任编辑刘文霞]
