椭球面上混合基线图形的缓冲区和等比例线问题
2011-11-15吴艳兰
胡 海,吴艳兰
(武汉大学 资源与环境科学学院,湖北 武汉 430079)
椭球面上混合基线图形的缓冲区和等比例线问题
胡 海,吴艳兰
(武汉大学 资源与环境科学学院,湖北 武汉 430079)
分析基于海洋基线的一般图形状况下,既适合国家法定且公布的各“直线基线”情况,又适合国家法定且公布的各“正常基线”情况的缓冲区和等比例线问题。指出在地球椭球上计算它们的复杂性,概括在这一困难工作上技术现状,分析流行的WL&W T方法在这一工作上的不足,最后,介绍地图代数相应算例。
基线;缓冲区;等比例线;椭球
《联合国海洋法公约》[1]指出了非常重要的海上划界的基本量算基准—基线。领海、毗连区、专属经济区、大陆架均由它们作为基准起量。它们实际包含了表现在海图上的曲折的海湾曲线作为“正常基线”和国家法定且公布的各“直线基线”的组合,这样,绝大多数海洋国家可作为混合基线图形,这是一般化广义的情况。在边界谈判中,只通晓或适用于一种基线制,而不通晓或适用于各相关国家其它种基线制,难以科学而公正地维护国家权益。
法律的法理基础是科学、公正、公平。由于历史原因,国际法中上述“直线基线”的提法,在地球科学中是不够确定的,也引起学术界广泛的注意,因为在地球曲面上实际并不存在欧几里德空间(Euclidean Space)的直线,都是空间曲线,而所指若是在海图上,则由于墨卡托(Mercato r)地图投影的多样性,两点间的直线也具有多样性和不确定性,只有在正切圆柱M ercato r投影的海图上才具有唯一性,但是广泛使用M ercator投影海图上两基点间的同一直线对纬度不同高低的国家实际是有偏的,如图1所示,它并不重合于真正无偏的两点间最短程线。实际上“直线基线”概念是由各国家自己解释,并由相关国家承认或据理反驳及协商确定。这种多义的解释,也引起严密技术解决的复杂性(见表1)。

图1 等角航线偏向低纬
划分权益界线首先要明确问题产生和解决的度量空间,采用该空间的尺度度量来解决问题;二是不管是正常基线或是直线基线,以一般二维复杂度量空间中的一般曲线才可以概括本文所讨论问题的诸多图形。

表1 海洋划界中的科学问题及解决现状
1 自然图形的中轴(或中间线)和缓冲区问题一般解是几何学上的困难问题
自然图形的中轴(或中间线)问题是一个重要的几何问题,它包含着很多基础的重要的应用。在二维空间中按图形是:①离散点;②或折线段;③或多边形;④或一般曲线段、或一般曲线多边形;⑤或者它们的组合,该问题呈现出不同的复杂度层次。
1)在欧氏度量空间,已有两离散点间中轴、两相交直线间中轴、已知一函数曲线与一定点间中距线等在经典的平面几何、解析几何中都已有理论上可靠和技术上实用的方法;1976年,Shamos和 Hoey有效计算平面离散点集的中轴结构——Voronoi图诞生了计算几何[2],相应也产生了简单多边形的中轴算法。对于数个离散点、折线和多边形组合情况,问题徒然呈现困难,尚未见统一且严密的算法,而对于两确定函数曲线(尤其是曲线段)间的中距线至今尚没有通用可靠的方法,复杂的组合情况更是如此。
2)实际的自然曲线段不仅包含了各种函数曲线段,而且包含了它们的各种连续组合,并且实际的自然曲线段最一般地是以数字化的形式或者说是以数值形式出现的,以函数形式表达它们(以便使用代数法),还要经过函数逼近或拟合过程,既复杂又丢失精度,最好应直接使用几何方法,而解决此几何问题的直接几何方法也尚未见,相应的,解决二维一般解问题的直接几何方法也尚未见。
3)地球科学中实际几何问题基本上应当考虑在旋转椭球体的度量空间中解决,尤其是中、大区域和全球性问题,海洋划界实际上都是这类问题。这对地球科学的新兴综合性学科——地球信息科学是具有基础意义的。这问题至今没有通用可靠的方法。
2 现今所用海上划界技术方法的进展和分析
海上划界问题最典型地表明在地球信息度量空间中精密空间分析重要性和必要性。
综上所述,目前划界技术中所涉及的相应科学问题及其解决现状,见表1。
表1把地球上混合基线图形的缓冲区和等比例线问题归纳为 E2和地球椭球面上宽度L的缓冲区、等距离线和等比例线3种空间分析问题。所谓等距离线就是线、面图形的Voronoi图,等比例线相应就是加权的Voronoi图,L为12、24、200 nm的缓冲区与国家基线的V图的交集就是国家领海、毗邻区和专属经济区。同样,200 nm之外,则还有所辖大陆架区(还要考虑海底地形特征)。表中 E2平面下直线基线的多边形中轴,其数学上解法可见[3],它实质就是平面几何中角平分线的组合,并可扩展为加权距离。这种等距离(比例)线是严密的。相应的,对于 E2平面下一般曲线可化为折线近似求解外尚无良法,这时仍为“多边形中轴”类的解,但从几何性质而言,有一定差别。化曲为直,问题简化,但有些性质突变,有后遗症,如尖点和新结构线产生,并需较大范围讨论误差。而在地球椭球体面上,传统矢量方法由于度量空间定义、复杂图形的定义、尺度定义的变化而十分复杂,原有的方法往往很难继续使用。图2[2]显示了地球椭球体面上一个点的缓冲区状况,一个复杂图形缓冲区的“包络”及相互在空间中的分界线—Voronoi图,理论和实践上都是较困难而不易计算的。
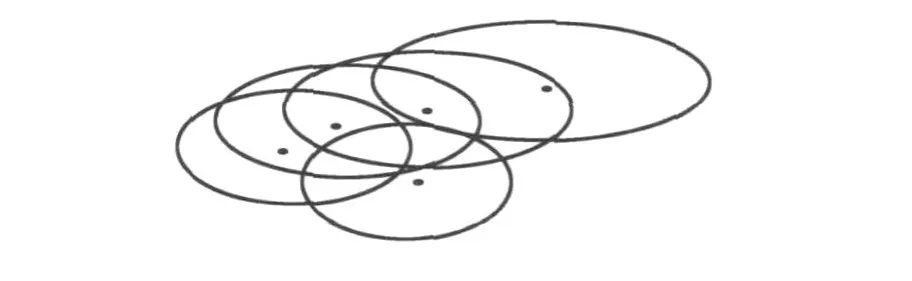
图2 地球椭球体上点群所形成的缓冲区
这里所有基线都可以是一般曲线的子集,并可以后者概括。一般曲线问题解决了,子集轻松解决,因此,海洋划界的科学问题可概括为:“椭球面上混合基线(或一般曲线)图形的缓冲区和等比例线问题”,这椭球面自然也包括球面特例。
3 WL&W T方法剖析
WL&W T方法是针对正常基线,被认为由手工描绘海域水线的方法演变来的新方法[2,4-5],它的思路是对分属各国的大陆和海岛边界各离散节点串配赋标识码,然后以一定的步长求它们外侧在平面上或椭球上的平行线,当不同国家的平行线有交叉时,求出其交点。为提高精度,通过在交叉附近不断缩小步长来逼近交点,如图3所示,最后,顺序连接这些交点得到等距离线或中间线。文献[4]认为“此方法无法提供等比例线生成的能力”,另外,由于计算量很大,算法的实时性较差。
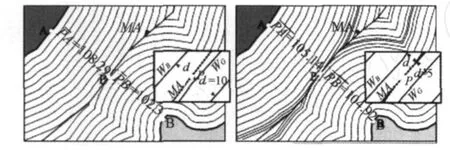
图3 WL&WT方法中中间线生成原理[5]
4 地图代数的解决方案
地图代数长期研究始终是以这一问题的实际解决作为目标之一。它是以定义了距离函数的规则栅格点集及其变换和运算来进行空间分析[6]。它作为“一种新的理论与技术基础”图形的Voronoi图、障碍Voronoi图、地球尺度空间的Vo ronoi图等理论研究,丰富了近代几何的成果[7]。”从理论角度而言,地图代数研究实际上已尽力实施了本主题的可行性研究,它本质上通过距离变换计算并标绘出每一栅格在标定度量空间的对于最近实体对象的距离。已经完成了表1中已有和所缺少的各种方法的研究,并复盖了表1,是一个统一的全局性解决方案[6]:①它以问题提出和解决的度量空间的严密度量为基础,并且海上划界必须以国际标准的椭球体、大地坐标系、该椭球体大地线尺度三者为基准的地球信息度量空间来度量和实施[8-9];②它以最一般的自然图形作为分析和计算对象,由于各种实际基线十分复杂,因此,把它作为一种确定的任意复杂曲线,它是由点、线、面组合而成,并冠以混合基线代表之以实现科学计算;③它以矢、栅状况下的最高分辨率相应间距作为度量单位,这就为各种点集计算提供了可选的、可信的、不大于1/2分辨率相应间距的误差;④为双方、三方及任意多方,为协商确定后的各相应比例,准确划分相应中间线、比例线准备了科学计算的现实能力,主要是下列定义:定义海上划界的距离为大地线距离;定义点 a到点集B距离d(a,B)=min d(a,b),b∈B;定义点集 A的L宽缓冲区为到A距离大于0且不大于L的点集;定义点集A、B间比例(k)线为所有到 A、B距离之比为k的点集,而中间线为k=1∶1的比例线特例。
地图代数已严密地实现了上述计算,其中L、k均可为实际可能的实数。因为实际区域计算往往十分敏感,故有时采用欧氏距离对几何图形作示例,如图4~6所示,它例示了各种曲线及各种相互比例状态下的比例线。

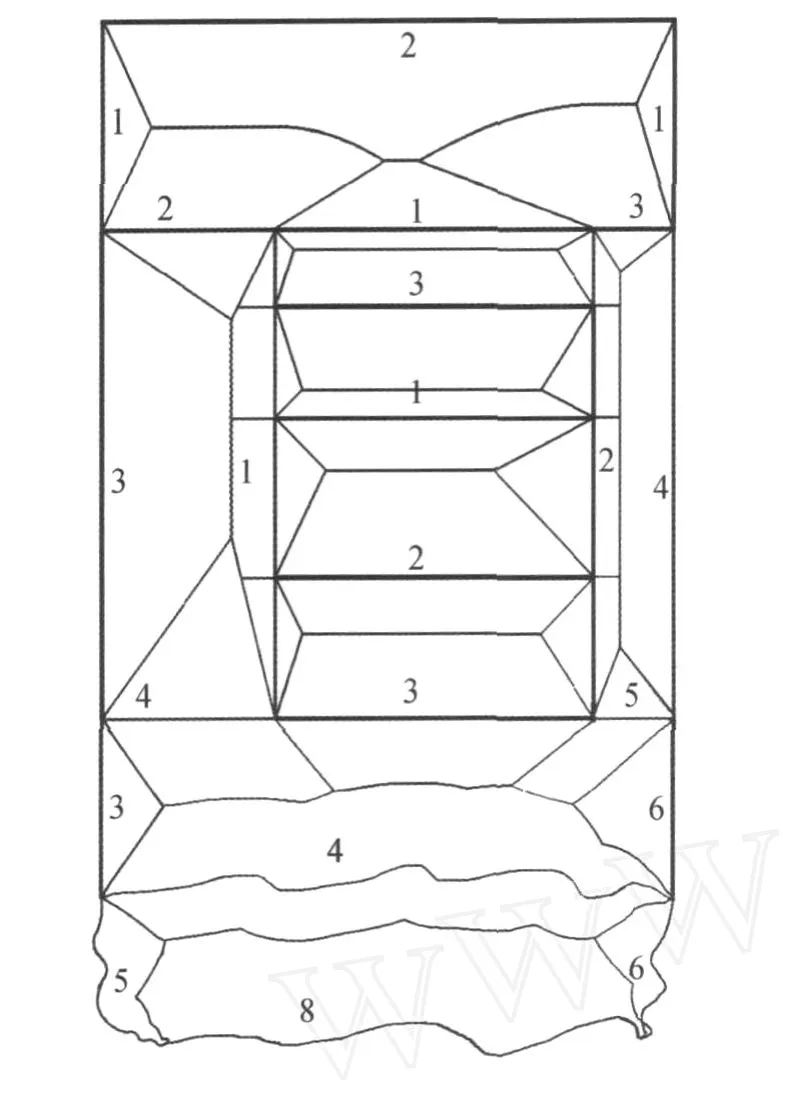
图6 原图的 V图(向内)
图7、图8所示为 WL&M T方法计算中间线的例图及地图代数方法的复算图叠合效果,图9、图10为文献[9]计算的科威特和沙特阿拉伯之间的Salw a海湾中间线,以及地图代数方法的复算图叠合效果。可以看到,它们几乎是完全重合的,初步说明了地图代数方法的计算能力及良好的适应性。
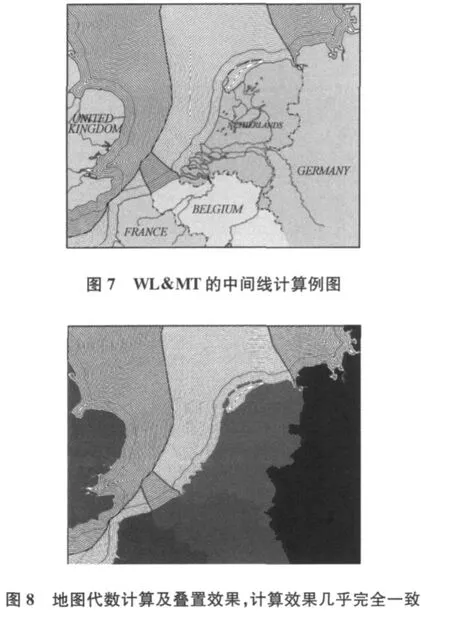
并且还初步考虑了不等权状况和空间具有障碍等情况。但是对重大系统性问题、切实地全面解决则尚有极大量的工作。

[1]联合国第三次海洋法会议.联合国海洋法公约[M].北京:海洋出版社,1992.
[2]周培德.计算几何[M].北京:清华大学出版社,2001:13,212-235.
[3]彭认灿,王家耀.基干地球椭球体的缓冲区构建技术研究[J].测绘学报,2002,31(3):270-273.
[4]彭认灿.海洋划界 GIS技术研究和实践[D].郑洲:信息工程大学,2003.
[5]Albert H.J.CHRISTENSEN,A Fully Automated Sea Boundary Delineato r FIG XXII International Congress,Washington,D.C.USA,2002:19-26.
[6]胡鹏,游连,杨传勇,等.地图代数[M].武汉:武汉大学出版社,2002:117-165,268-292.
[7]胡 鹏,吴艳兰,杨传勇,等.大型 GI与数字地球的空间数学基础研究[J].武汉大学学报:信息科学版,2001,26(4):296-302.
[8]胡鹏,胡毓钜,杨传勇,等.我国地球空间数据框架的设计思想、技术路线及若干理论问题的研究[J].武汉大学学报:信息科学版,2002,27(3):283-288.
[9]Gérard COSQUER and Jean-François HANGOUËT Delimitation of Land and Maritime Boundaries:Geodetic and Geometric Bases FIG Wo rking Week 2003,Paris,France,2003:13-17.
Problems of graphics buffersand the proportion line of ellipsoid m ixed baseline(or normal curve)
HU Hai,WU Yan-lan
(School of Resource and Environment Science,Wuhan University,Wuhan 430079,China)
The paper analyzes the graphic based on the general situation of the marine baseline buffer and under the p roportional line p roblem s.Pointed out that the earth ellipsoid to calculate their comp lexity,summarizes the technical wo rk in this difficult situation,sho rtcomings of the popular method of WL &W T in this wo rk,and finally describes the co rrespon ding map algebra examp les.
baseline;buffers;p ropo rtion line;ellip soid
P282
A
1006-7949(2011)03-0001-04
2010-12-14
国家自然科学基金资助项目(40701155,40571124);国家863计划资助项目(2009AA 12Z224)
胡 海(1977-),男,副教授,博士.
[责任编辑刘文霞]
