不同承诺能力下可耗竭资源的最优消耗*

周 伟 武康平

(清华大学经济管理学院，北京100084)

不同承诺能力下可耗竭资源的最优消耗*

周 伟 武康平

(清华大学经济管理学院，北京100084)

通过对可耗竭资源经济学的文献回顾，目前尚没有发现在可变时间偏好理论框架下探讨可耗竭资源的最优消耗等问题。该文尝试在双曲线贴现的可变时间偏好下，对一个可耗竭资源的纯消耗问题进行分析，讨论在不同承诺能力下资源的最优消耗速度及对资源的保护效果。模型结果证明，在国家的完全承诺能力下，资源的最优消耗速度最慢，选择的初始资源消耗最低，与时间偏好不变情况下的社会计划者问题等价。相反，在完全无承诺能力下，资源的最优消耗速度最快，选择的初始资源消耗最高，其短视的资源消耗行为必然会导致可耗竭资源的过度消耗。部分承诺能力下的情况则介于完全承诺能力情况与完全无承诺能力情况之间。因此，在双曲线贴现的时间偏好下，资源消耗的最优速度依赖于承诺能力，承诺能力的提高会导致更低的有效时间偏好率，从而导致更低的资源消耗速度和初始资源消耗。承诺技术纠正了人们的不耐心程度与短视行为，从而达到保护可耗竭资源的目的。

可耗竭资源;时间偏好;双曲线贴现;承诺能力

当今人们已认识到，有些资源一旦开发殆尽就永远无法再生，人类必须反思以往开发与使用可耗竭资源的行为方式是否恰当。从可持续发展的角度考虑，既要做到适度开发以保证经济社会对可耗竭资源的需求，又要避免掠夺性开采，在没有找到可替代资源之前，防止当代人过度开发利用而使子孙后代面临资源枯竭。为了让资源枯竭耗尽在新替代资源出现之后，人们想出了诸多方案。譬如，积极寻找新的矿藏，开发更有效的技术，用可再生资源替代可耗竭资源，调整生产过程和消费习惯以对可耗竭资源进行保护和节约使用等。该文基于最后一种方案，在更符合人类行为的可变时间偏好理论框架下构建动态一般均衡模型，来讨论可耗竭资源的开发与使用。由于承诺是纠正人类缺乏耐心、短视和自我控制能力不足问题的最广泛使用的技术，比如资源开采方式的改变与人们消费习惯的调整就可用承诺来解决，因此本文将采用承诺技术来纠正人类的行为偏差，通过在可变时间偏好框架中引入一个代表不同承诺能力的时间T，从社会计划者角度来探讨可耗竭资源的最优消耗。本文在 Dasgupta 和 Heal［1，2］所建模型的基础上，采用Barro［3］的方法，分析了在双曲线时间偏好下的可耗竭资源的最优消耗问题，不仅得到了时间偏好不变情况下Dasgupta和Heal在纯消耗问题中讨论的可耗竭资源的最优消耗速度(“吃蛋糕”问题首先由Hotelling［4］在1931年中讨论)，而且改进了原模型不能分析承诺对资源消耗路径影响的缺点，并进而分析了不同承诺能力下对可耗竭资源的不同保护效果。

1 可耗竭资源与时间偏好理论文献综述

早在1931年，经济学就开始关心可耗竭资源问题了，但直到20世纪70年代，对资源耗竭的理论研究才活跃起来。Hoteling的经典论文使用可耗竭资源的社会价值来判断该种资源的抽取方式的合理性，发现在完全竞争条件下的最优抽取路径等同于社会最优抽取路径，还发现资源垄断企业的垄断产出是次优的，并且特别倾向于资源保护。Stiglitz［5］证明，如果资源需求弹性随时间推移而递增(譬如，发现了替代品)，或者如果在资源抽取成本每单位是常数，但随着时间推移而递减(譬如，拥有了新的技术)的情况下，那么垄断者仍趋向于比社会最优情况下更加保护资源。纵观全球的资源性企业，他们一般由国家所垄断，这就为本文提出的可耗竭资源的开发利用应由社会计划者垄断以保护资源提供了理论依据。

可耗竭资源的开发利用涉及到人们的时间偏好。人们在进行选择时，总是希望尽早尽快得到收益，而不愿意推迟消费，其耐心程度呈现前低后高特征，因此人们的时间偏好应当是变化的。时间偏好反映在效用贴现率ρ上:ρ越大，消费的未来效用越小，人们的耐心程度也就越低，越愿意当前更多消费而不愿意推迟消费。但在新古典的最优增长和内生增长模型中，效用贴现率ρ都被当作常数看待。比如，Ramsey［6］认为在一个确定的世界里，效用贴现率应该为零，这意味着人们给未来效用和当前效用相同的权重。P.A.Samuelson［7］的指数贴现模型也将效用贴现率看成是固定的，很明显，指数贴现模型以完全理性人假设为前提的。对这种理想的贴现技术，Samuelson也承认这种设定没有理论依据，仅仅是为了计算上的方便。如何恰当设定贴现率ρ，便成了应当研究的问题。

20世纪80年代以来，随着实验经济学的兴起，人们开始运用高度控制的实验来推算效用贴现率，发现效用贴现率随时间推移而变化，呈现出先高后低的递减趋势。此外，Bauer et al［8］还研究了年轻人、穷人、农民和受教育程度低的居民，发现他们更容易表现出不一致的时间偏好，表现出较低的自我控制能力。他们很少去对消费进行承诺，造成了他们的储蓄率很低，积累财富过低。这种现象在Jones和 Rachlin［9］的研究中也得到了证实。

作为贴现率递减的一种结果，Laibson［10］得出了引人关注的关于时间偏好变化的拟双曲线贴现模型:U(t)=ut+βδs－tus，(0 ＜ β 1，0 ＜ δ＜ 1)(这里，β 可看成短期贴现因子，δ可看成长期贴现因子，β=1时，就是指数贴现模型)。他发现个人对于今天和明天的消费表现出极度不耐心，但对于未来选择却表现出更有耐心，例如对于今后第365天和第366天的选择就表现得基本无差异。Laibson用双曲线贴现模型，成功地解释了欧美发达国家普遍的过度消费行为。由于短期内人们极度缺乏耐心和自我控制力，双曲线贴现模型便能很好地模拟人们沉溺于当前诱惑而过度消费的特点。Laibson进一步指出，承诺(commitment)有助于纠正时间偏好不一致所带来的行为偏差(例如有人承诺去参加一场学术研讨会，以克服个人懒惰去致力于写一篇论文等)，从而抑制当期的过度消费。Ashraf et al［11］根据这个原理为菲律宾银行设计金融产品，确实显著地刺激了当地居民的储蓄。

总之，由于短视行为和缺乏自我控制力，人们消费的时间偏好是可变的，并且基本上可用双曲线贴现模型来模拟。通过引入承诺技术来纠正时间偏好变动引起的行为偏差，便可达到抑制过度消费的目的。这一点对于可耗竭资源的开发利用研究具有很大的启发性:在时间偏好可变的行为方式下，用承诺来纠正人类的行为偏差，便有可能获得可耗竭资源的最优利用效果，进而得出正确的资源保护政策和策略。本文的研究正是基于这种考虑。

2 承诺与可耗竭资源的最优消耗

可耗竭资源的最优利用对经济社会的可持续发展至关重要。依据双曲线贴现的可变时间偏好理论，如果对人们消费行为不加约束，将会造成对可耗竭资源的过度开采和消耗，危及可持续发展。采用承诺技术来纠正人们在消费中的短视和缺乏耐心等引起的行为偏差，便可能抑制过度开采和消耗，取得有益于可持续发展的效果。下面就来分析承诺对资源开发利用的作用，构建不同承诺能力下的资源最优消耗模型。

2.1 基本假设

在一个社会计划者经济中，国家垄断着资源开采。国家在考虑代际之间资源分配的公平问题时，为了达到可持续发展目标，是能够采用承诺技术来达到资源保护目的的。我国近期出台的十二五规划对稀缺资源的保护，充分展示了这一点。

假定可耗竭资源的当前存量为S0，时刻t的存量为St且St0。用Ci表示时刻t的资源消耗量，并假定资源的消耗等于资源的存量变化:S·t=－Ct。用u(C)表示资源消费的瞬时效用函数，从而人们在时刻t的资源消费效用为u(Ci)。假定u'(C) ＞ 0，u″(C) ＜ 0，且人们的时间偏好如双曲线贴现模型所述:

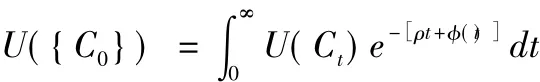
因此在效用最大化目标下，可变时间偏好的双曲线贴现模型可设置如下(不变时间偏好下的模型可参看［1，2］):

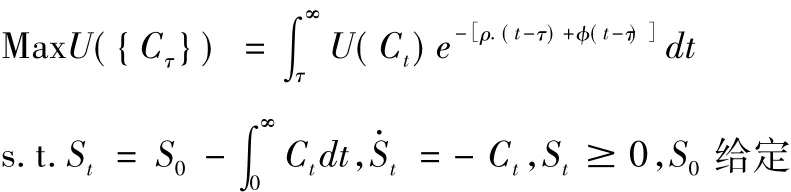
其中 ρ＞ 0， (t)0， (0)=0，且 (·)二阶连续可微， (ν) ＞ 0，n(ν) ＜ 0，以及lim0'(ν) →∞，lim '(ν) →0。ν→ν→∞则ρ+ '(ν)为ν时的瞬时偏好率。这些属性隐含了时间偏好率在近期高，但是随着ν的增长，瞬时偏好率渐进接近常数ρ，因此，本文所构建的模型是双曲线贴现的连续时间模型。另外，假设lcim0U'(Ct)=∞。定义相对风险规避系数t→，为简单起见，本文假定没有人口增长，效用函数为对数函数logu(Ct)，则有η(c)=1。

假定国家为了克服缺乏耐心、短视的资源消耗行为而向社会承诺，即在τ以后Τ的时期内承诺对资源的保护性开采，因此可由时间Τ的大小来衡量承诺能力的大小。如果Τ趋向于0，用ε表示一个无穷小的量，从而表示国家没有做出任何承诺，完全无承诺能力。当Τ趋向于无穷大时，表示国家对资源的保护性开采完全承诺，具有完全承诺能力。用介于这两者之间的Τ表示国家对社会的部分承诺，具有部分承诺能力。

2.2 完全承诺能力下的可耗竭资源的最优消耗

如果国家能以完全承诺能力的方式确定τ时刻以后的资源消耗，即在任意时刻τ选择资源的消耗路径以最大化未来的贴现效用和。由于在完全承诺能力方式下的资源消耗具有时间一致性，即当ν→∞， '(ν)→0，ν时的瞬时偏好率ρ+ '(ν)=ρ，此时又回到时间偏好不变下的情形，故仍可采用时间偏好不变的方法求解，因而根据最大值原理，Hamiltonian方程如下:

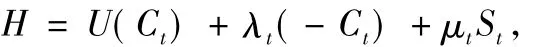
(其中λt，μt为拉格朗日乘子，μt＞ 0，μtSt=0)，从而可得出:

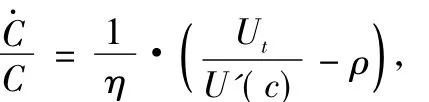
数为对数logU(Ct)，有 η(C)=1，从而

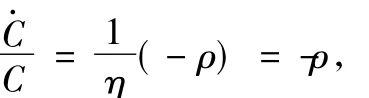
因此，可得出:

定理1:在双曲线贴现的时间偏好下，如果国家具有完全承诺能力，当效用函数为对数效用函数时，最优的资源消耗速度为ρ，初始的资源消耗C0=ρS0，(详情参见2.3节中的解释)，与时间偏好不变下的社会计划者问题等价。

2.3 完全无承诺能力下的可耗竭资源的最优消耗

由于国家对可耗竭资源的消耗完全没有承诺，因此，代表承诺能力的T→0，用ε表示这个无穷小的量。由于在可变时间偏好情况下，完全无承诺能力下的资源消耗具有时间不一致性，不能再采用最优控制原理来处理这类问题。在此，可利用动态规划的思想，来考虑完全无承诺能力时的国家对资源的消耗决策。当国家(即社会计划者)在时刻τ选择资源消耗Cτ时，这会影响到时刻τ+ε的资源存量 Sτ+ε，进而影响到时刻 τ+ ε 上的资源消耗量 Cτ+ε。因此为了决定资源消耗的最优路径C(t)，必须首先知道Cτ与Sτ+ε之间以及当tτ+ε时的Sτ+ε与Ct之间的关系。

现在假设国家在时刻τ选择了C(τ)的资源消耗，当ε→0时，由于在区间［τ，τ+ε］内Ct可看作不变，因此

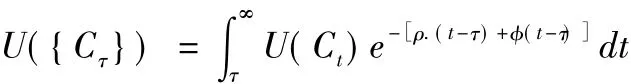
分写成两部分后有:

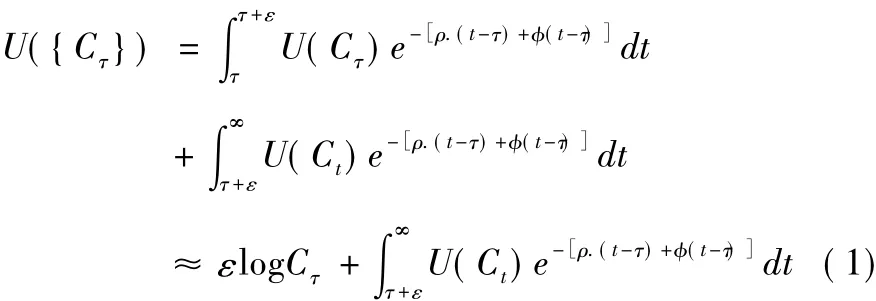
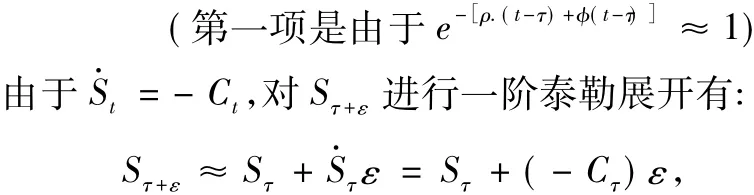
从而

现在先推测:在完全无承诺能力的情况下，可耗竭资源以λ0的增长速度进行消耗，即－λ0，(后面的推导将证明其推测成立)，从而可得到Ct=λ0St，(此过程的推导可采用猜解和待定系数法，先猜测Ct=ASt，然后两边对t求导比较后可知A=λ0，从而有Ct=λ0St)。因此当tτ+ε时，两边取［τ+ε，t］定积分后再对等式重排有

log Ct=logCτ+ε－ λ0(t－ τ－ ε)，

从而(1)可进一步写为:

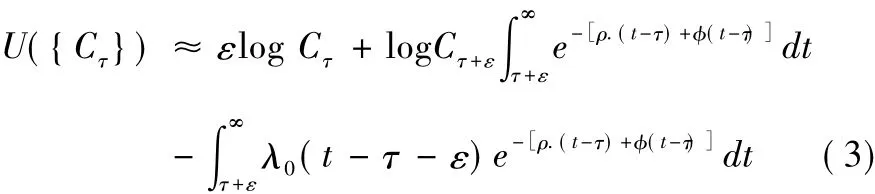
根据前面的分析，社会计划者(即国家)一旦选择了Cτ，就决定了Cτ以后的资源消耗路径，所以就(3)对Cτ求导有:

从而可得出λ0是瞬时偏好率ρ+ '(ν)的加权平均值，从而可知λ0是常数。由于 '(ν) 0， ″(ν) 0，以及当ν→∞， '(ν)→0，可以得出ρ λ0ρ+ '(0)。由此可得出:定理2:在拟双曲线贴现的可变时间偏好下，如果国家完全无承诺能力，当效用函数为对数效用函数时，最优消耗速，且介于［ρ，ρ+ '(0)］之间，初始资源消耗的选择为C0=λ0S0，其加权平均值越靠近区间右边，其消耗速度越快，初始资源消耗越高。与前面的完全承诺能力和后面的部分承诺能力比较，显然，在完全无承诺能力下，可耗竭资源的消耗速度最快，选择的初始资源消耗最高。因此证明了在双曲线贴现的时间偏好下，如果国家对资源消耗行为不加以承诺，其短期缺乏耐心、短视的资源消耗行为必然会导致可耗竭资源的过度消耗。

此外，从模型的构建中可看出，当对任意的ν有 (ν)=0时，此时又回到了时间偏好不变的跨期消费模型，(4)式可写为，从而可知在不变时间偏好情况下，国家在完全无承诺能力下的资源最优消耗速度为ρ，与有无承诺及承诺能力大小无关。因此，如果采用时间偏好不变的贴现率来模型现实的经济世界(本文讨论的是可耗竭资源的最优消耗)，则可能得不出政府想要保护可耗竭资源的政策，因为在这样一个理想世界里，资源的消耗速度已经达到最低。

2.4 部分承诺能力下可耗竭资源的最优消耗

对于部分承诺能力下可耗竭资源的消耗问题，可以用T(其中T＞0)来代替2.3节中模型的ε，重新求解上面的问题即可得到。由于

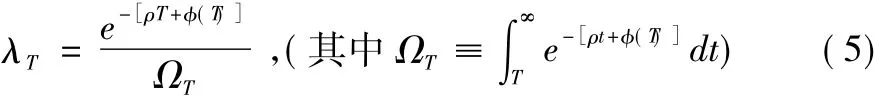
从(5)可看出，当T=0时，结果与完全无承诺能力时一致，由于资源消耗速度λT随着T从0趋向无穷大时单调递减，即从λ0降到ρ，从而ρ λTλ0。由此可得出:

定理3:在双曲线贴现的可变时间偏好下，如果国家有部分承诺能力，当效用函数为对数效用函数时，可耗竭资源的最优消耗速度为，且介于［ρ，λ0］之间，要慢于完全无承诺能力情况下的速度λ0，快于完全承诺能力下的速度ρ，初始资源消耗的选择为C0=λTS0，介于完全承诺能力情况与完全无承诺能力情况之间。而且，如果社会计划者(国家)有更强的承诺能力(即T的值越高)，则可耗竭资源的消耗速度越低，选择的初始资源消耗就越低，越能达到资源保护的效果。

同理上述的完全无承诺情形，当模型对任意的ν都有 (ν)=0时，此时又回到了时间偏好不变的跨期消费模型，(5) 式可写为=ρ，从而可知在不变时间偏好情况下，国家在部分承诺能力下的资源最优消耗速度仍为ρ，与承诺能力大小无关。

当Τ趋向于无穷大时，则代表国家具有完全承诺能力。根据笔者对此问题所做的数值模拟，当承诺能力Τ=5时，与完全承诺能力情况下的结果基本接近，从而为规划一般为5年提供了科学的理论根据(有兴趣的读者也可尝试通过设定具体的满足上述假设的 (ν))来对本模型进行模拟)。模拟的结果进一步告诉我们，由于承诺约束了对承诺期T的资源消耗，从而给承诺期的经济主体造成了福利上的损失，因此须对承诺进行一定的补偿。我们可以通过数值模拟来得出不同承诺能力下所应该得到的补偿值。就如何补偿问题，笔者认为，可以借鉴代际迭代模型(OLG)中的思想，以达到动态有效的结果。

3 不足之处与进一步的研究方向

综上所述，在考虑可耗竭资源在代际之间公平分配以维持社会可持续发展的背景下，采用了更符合现实情况的双曲线贴现的可变时间偏好范式，讨论了可耗竭资源的最优消耗问题。模型结果得出，由于社会计划者的行为偏差(短期缺乏耐心与短视行为等)，如果不对其资源消耗行为进行承诺，则会导致可耗竭资源的过度消耗。由于资源的最优消耗速度依赖于承诺能力，而承诺能力的提高会导致更低的有效时间偏好率(贴现率)，因此将导致更低的资源消耗速度和更少的初始资源消耗。因此，承诺技术能纠正社会计划者(国家)的不耐心程度与短视行为，从而达到保护可耗竭资源的目的。

但是，笔者为简单起见，简化了模型的很多因素，譬如，没有考虑人口增长，假定效用函数为对数效用函数，当然这只是为了求出更简洁的显式解，如果假定效用函数为一般的CRRA效用函数，不影响模型命题的性质，当然结果会更复杂一点。另外，模型只单纯讨论了固定存量下的“吃蛋糕”问题。虽然模型对可耗竭资源的保护有一定的政策指导意义，但由于模型没有考虑产品生产下的可耗竭资源的消耗，因而模型设置仍与现实经济情况相差较远。

今后可考虑更为现实的问题是，由于以前在对生产函数的一般讨论中，通常隐含的一个假设是所有的投入不可耗尽。但是很多投入(例如石油和矿产)都是最终可耗尽的。因此，资源最终枯竭的前景必须被考虑进去，因而需要社会计划者在消费品的生产和资源的消耗之间进行权衡(tradeoff)，以便满足社会可持续发展前提下的效用最大化目标。在这种情况下，需要添加一个资本积累演化的约束方程，但仍可按照前面的思路重新求解不同承诺能力下资源与消费品的最优消费路径，分析不同承诺能力对最优消费路径的影响。

自Laibson提出规范的拟双曲线贴现模型以来，可变时间偏好理论已经取得了长足的进展。本文通过运用Barro可变时间偏好的双曲线贴现模型，对国家的资源保护规划(承诺)做出了较为完全的经济学解释，用数理模型证明了政府新近出台的这些保护可耗竭资源的政策的科学性。此外，本文通过一个可耗竭资源的最优消耗的问题，对可变时间偏好的双曲线贴现模型进行了详细的分析，希望能引起读者对承诺在可变时间偏好框架下建模的重视。

References)

［1］Dasgupta P， HealG.TheOptimalDepletion ofExhaustible Resources［J］.The Review of Economic Studies，1974，(41).

［2］Heal G.Optimal Use of Exhaustible Resources［M］.Handbook of Natural Resource and Energy Economics，1993:855 － 880.

［3］Barro R J.Ramsey Meets Laibson in the Neoclassical Growth Model［J］.Quarterly Journal of Economics，1999:1125 － 1152.

［4］Hotelling，H.The Economics of Exhaustible Resources［J］.The Journal of Political Economy，1931，39(2):137 －175.

［5］Stiglitz，J E.Monopoly and the Rate of Extraction of Exhaustible Resources［J］.The American Economic Review，1976，66(4):655－661.

［6］Ramsey，F P.A Mathematical Theory of Saving［J］.The Economic Journal，1928，38(152):543 － 559.

［7］Samuelson，P A.A Note on Measurement of Utility［J］.Review of Economic Studies，1937，(4):151 －161.

［8］Bauer M ，Chytilova J，Morduch J.Behaviorval Foundations of Microcredit:Experimentaland SurveyEvidencefrom Rural India［M］.New York:Finanacial Access Initiative Research Paper，2008.

［9］Jones B，Rachlin H，Delay.Probability and Social Discounting in a Public Good’s Game［J］.Journal of the Experimental Analysis of Bahavior，2009，91(1):61 － 73.

［10］Laibson D.Golden Eggs and Hyperbolic Discounting［J］.Quarterly Journal of Economics，1997，12(2):443 － 77.

［11］Ashraf N，Karlan D ，Yin W.Trying Odysseus to the Mast:Evidence from a Commitment Savings Product in the Philippines［J］.The Quarterly Journal of Economics，2006，121(2):635－672.

The Optimal Depletion of Exhaustible Resources Under Different Commitment

ZHOU WeiWU Kang-ping
(School of Economics and Management，Tsinghua University，Beijing 100084，China)

There is yet no literature focusing on the issue of the optimal dephetion of exhaustible resources in the fromework of variable time preference.This paper attempts to analyze pure consumption of exhaustible resources under hyperbolic time preference，and to discuss the optimal depletion rate and the effect of the protection of exhaustible resources under different commitment abilities.The results of the model show that the case of the hyperbolic discount with the full commitment of the country is equivalent to the case of constant discount of the social planner problem.In this case，the optimal depletion rate and the initial consumption of exhaustible resources are the slowest.On the contrary，they are the highest and the near-sighted behaviors inevitably lead to excessive consumption of exhaustible resources without commitment.Besides，in the case of partial commitment，the results are between the cases of full commitment and those of no commitment.Therefore，with the hyperbolic time preference，the optimal depletion rate of resources depends on the commitment ability.Higher commitment ability leads to lower effective rate of time preference，and consequently，lower depletion rate and lower initial depletion value.The improvement of commitment ability can decrease men’s impatience and nearsighted behaviors，and contribute to the protection of exhaustible resources.

exhaustible resources;time preference;hyperbolic discounting;commitment ability

F061.1

A

1002－2104(2011)05－0021－05

10.3969/j.issn.1002－2104.2011.05.004

2011－02－26

周伟，博士生，主要研究方向为资源与环境经济学。

*高等学校博士学科点专项科研基金资助。

(编辑:李 琪)