滑坡监测的自适应约束抗差滤波算法研究*

左廷英 吴芸芸 宋迎春

(中南大学信息物理工程学院，长沙 410083)

滑坡监测的自适应约束抗差滤波算法研究*

左廷英 吴芸芸 宋迎春

(中南大学信息物理工程学院，长沙 410083)

在滑坡的动态监测中通常存在先验几何信息和物理信息，现有的滤波算法并不能够充分利用这些信息，为控制几何观测异常对形变参数估计的影响，提出一种利用滑坡力学状态信息的约束滤波模型。同时，利用约束方程获得有益信息，精确地确定测量的等价权，给出相应的自适应约束抗差滤波算法，并通过实例说明了带有约束的滤波算法更能提高状态参数估计的可靠性。

约束信息;变形监测;抗差滤波;约束滤波;自适应滤波

1 引言

边坡岩体由初始变形发展到破坏性滑坡，是一个极其复杂的发展演变过程［1，2］，国内外学者已建立了许多动态的滑坡预测预报模型［3-8］。然而，由于影响滑坡的因素非常复杂，而人们的认识又十分有限，因此，滑坡动态分析的难度通常很大，建立的模型常常包含一定程度的误差，从而导致不精确的形变分析结果。在变形观测中，大地测量方面的学者只关注几何观测数据，对形变的物理背景知识了解甚少，当在观测过程出现了异常数据容易造成计算结果的偏差。所以，在建立边坡滤波模型计算边坡形变时，一种合理的方法是将物理力学模型与几何观测模型相结合。Schwintzer［9］于1982年提出了这种建模思想，Bock等［10，11］对这一建模思想进行了进一步的拓展，他们根据地球物理模型和实测几何数据建立变形监测模型，应用抗差估计理论来调整先验信息对计算结果的影响。Segall和Matthews［12］建立了一个几何观测位移量和物理模型预测位移量间的差异达到最小的原则，用来解算变形体的形变量。为了精确地跟踪滑坡的动态变化，我们提出一种新的方法，即把边坡的几何约束信息、力学状态结合起来，建立一个混合的滤波模型，合理地利用先验的几何信息和物理信息建立关于状态参数的约束方程，再利用这些约束信息来控制几何观测异常对形变参数估计的影响。

2 滑坡的滤波模型

依据滑动面的类型不同，滑坡类型可分为平面型、契型、曲面型和倾倒型等多种形式［13］。若把滑坡视为一个平面问题，那么可以用一个块体系统来描述(图1)［14］。为了让问题变得简单，假设块体为刚体，并且块体的几何形状和力学性质都是预先知道的，由牛顿第二定律可知块体系统中的任何一块的运动方程可表示为(图2)。

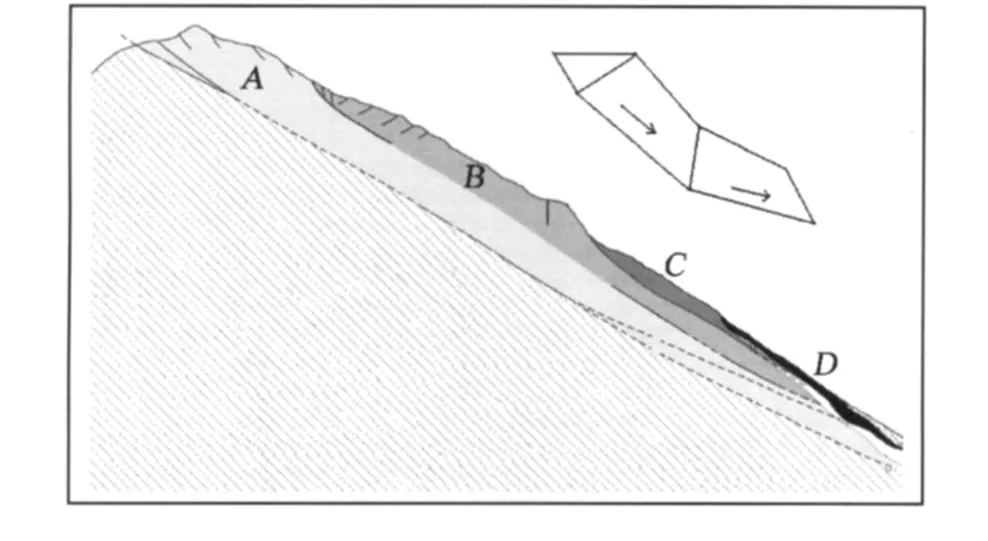
图1 块体系统Fig.1 Block system

图2 刚体受力状态示意图Fig.2 Geometry and forces associated with a rigid block

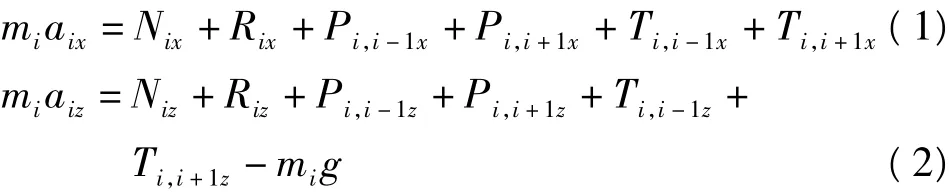
式中，aix、aiz表示第i块滑块的加速度，N表示滑块的正压力，R表示滑块所受的摩擦阻力，Nx、Nz、Rx、Rz为N和R中的在x和z方向受力的分量，m为块体的质量，g为重力加速度，P和T是相邻块对它的作用力，xi、zi是块体的位移量。

方程(1)、(2)也可表示为

这里

对于整个块体系统，由式(3)可构成

这里，M和A1由Mi和A1i组成，

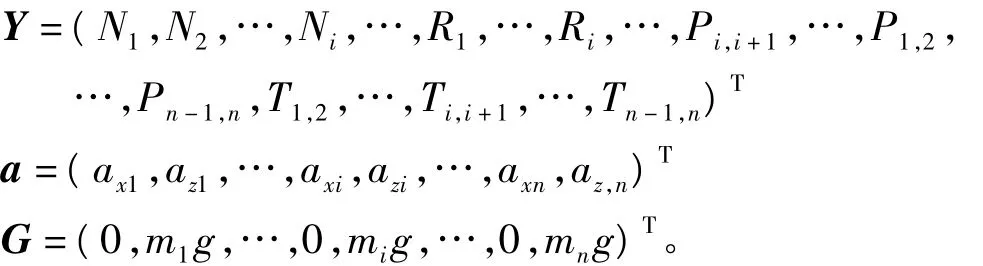
方程(3)表示的是一个刚体系统的运动方程，如果系统中只有一个块体，必有：

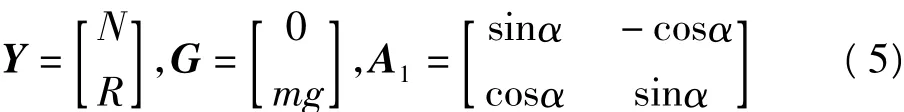
假设块体为刚体，并且各块体面保持相互接触，这时滑体将沿滑动面向下运动，在滑动面的法方向上的运动显然为0，即

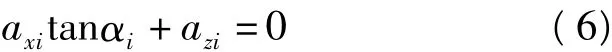
如果系统中有n块滑体，则必有n个类似式(6)的方程。

此外，由于各块体面之间保持相互接触，相邻块体的位移、速度和加速度在垂直于接触面的法线方向上都是相同的，即对于加速度有：

如果有n个滑动块体，则必有n-1个类似式(7)的方程。对整个滑体系统，方程(6)、(7)可以组合成：

A2按(6)、(7)组成。

摩擦力为：

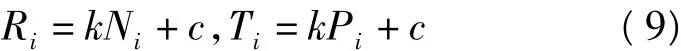
其中，k表示摩擦系数，c表示内聚力，对n个块体的块体系统，就有2n-1个类似式(9)的方程。所有这些方程写成

为了方便计算，我们对参数Y进行如下变换，即让Y=Y0+ΔY，这里Y0是Y在滑体处于极限平衡状况下的取值。因为，在极限平衡状态下，任意块体的加速度值应该为0，所以有axi=azi，由式(4)可得：

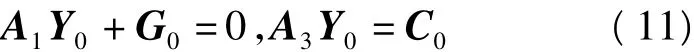
式中，G0、C0是G在极限平衡状态下的取值。由式(4)、(8)和(11)可得：

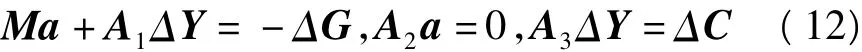
这里，ΔY=Y-Y0，ΔG=G-G0=(0，Δm1g，…，0，Δmig，…)，显然ΔY是表示滑体当前状态与稳定状态之间的差别。

X1是位移向量，V=是速度向量，滑体的状态可用X=(，，aT，ΔYT)T状态向量来描述。其中，X1=(x1，z1，…，xi，zi，…)T，V==(vx1，vz1，…，vxi，vzi，…)T，a==(ax1，az1，…，axi，azi，…)T。

按照刚体运动方程可以得到，刚体的运动从状态k转移到k+1时，其位移和速度有：

除一些特殊原因外，作用在滑体上的外力通常没有大的变化。因此，可以假定ΔG=0及ΔYk+1= ΔYk。当外力发生微小变化时，则可以把它们看成中状态转移误差(系统噪声)。因此，由方程(12)可得：

由式(13)和(14)可得状态转移方程为

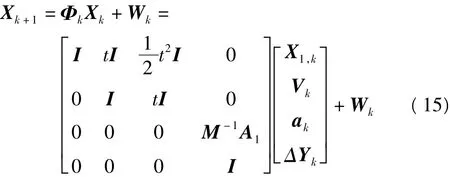
在边坡监测中观测方程可表示为

这里，Hk=(I 0)，Lk表示观测向量，ek表示观测误差。

在刚体假设下我们可以建立某些约束条件，例如由式(12)，有：

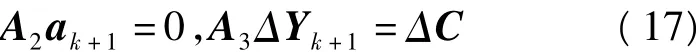
式(17)可以用作为几何约束。此外，相邻两块体的位移和速度接触面的法向上应该相同，因此，类似于式(10)，有：

式(17)和(18)可合并为DkXk=dk，这里

由式(15)～(17)得到的变形监测的滤波模型为：

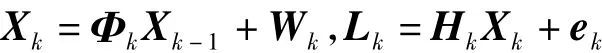
其中，Xk为tk时刻的状态向量，Φk为状态转移矩阵，Wk为动态噪声向量。式中Lk为观测向量，Hk为设计矩阵，ek为观测噪声向量，ek和Wk不相关。

3 自适应约束滤波算法

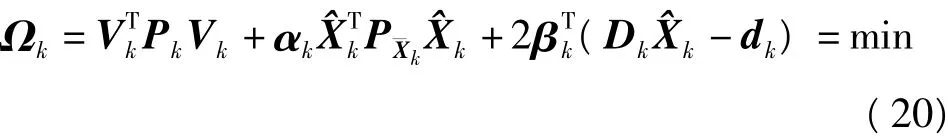
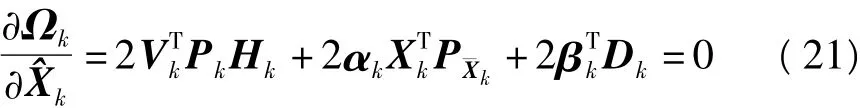
考虑测量误差方程Vk=Hk-Lk，则带约束的状态估计为［17］：

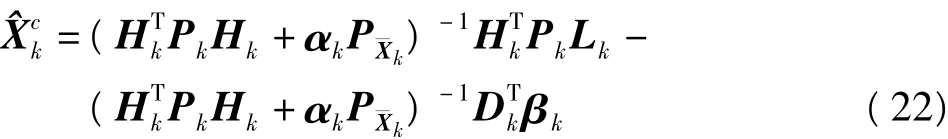
容易发现，式(22)的第一项与自适应卡尔曼滤波估计类似。设

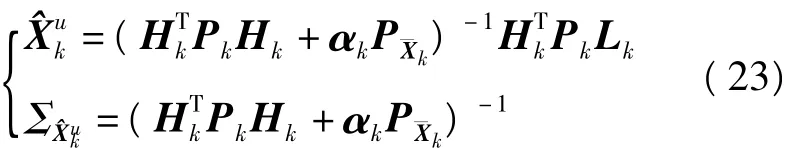
估计式(25)几乎和带等式约束的标准卡尔曼滤波递推公式相同，自适应因子通过一步向前估计式(23)影响状态估计，假若和被看成是先验信息，那么自适应等式约束卡尔曼滤波是非常类似标准卡尔曼滤波。

4 自适应因子的确定

4.1 状态不符值统计量

一个统一的自适应因子能够方便地调节测量信息对预测状态估计的贡献，简化实时处理的计算。文献［18］给出的由状态不符值所构建的自适应因子为：

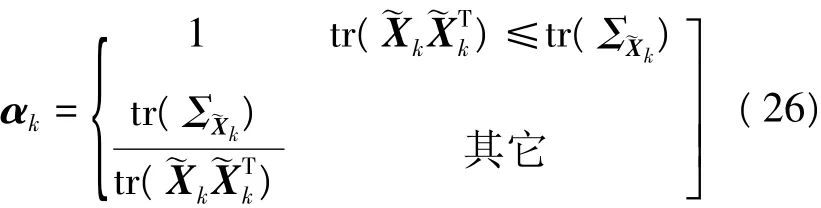
4.2 预测残差统计量

当tk历元观测信息Lk可靠时，其相应的预测残差=Hk-Lk，预测残差的理论协方差阵为=HkHk+Σk。反映了动力学模型的误差大小，利用它可以构造自适应因子［18］：

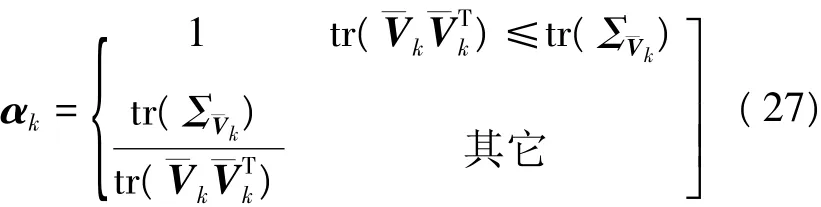
5 实例解算与分析

以湖南某高速公路边坡监测为例，该边坡已采用抗滑桩进行处治，边坡重量大约10吨，实测α1= 45°。在抗滑桩上布设观测点，观测三维位移。采用两台GPS接收机连续静态模式观测，采样率为15 s，基线每3小时计算一次结果，共观测了6个月。由于观测期间有一台GPS接收机信号缺失，无法获得正常GPS观测值，导致某些时间段的观测数据出现了一些异常，因此位移的计算结果脱离实际，本例将通过先验约束信息对其中一个边坡观测数据进行校正，滤波结果与正常接收机的计算进行比较。设计了3种计算方案：

方案1：采用常见的卡尔曼滤波计算。

方案2：采用无约束的自适应抗差滤波式(23)计算，自适应因子按照式(26)计算。

方案3：采用约束自适应抗差滤波式(25)计算，自适应因子按照式(26)计算。

图3～5给出了3种方案的计算结果(每个历元的结果是按照3小时的静态计算为一个结果)，从分析计算结果可以看出：

1)由于接收机信号缺失导致观测误差异常，利用方案1的标准卡尔曼滤波进行状态参数估计求得的形变位移参数，与用正常观测数据求得的形变位移参数相比较，存在较明显的偏差(图3)，特别是在历元800～1 000附近出现了较大的抖动，这说明用标准的卡尔曼滤波算法不能有效地校正因观测异常导致的滤波结果的偏差。

2)方案2中，因为采用了无约束的自适应抗差滤波，其形变参数的计算精度均有很大的改善(表1)，说明自适应因子起到了调控作用，它能很好地平衡物理力学信息和观测信息对形变参数估计的贡献，然而由于观测本身并不可靠，要完全修正观测结果是比较困难的。从图5可见，对于历元800～1000附近出现的抖动仍然无法修复。

表13 个方向的RMS表(单位：mm)Tab.1 RMS of three components(unit：mm)

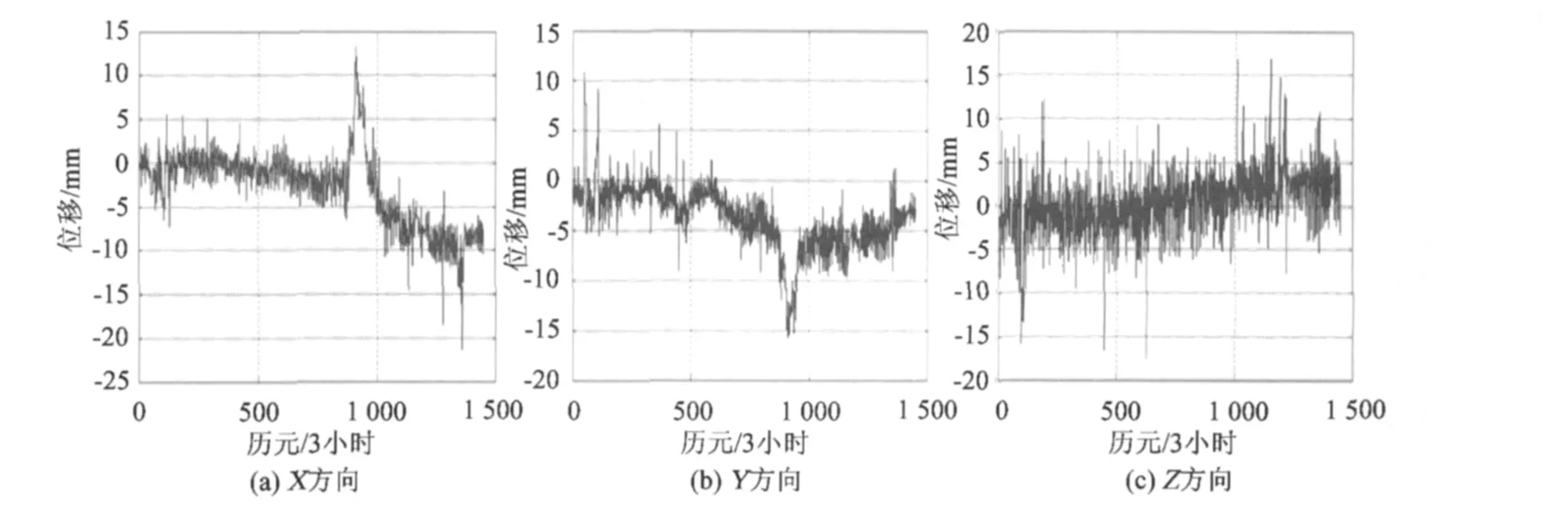
图3 方案1的X、Y、Z方向误差曲线图Fig.3 Displacement curves in X，Y，Z of Scheme 1

3)方案3中，由于增加了约束信息，当观测不足情况下，起到了补充观测信息的作用，因此，能够修补因为长时间观测异常引起的结果偏差(图5)，说明用带有状态约束的抗差自适应滤波算法可以有效地校正因观测异常导致滤波结果的偏差。

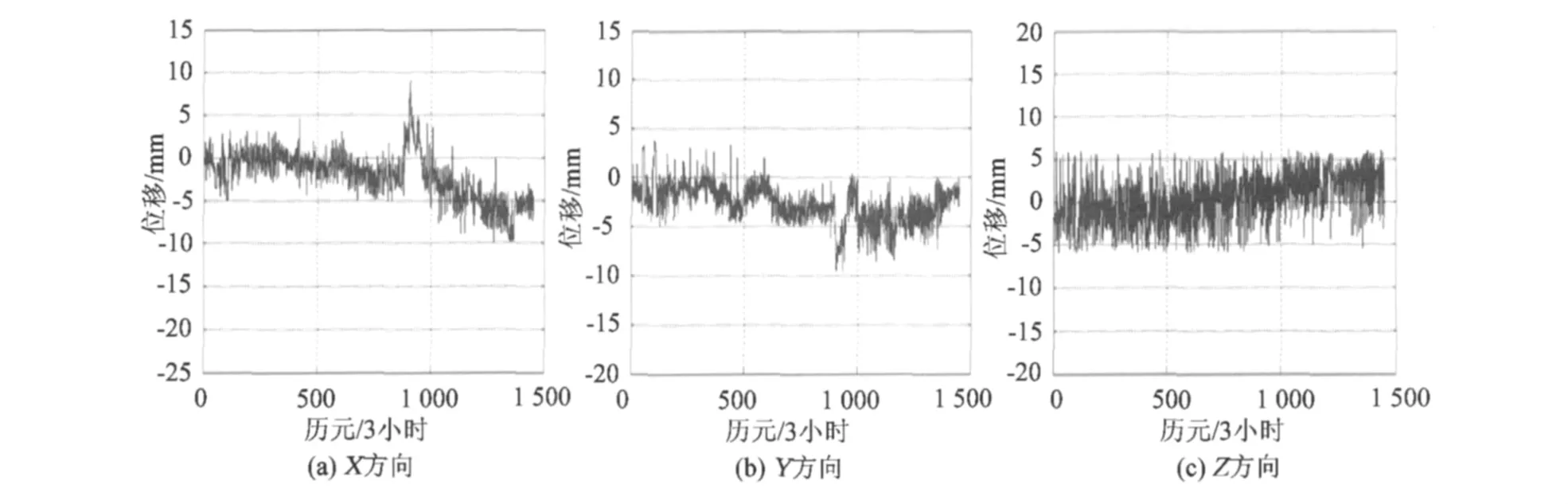
图4 方案2的X、Y、Z方向位移曲线图Fig.4 Displacement curves in X，Y，Z of Scheme 2

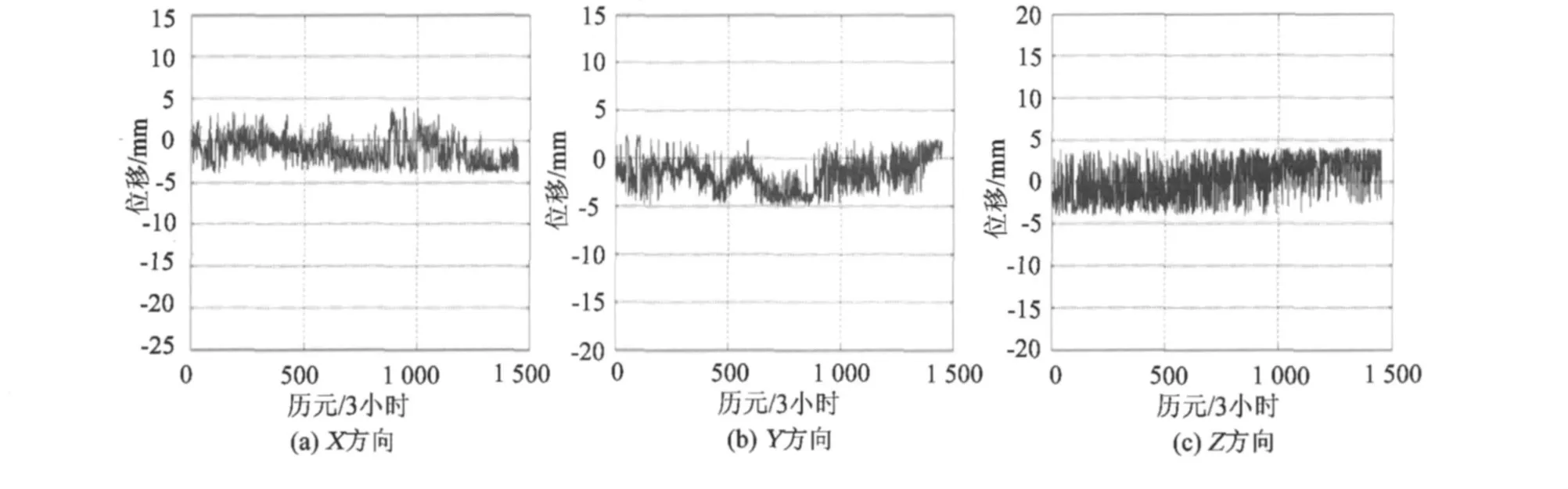
图5 方案3的X、Y、Z方向位移曲线图Fig.5 Displacement curves in X，Y，Z of Scheme 3

6 小结

模型的不确定性或模型误差会严重影响滤波的分析结果，甚至会导致滤波的发散。本文采用附加先验约束信息来消除或削弱模型误差的影响。先验约束信息常存在于边坡的动态监测模型中，但是现有的滤波算法并不能够充分利用这一信息，针对这一点，提出了一种状态变量带有约束的抗差滤波算法，由于约束信息能够改善量测残差，使得滤波解算过程可以从约束方程中获得有益信息，因此，带有状态约束的抗差滤波算法能够改善状态估计的精度。可靠的残差可以导致精确地确定测量的等价权，因而可以改善滤波解的可靠性。约束滤波递推解与无约束的卡尔曼滤波递推解非常类似，无约束的状态估计可以用来评价状态估计，然后约束方程再来对状态估计进行更新。在抗差估计中，无约束滤波过程首先提供一个初始的状态估计解，然而再综合利用约束信息进行更新。实例解算说明，抗差自适应滤波和带约束的抗差自适应滤波都能够改善状态参数的精度。然而，考虑边坡的几何约束信息、力学状态，将变形监测数据通过卡尔曼滤波就可以结合起来，更能够加强滤波解算结果的可靠性，有效消除或削弱模型误差的影响。

1 Zangerl C，Eberhardt E and Perzlmaier S.Kinematic behaviour and velocity characteristics of a complex deep-seated crystalline rockslide system in relation to its interaction with a dam reservoir［J］.Engineering Geology 2010，112：53 -67.

2 Bonzanigo L，Eberhardt E and Loew S.Long-term investigation of a deep-seated creeping landslide in crystalline rockgeological and hydromechanical factors controlling the Campo Vallemaggia landslide［J］.Canadian Geotechnical Journal，2007，44(10)：1 157-1 180.

3 朱建军，丁晓利，陈永奇.集成地质、力学信息和监测数据的滑坡动态模型［J］.测绘学报，2003，32(3)：261-266.(Zhu Jianjun，Ding Xiaoli and Chen Yongqi.Dynamic landsliding model with integration of monitoring information and mechanic information［J］.Acta Geodaetica et Cartographica Sinca，2003，32(3)：261-266)

4 Yang Yuanxi and Zeng Anmin.Adaptive filtering for deformation parameter estimation in consideration of geometrical models［J］.Science in China Series D：Earth Science，2009，52(8)：1 216-1 222.

5 Shi G H.Block system modeling by discontinuous deformation analysis［M］.Computational Mechanics Publications，Southampton UK and Boston USA，1993.

6 Bonaldi D.Displacement forecasting for concrete dams via deterministic mathematical models［J］.Water Power＆Dam Construction，1977，29(9)：74-78.

7 Purer E.Application of statistical methods in monitoring dam behavior［J］.Water Power＆Dam Construction，1986，38 (12)：16-19.

8 DeSortis A，Paoliani P.Statistical analysis and structural identification in concrete dam monitoring［J］.Engineering Structures，2007，29：110-120.

9 Schwintzer P.Generalization for deformation vector with hybrid model［A］.In：I JoÓ，A.Detreköi，eds.Deformation Measurements［C］.Budapest：Akademiai kiadó，1982：453 -463

10 Bock Y.Estimating crustal deformations from a combination of baseline measurements and geophysical models［J］.Bull Geod.，1983，57：294-311.

11 Bock Y，Schaffrin B.Robust predication of the Earth’s crustal movements from precise geodetic data and a vague geophysical mode［R］.The first World Congress of BernoulliSociety on MathematicalStatistics. Taschkent (USSR)，1986.

12 Segall P and Matthews M V.Displacement calculations from geodetic data and the testing of geophysical deformation model［J］.J Geophys Res.，1988，93(B12)：14 954-14 966.

14 Lü W C and Xu S Q.Kalman filtering algorithm research for the deformation information series of the similar single difference model［J］.Journal of China University of Mining and Technology，2004，14(2)：189-194.

15 Hoek E and Bray J W.Rock slope engineering［R］.The Institution of Mining and Metallurgy，London，1981.

16 Ren D and Ding X.Dynamic deformation analysis of open pit slopes［R］.The 8th Fig International Symposium on Deformation Measurements，25-28 June 1996，Hongkong：157-163.

17 Yang Y，He H and Xu G.Adaptively robust filtering for kinematic geodetic positioning［J］.Journal of Geodesy，2001，75(2/3)：109-116.

18 Yang Y，Gao W and Zhang X.Robust Kalman filtering with constraints：a case study for integrated navigation［J］.Journal of Geodesy，2010，84：373-381.

19 Yang Y and Gao W.An optimal adaptive Kalman filter［J］.Journal of Geodesy，2006，80： 177-183.

ADAPTIVELY ROBUSTLY CONSTRAINED FILTERING ALGORITHM FOR SLOPE MONITORING

Zuo Tingying，Wu Yunyun and Song Yingchun
(School of Info.Physics and Geomatics Engineering，Central South University，Changsha 410083)

For the rational use of geometric and physical information of slope，and in order to control the influence of outliers on deformation parameter estimation，a constrained filtering model using mechanical state information of slope is given.At the same time，the algorithm utilizes the useful information in constrained equation to accurately determine the equivalent weights of measurements，thus the relevant adaptive robust constrained filtering algorithm is given.By a pratical example，it is proved that this algorithm can improve the reliability of state parameter estimation.

constrained information;deformation monitoring;robust filtering;constrained filtering;adaptive filtering

1671-5942(2011)06-0094-06

2011-04-23

国家自然科学基金(40874005);教育部博士点基金(200805331086)

左廷英，女，1964年生，副教授，研究方向：测量数据处理.E-mail：zty2003@163.com

P207

A