一个非局部抛物方程的稳态解及其稳定性

2011-11-13尹洪辉

淮阴师范学院学报（自然科学版） 2011年2期

关键词：抛物稳态安徽

梁飞, 尹洪辉

(1.安徽科技学院理学院, 安徽凤阳 233100； 2.淮阴师范学院数学科学学院, 江苏淮安 223300)

一个非局部抛物方程的稳态解及其稳定性

梁飞1, 尹洪辉2

(1.安徽科技学院理学院, 安徽凤阳 233100； 2.淮阴师范学院数学科学学院, 江苏淮安 223300)

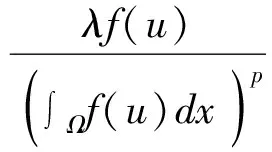
非局部抛物型方程; 稳态解; 整体存在

0 引言

在本文中, 我们主要考虑下述非局部抛物方程的稳态解及其稳定性:

(1)

这里λgt;0, 0lt;p≤1,f满足条件

(2)

一个相似的问题

(4)

吸引了研究者的兴趣[1-4].Antontsev和Chipot[5]利用能量方法证明了方程(4)解的爆破性,并在文[6]中把结果进一步提高.Lacey[7,8]和Tzanetis[9]分别研究了方程(4)对应于一维和二维径向对称解的渐近性态,首次利用稳态解的方法求出爆破的临界值λ*,并利用稳态解构造出一个随时间递增的下解证明出当λgt;λ*时方程(2)的解是爆破的.另外,如果f是增函数,方程(2)的解不可能发生爆破[7,10].

1 稳态解

我们首先考虑问题(1)的稳态问题,对应于(1)的稳态问题是

(4)

为了研究非局部稳态问题(4),考虑下述椭圆方程

Δw+μf(w)=0,x∈Ω;w=0,x∈∂Ω

(5)

为了建立非局部问题(4)和局部问题(5)之间的关系,对于任意μ≥0的,令

(6)

因为w(x;μ)是非负的,所以这样定义的函数是有意义的.由于w(x;μ)对μ是解析的,不难推断函数λ(μ)对μ也是解析的.下面的定理建立了非局部问题(4)和局部问题(5)解之间的关系.证明是显然的.

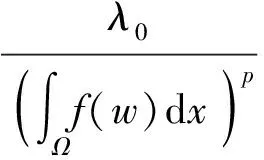
上述定理允许我们通过分析函数λ(μ)的性质来研究问题(4).下面的引理给出(5)解的一些性质.

引理2 设w(x;μ)是问题(5)的解,则有

(i)w(x;μ)关于μ是严格递增的,并且对于固定的μ,wμ在Ω内是有界的.

证明方程(5)对μ求导,得到

(7)

下面利用引理2证明对于0lt;p≤1问题(4)的解是唯一的.

定理3 如果0lt;p≤1,则对于任意的λ≥0,问题(4)的解是唯一的.

证明由定理1, 只需证明λ(μ)是严格递增的.对方程(4)在Ω上积分,我们有

(8)

对μ求导得

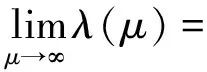
证毕.

2 稳定性

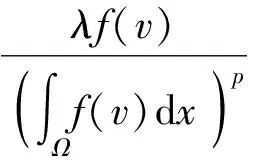
让μ(t)是下面方程

(9)

的解.如果存在μ0使得

λ≤λ(μ0),w(x;μ0)≤u0(x),

则μ(t)递减的.从而v(x;t)也是递减的并且满足

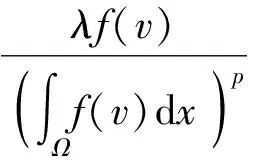
所以v(x;t)是(1)的一个递减的上解.如果存在μ0使得

λ≥λ(μ0),w(x;μ0)≤u0(x),

则μ(t)递增的.从而v(x;t)也是递增的并且满足

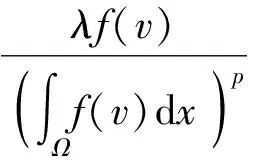
所以v(x;t)是(1)的一个递增的下解.

有了以上的准备, 就可以讨论问题(1)解的稳定性.

定理4 设0lt;p≤1,对任意的λgt;0,(1)的解是整体存在的,其稳态解是全局渐近稳定的.

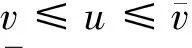
证毕.

[1] Krzywicki A, Nadzieja T. Some results concerning the Poisson-Boltzmann equation?[J].Zastosowania Mat Appl Math, 1991, 21(2): 265-272.

[2] Cimatti G. Remark on existence and uniqueness for the thermistor problem under mixed boundary conditions?[J].Quart J Appl Math, 1989, 47: 117-121.

[3] Kavallaris N I, Tzanetis D E. Blow-up and stability of a non-local diffusion-convection problem arising in Ohmic heating of foods?[J]. Differential Integral Equations, 2002, 15(3): 271-288.

[4] Kavallaris N I, Tzanetis D E.On the blow-up of a non-local parabolic problem?[J], Appl Math Lett, 2006, 21: 921-925.

[5] Antontsev S N, Chipot M. The thermistor problem: existence, smoothness, uniqueness, blow-up?[J].SIAM J Math Analysis, 1994, 21: 1128-1156.

[6] Antontsev S N, Chipot M. The analysis of blow-up for non-local the thermistor problem?[J].Sb Math J, 1997, 38: 827-841.

[7] Lacey A A. Thermal runaway in a nonlocal problem modelling Ohmic heating, Part I: Model derivation and some special cases?[J]. European J App Math, 1995, 6: 127-144.

[8] Lacey A A. Thermal runaway in a nonlocal problem modelling Ohmic heating, Part II: General proof of blow-up and asymptotics of runaway?[J].European J Appl Math, 1995, 6: 201-224.

[9] Tzanetis D E. Blow-up of radially symmetric solutions of nonlocal problem modelling Ohmic heating?[J]. Electron J Diff Eqns, 2002, 11: 1-26.

[10] Bebernes J W, Lacey A A. Global existence and finite-time blow-up for a class of non-local parabolic problem, Part I: Model derivation and some special cases?[J], Adv Differential Equations, 1997, (2): 927-953.

[11] Sattinger D H. Monotone methods in nonlinear elliptic and parabolic boundary value problems?[J]. Indiana Univ Math. J, 1972, 21: 979-1000.

[12] Gilbarg D, Trudinger N S. Elliptic Partial Differential Equations of Second Order?[M].Springer-Verlag Berlin, 1977.

[责任编辑：李春红]

StationarySolutionandStabilityforaNonlocalParabolicEquation

LIANG Fei1, YIN Hong-hui2

(1.School of Science, Anhui Science And Technology University, Fengyang Anhui 233100, China)(2.School of Mathematical Sciences Huaiyin Normal University, Jiangsu Huaian 223300,China)