轧机滚动轴承载荷特性优化及边界元法解析

李 明，吕照宇

(1．燕山大学机械工程学院，河北 秦皇岛 066004;2．邯宝钢铁有限公司热轧厂，河北 邯郸 056015)

0 前言

轧机宽系列滚动轴承是轧机上的关键部件，每年在轧机上消耗大量的滚动轴承。当前日本大型轧机设备事故中，轴承的短寿烧损事故率仅次于轧辊［1］。大多轧机滚动轴承都没有实现其设计寿命，频繁出现如卡死、断裂等各种事故，导致过早磨损、接触疲劳失效等问题［2］。提高滚动轴承寿命，一直是行业内的重要研究课题。

就轴承而言，提高寿命的方法是提高其承载能力。一般来说，有外来影响因素，如安装调整、使用保养、维护修理等;也有内在影响因素，包括轴承设计工艺、制造工艺、材料等。经过多年的研究发展，在优化设计轴承结构、改进轴承加工工艺、提升轴承材料质量、先进的润滑管理和维护等方面已有了很多改进措施。

轧机轴承具有区别于一般轴承的重载特性，因此不仅要从轴承自身承载能力找原因，另一方面，轴承运行时的承载状态更是影响轴承寿命的直接因素［3］。关于这方面的研究，目前的主要成果是静定性辊系设计理论［4］。通过优化设计轴承座提升轴承的使用寿命是近来最新的研究成果。本文采用边界元法解析轴承三维载荷特性，分析了某600四辊轧机轴承座优化设计改善轴承承载状态的影响规律，对延长轧机轴承寿命研究具有普遍意义。

1 轧机轴承三维载荷特性解析的边界元法

轧机滚动轴承由内环、滚动体和外环组成，属多物体接触问题，因此直接分析其负荷特性较复杂而困难。目前，已有许多学者采用数值方法求解轧机滚动轴承负荷特性，有蒙特卡洛法［5］和有限元法［6］。

此外，还有其他学者在三维弹性接触边界元法－面力子单元法的基础上，采用不同形状板单元描述相应形状滚动体，并置于内环上，从而将多物体接触问题简化成两物体接触问题，构建了专用于轧机轴承解析的三维边界元法计算程序［7-8］。该方法具有计算模型直观、简单和较高的计算精度，为设计和分析轧机滚动轴承负荷特性的有效数值方法。

由式(1)～(3)和图1可以看出，滚子在轧机滚动轴承中对接触状态的影响只关系到径向位移，而其余方向位移对接触状态均无影响，当中间滚子用板单元描述时，规定板单元只有径向位移，其余方向均无变形，并将板单元径向位移和以间隙形式代入总体矩阵方程迭代求解，则不会影响计算精度。板单元的径向位移和按Hertz公式进行求解。其总间隙为

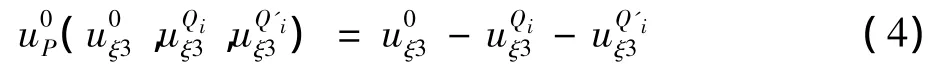
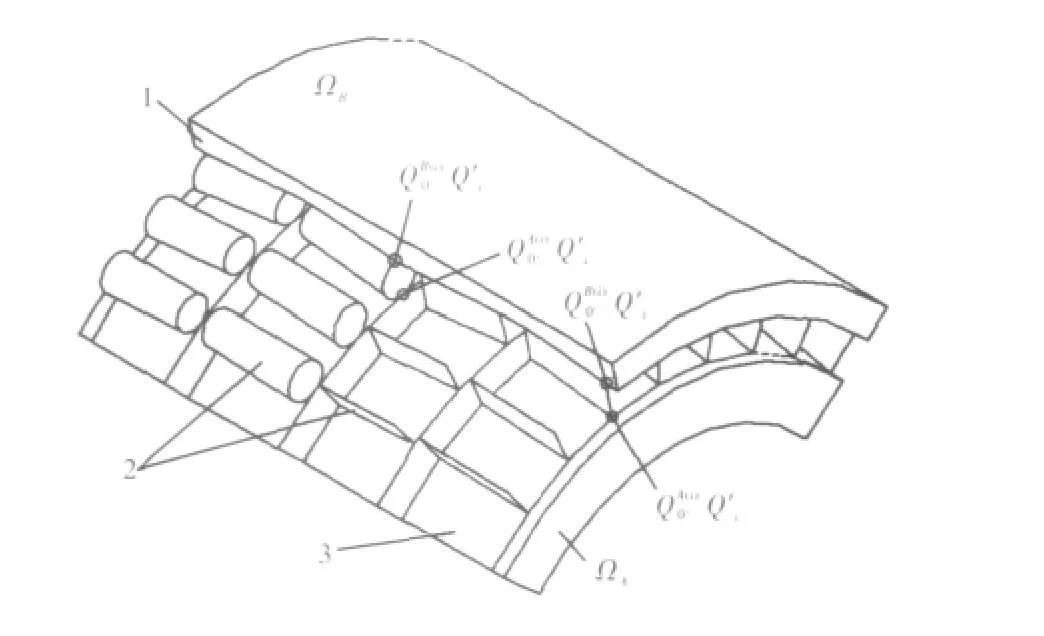
图1 滚动轴承接触状态Fig.1 Contact status of roller bearing

当轧机滚动轴承采用板单元描述后，对子单元分别计算并加以叠加可得到整个单元的面力影响系数。将轧机滚动轴承内外环A、B边界进行离散，板单元固接于内环上，可建立矩阵方程

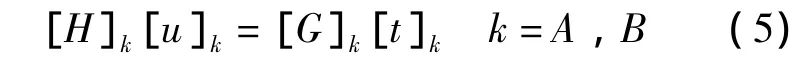
式中，［H］k、［G］k为物体k的位移及面力影响系数矩阵;［u］k、［t］k为物体k的位移及面力列阵。

用轧机轴承解析的三维边界元法计算某600四辊轧机四列滚动轴承载荷三维分布，部分参数见表1。计算模型(支承辊)如图2所示。离散后的模型如图3所示，简化了轴承座上安装止推轴承的部分结构。离散后，轧辊划分698节点，696个四节点线性单元;轴承座划分986节点，986个四节点线性单元;共192对接触点对。

表1 轧机参数Table 1 Parameters of rolling mill

借鉴已有的静定性辊系设计理论［4］，该600四辊轧机设计为静定性辊系，后续的计算结果均以轴承座具有自位性为基础。

2 轴承座双支点承载优化的载荷特性

在延长轧机滚动轴承寿命的研究过程中，计算高刚度轧机［9］和2050CVC 工作辊［10］的轴承载荷发现，轴承座承载方式改变时，轴承的三维载荷分布不再是传统的抛物线型，而是呈现“M”型，且载荷峰值明显降低。基于以上研究成果，在本文提及的600四辊轧机中设计轴承座双支点机构如图4和图5所示。

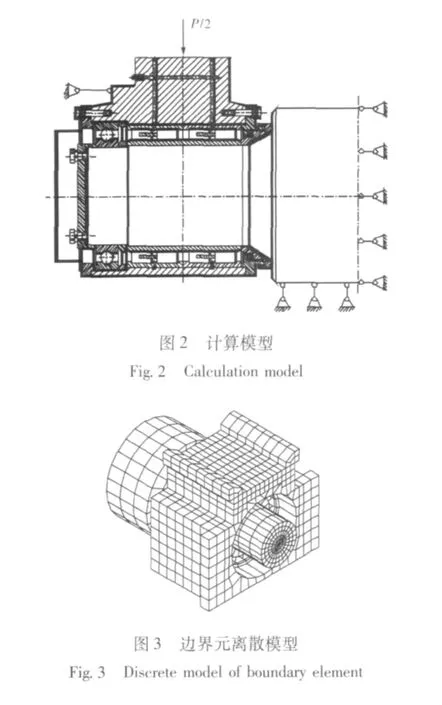
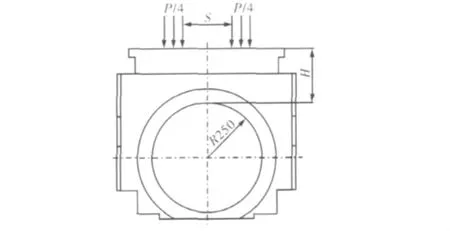
图4 轴承座双支点承载形式Fig.4 Loadcarrying mode of double supporting points of bearing pedestal

轴承座在单支点和双支点两种承载形式下，计算得到四列滚动轴承的三位载荷分布如图6、图7所示。a、b、c、d分别指从靠近辊身侧至远离辊身侧的四列轴承滚子。计算时，图4中分力座支点间距S=240 mm，轴承座镗孔至顶面厚度H=250 mm。

从图6、图7中可以看出，在两种承载形式下，载荷分布规律均遵循作用于最靠近辊身侧轴承滚子上的载荷最大，最远离辊身侧轴承滚子上的载荷最小，但不同承载形式时的极值和承载包角不相同。

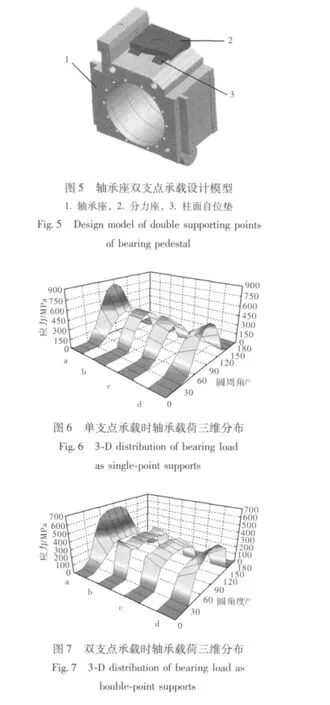
最靠近辊身侧接触点应力曲线如图8所示。单支点承载时，轴承滚子上的载荷峰值为845 MPa;双支点承载时，轴承滚子上的载荷峰值降至649 MPa，相比于单支点承载，载荷峰值降低23.2%(1－649/845=23.2%)。同时，从图8中还可以看到，双支点承载时，轴承滚子承载包角(150°)大于单支点承载时的承载包角(120°)。

两种不同轴承座承载形式时各列轴承滚子的载荷分配如图9所示。

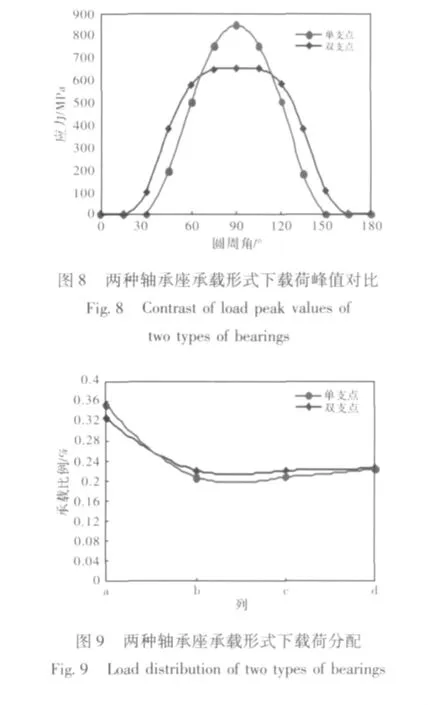
单支点时，承载比例最大的轴承滚子占总载荷的比例为35.3%;双支点时，承载比例最大的轴承滚子占总载荷的比例为32.7%。以理想均布载荷，即总载荷平均分配给四列滚子(每列滚子各承受总载荷的25%)的状态为比较对象，单支点时的最大偏载率为1.412(35.3% ÷25%=1.412)，双支点时的最大偏载率为1.308(32.7%÷25% =1.308)，单支点和双支点承载方式的偏载率相对差仅7.4%，对轴承使用寿命的影响不大。

3 轴承座承载刚度优化的载荷特性

在采用了双支点承载方式后，通过改变图4中的参数H(轴承座受力部位厚度)，改变轴承座刚度，进一步降低轴承载荷峰值。采用边界元法对各个不同H取值的轴承载荷特性进行解析计算，对计算得到的结果中最靠近辊身侧滚动体的接触点应力进行分析，作曲线如图10所示。从图中可以看出，随着轴承座顶部厚度减小，轴承座承载刚度降低，应力曲线由抛物线趋向“M”型，且呈现越来越明显的“M”型形状。而在中间应力逐渐减小的过程中，“M”型曲线的两个尖点逐渐增高。

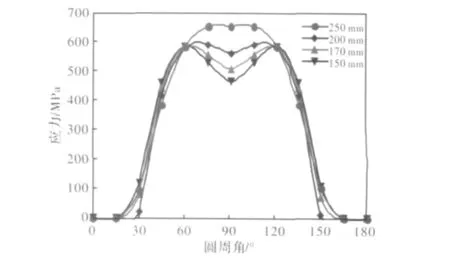
图10 两种轴承座承载形式下载荷峰值对比Fig.10 Contrast of load peak values of two types of bearings pedestal

定义比例ε=H/R，R为轴承座镗孔的半径(250 mm)，以该比例为横轴，以上述计算结果中不同刚度下的载荷峰值为纵轴，得到曲线如图11所示。

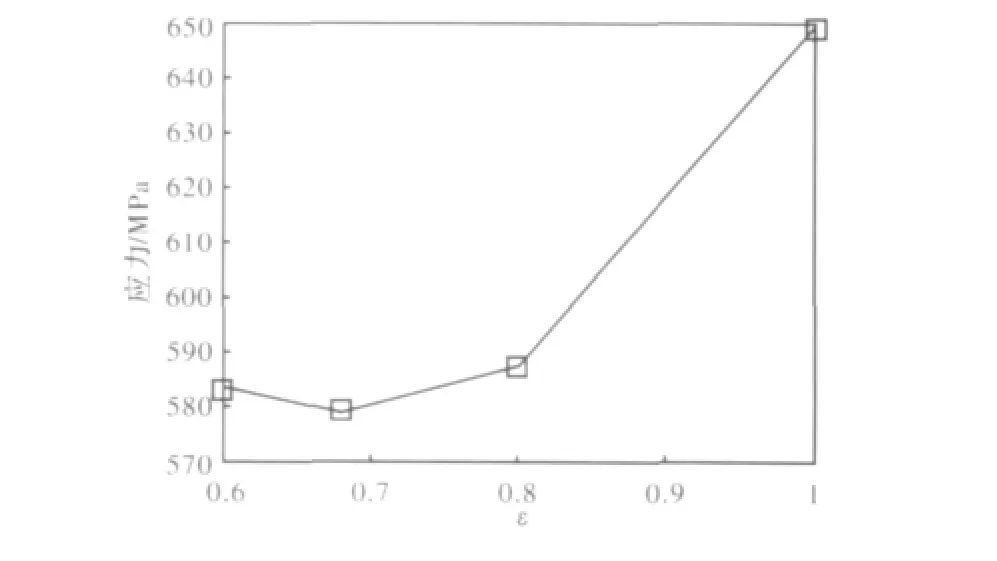
图11 两种轴承座承载形式下载荷峰值对比Fig.11 Contrast of load peak values of two types of bearing pedestal

由图11可知，在一定范围内降低轴承座顶部承载刚度可以降低轴承载荷峰值。图11中，当H从250 mm减小到170 mm时，载荷峰值从649 MPa降至579 MPa，降幅10.8%(1－579/649=10.8%)。

但在承载刚度降低到较小值时，载荷峰值又呈现增加趋势。这是因为承载刚度过低，导致轴承座顶部出现明显弹性变形所致。

4 结论

(1)轧制力通过双支点支座加载在轴承座上，轴承承载状况得到较大幅度改善。对某600四辊轧机的计算结果表明，双支点承载方式时的轴承载荷峰值相比于单支点承载方式降低23.2%。

(2)通过减小轴承座顶部的厚度，优化轴承座承载刚度，也能改善轴承承载状况。对某600四辊轧机的计算结果表明，最优的轴承座顶部厚度为H=200 mm，此时载荷峰值相比优化前降低10.8%，且均载效果良好。

以上措施的实施，大大提高了轴承的使用能力，显著延长了轧机四列滚子轴承(宽系轴承)的使用寿命，对其他轧机轴承座系统的设计具有借鉴意义。

［1］ 瀧本高史，小笠原信夫，法领田宏．21世纪的钢铁生产设备的维修技术［J］．川崎製鐵所技報，2001(1):1－5．

［2］ Harris T A，滚动轴承分析［M］．罗继伟，译．北京:机械工业出版社，1997:129－188．

［3］ 申光宪，安瑞臣，谢朝晖．高刚度轧机重载滚子轴承低寿命问题研究［J］．机械工程学报，1996(2):95－100．

［4］ 申光宪，束学道，李明．轧机微尺度理论和实际［M］．北京:科学出版社，2005．

［5］ 邹家祥．冶金机械的力学行为［M］．北京:科学出版社，1999．

［6］ 周劬惟，孙德志．用三维有限元法分析轧机四列圆锥滚子轴承的负荷分布［J］．重型机械，2000(6):46－48．

［7］ 束学道，申光宪，张连东，等．滚动轴承滚动体板单元模拟的边界元法［J］．重庆建筑大学学报，2000，22(6):50－53．

［8］ Shen Guangxian，Shu Xuedao，Li ming．The 3 － D Boundary element method of roller bearing by plate element analogue［J］．ActaMECHANICA SOLID Sinica，2001，14(3):268 －274．

［9］ 申光宪，束学道，李明等．530空间自位型高刚度轧机［A］．中国钢铁年会论文集(下册)［C］．北京:中国金属学会，2001:235－238．

［10］ 黄庆学，申光宪，陈占福等．宝钢2050 mm轧机组合轴承载荷特性的边界元法解析及试验研究［J］．机械工程学报，2001，37(2):43－47．