热轧地下卷取机牌坊式转向夹送辊设计

2011-11-11张金华

重型机械 2011年6期

关键词：辊的弹塑性牌坊

杨华，张金华

(常州宝菱重工机械有限公司，江苏常州 213019)

0 前言

转向夹送辊是热轧地下卷取机的关键设备，为了便于设计，对牌坊式转向夹送辊的下辊辊径及上辊压下力进行数学建模，并对其进行理论分析。

1 夹送辊的组成及结构

热轧地下卷取机的转向夹送辊由牌坊、上辊、下辊和轴承座及压下油缸，平衡油缸等组成，如图1所示。

为了带钢经转向夹送辊后能向下顺利进入卷取机，牌坊式转向夹送辊结构有以下特征:

(1)在布置上，上辊相对下辊的中心有一向后的偏移距离;

(2)上辊直径大于下辊直径，目的是为了改善咬入条件;

(3)机架为牌坊结构，提高了夹送辊刚性和强度，同时，可以使辊隙和夹紧力设定简单化，另外，可通过C形勾快速换辊。

2 工作原理

当带钢的头部进入夹送辊之前，为了顺利咬入，在位置传感器的控制下，使上辊处于空载辊缝略小于带钢厚度的位置，一般在比板厚小0.4 mm左右［1］。利用上下辊各自的驱动力矩将带钢咬入夹送辊，当钢板进入夹送辊后，压力传感器控制工作侧和驱动侧两个压下油缸，将水平移动的带钢斜向下沿着下辊表面弯曲，使带钢进入地下卷取机，实现转向夹送的目的。另外，当带钢的尾部离开轧机后，利用夹送辊的夹紧力在带钢和夹送辊之间产生的摩擦力形成后张力，从而保证带钢卷紧而不致于塌卷。

图1 夹送辊组成Fig.1 Composite of pressing-sending rolls

3 下辊最大辊径设计

为了保证带钢的顺利弯曲，下辊的辊径越小越好，但是，辊径太小会超出带钢的屈服极限而引起带钢的严重卷曲;又要兼顾减少压力，下辊辊径越大越好，为了使带钢经过转向夹送辊后产生的变形在弹塑性之间，下辊直径要满足一定的要求。根据弹塑性理论可知:

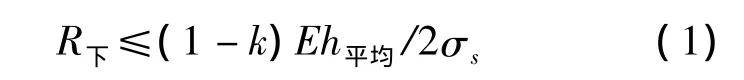
式中，k为弹塑性渗透率，考虑到板的弯曲变形处在弹塑性之间，取k=0.8;h平均为多品种厚度的平均值，一般地下卷取机适应带钢的厚度范围为1.2 ～25 mm［1］，取 h平均=10 mm;σs为带钢的曲服强度，高强度带钢温度在500～700℃时的屈服极限在600 MPa以上，考虑到高强度钢的弹塑性变形，尽量使辊径选小值，故对多钢种带钢的曲服强度取大值，以30CrMnSiA为例，在500℃时，σs=650 MPa［2］，现取 σs=600 MPa;E为材料的弹性模量，在20℃时的弹性模量为E=2.1×105MPa，但由于地下卷取机在夹送辊工位的热轧带钢温度在500～700℃之间［2］，500℃时，钢的弹性模量为0.59 ～1.6 ×105MPa［2］，仍以30CrMnSiA为例，500℃时，E=1.6×105MPa［2］，代入式(1)得:R下≤267 mm，通常下辊辊径的范围为φ400～φ500 mm［2］，现圆整取R下=250 mm。

4 压下力分析

带钢进入转向夹送辊后，受力示意见图2。

图2 夹送辊受力简图Fig.2 Sketch for load carrying force on pinch roll

上辊在压下油缸的作用下将带钢向下弯曲，除了带钢有弹性变形力外，还要将带钢挤压并斜向下输送的夹送力，故在计算压下力时，考虑到平衡油缸的顶出力F2用来克服上夹送辊及轴承座的自重W，把作用在上夹送辊的压下力F1仅分解为克服带钢弯曲所需的压下力F3和带钢挤压产生轧制力N1所需正压力F4。

由于在压下过程中，带钢与夹送辊的接触点不断变化，同时作用在带钢上力的方向不断改变，故给压下力的计算带来困难。为便于计算，将夹送过程假设成轧制和弯曲过程的合成。

4.1 轧制过程按轧制理论计算正压力N1

按轧制理论，正压力N1的计算公式为:

式中，N1为辊缝小于板厚0.4 mm时对带钢的正压力;Q为不同辊径时夹送辊与热轧带钢的接触面积，mm2。

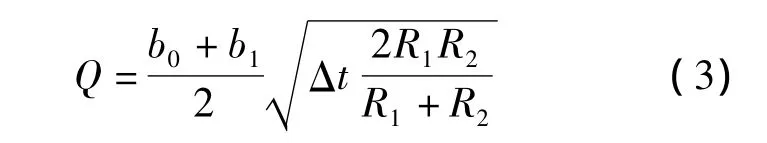
式中，b0为夹送辊之前板宽，按最大板宽计算，取b0=1630 mm;b1为夹送辊之后板宽，取b1≈b0=1630 mm;Δt为热轧带钢的变形量，由于辊缝比板厚小0.4 mm，考虑到牌坊，轴承座和夹送辊的综合变形在0.3以上，带钢的弹性变形，带钢的变形量要小于0.1 mm，现取Δt=0.1 mm;t为板厚，按最大板厚计算，取t=19 mm;R1为下辊半径，R1=250 mm;R2为上辊半径，上辊直径通常在 φ800～ φ950 mm 范围［2］，现取 R2=450 mm。将上述代入式(3)得:Q=9241 mm2。

Pc为热轧带钢对夹送辊的平均单位压力，N/mm－2。

式中，nσ为外抗力系数，查表可得:nσ=1.15［3］;Kε为修正系数，按变形程度曲线得:Kε=0.2［3］。σ30为查曲线数值，要根据 μ 和 ε 求得;ε为变形程度，ε=Δt/t=0.1/19≈0.005=0.5%;μ为变形速度。

式中，v为穿带速度，由于进夹送辊的穿带速度较低，现取v=1.4 m/s;bc为变形区轧件平均宽度，mm，由于变形较小，取 bc=1630 mm，上述代入式(5)得 μ =1.3 s－1。

根据上述数据经查得:碳钢在600℃时，变形程度为 ε =0.3 时，σ30=250 N/mm2［3］，将上述条件代入式(4)、式(2)得:Pc=57.5 MPa，N1=531 kN。

按材料力学公式，将上下夹送辊按两端简支梁建模，经计算可得，当载荷为531kN时，仅上下夹送辊的挠度分别在0.015 mm以上和0.16 mm以上。

4.2 弯曲变形过程中带钢的下压力计算

4.2.1 假设条件

为便于计算，作如下假设

(1)将带钢的弯曲简化成悬臂梁;

(2)将固定点为带钢下表面水平方向和下夹送辊的切点A;

(3)按悬臂梁的长度为e/2时，带钢达到屈服变形时所需的压力值为压下力值。

弯曲带钢的下压力按悬臂梁受力计算，受力如图3所示。

图2中，W为上夹送辊及轴承座重量，由于用平衡缸克服上夹送辊及轴承座的重量，所以W的取值对下压力的计算无关。

F0为上下夹送辊对带钢的挤压力产生的摩擦力，计算公式为:

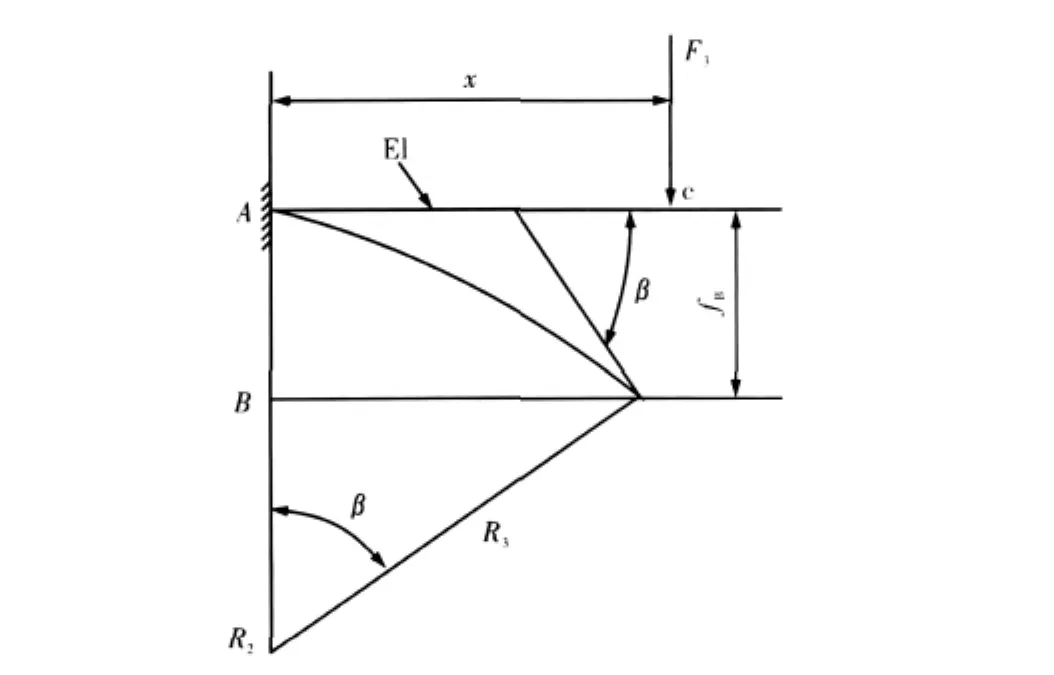
图3 悬臂梁受力Fig.3 Cantilever beam

式中，μ1为夹送辊与带钢之间的摩擦系数;取μ1=0.2。将上述代入式(6)得:F0=102 kN。

为使平衡油缸的顶出力能克服上夹送辊及轴承座重量之和，F2≥W，取F2=W;F3为将钢板弯曲所需的压下力。

设AC之间的距离x为悬臂梁长度，根据《轧钢机械设计》e的取值范围为50～300 mm［3］，现取e=230 mm。

按悬臂梁不同长度，用矫直理论的弹塑性方程求带钢弯曲所需的压下力矩:

将上述代入式(7)得:MS=88264500 N·mm。根据力学中力、力臂与力矩的关系可得:

当x=e=230 mm时，F3=MS/e≈384 kN;当x=e/2=115 mm时，F3=MS/x≈768 kN。当上辊下压到极限时，上辊和带钢的作用点为C，AC为悬臂梁的长度s，根据几何关系可得:sinβ=e/(R1+R2+t)=0.3199，s=R2sinβ≈80 mm。当x=80 mm时，F3=MS/x=1103306 N≈1103 kN。

由此可见，上辊越往下压，带钢的悬臂长度越短，所需的压下力也就越大。

4.2.2 压下力计算

按带钢的轧制力求压下力F4，根据受力情况，从图3中可以看出:F4=N1/cosβ≈561 kN。根据力的叠加关系可列出如下方程