基于模糊层次分析法的选股决策
2011-11-08刘卫锋
何 霞,刘卫锋
(郑州航空工业管理学院 数理系,郑州 450015)
基于模糊层次分析法的选股决策
何 霞,刘卫锋
(郑州航空工业管理学院 数理系,郑州 450015)
针对选购股票的实际情况,应用模糊层次分析法(FAHP)建立了股票选择的数学模型,从而对投资股票项目中的股票优劣进行排序和评价,为选购股票提供一种合理实用的方法。最后通过一个实例对该方法进行了检验,结果表明该方法的实用性和有效性。
模糊层次分析法;股票;选股决策
0 引言
随着我国股票市场的不断发展和完善,股票投资已经成为我国个人投资的主要途径之一。显然,选择什么样的股票作为投资对象是所有股票投资者最关心的问题。但是,股票的选择是一个十分复杂的系统问题,需要同时综合考虑多种因素。于是,针对上述问题,有学者利用层次分析方法(The Analytical Hierarchy Process,简称AHP)[1,2]建立了股票选择的数学模型,为投资者进行股票选择提供了一个参考。但是,层次分析方法本身也存在着一系列缺陷和问题[3],比如,检验判断矩阵是否具有一致性非常困难;当判断矩阵不一致时,可能需要多次进行调整判断矩阵的元素,并进行一致性检验;检验判断矩阵具有一致性的判断标准:CR<0.1缺乏科学依据;判断矩阵的一致性与人类思维的一致性有显著差异;等等。为此,有学者提出了模糊层次分析法[3,4](Fuzzy Analytic Hierarchy Process,简称FAHP),该方法具有反映出人们思维判断的一致性等优点,并且一致性检验和调整简单,从而可以进一步提高决策的可靠性和有效性。
文中利用模糊层次分析法建立股票选择的数学模型,对投资股票项目中的股票优劣进行排序和评价,为投资者进行股票选择提供了一个更加合理实用的方法。最后,文中通过实例验证了该方法的实用性和有效性。
1 模糊层次分析法基本原理
首先,分析影响问题的各个因素,建立递阶层次结构模型。
其次,构造模糊互补判断矩阵。
模糊互补判断矩阵是下层元素针对上层因素的相对重要性两两比较建立的矩阵,其数量标度表示采用如表1 所示的0.1 ~0.9 标度[3]。

表1 0.1 ~0.9数量标度
第三,进行模糊判断矩阵一致性检验及层次单排序。
模糊互补判断矩阵的一致性检验及单层次排序方法[4,5]如下:
求出每个模糊互补判断矩阵A=(aij)nn的排序向量w=(w1,w2,…,wn)T,其中构造出每个模糊互补判断矩阵A=(aij)nn的权重矩阵W=(wij)nn,其中判断矩阵A=(aij)nn的偏差矩阵C=(cij)nn,其中cij=aij-wij。若满意一致性指标0.15,则认为模糊互补判断矩阵是满意一致的。此时模糊互补判断矩阵不需要进行调整,否则需要调整。
第四,进行层次总排序。
在进行了层次单排序及一致性检验后,需要进行层次总排序,这一过程是自上而下地将单准则下的权重进行合成,最终得到的最低层中各元素对于目标的排序权重,即总排序权重。
2 股票选择的模糊层次分析模型
2.1 建立股票选择的递阶层次结构模型
建立股票选择的递阶层次结构模型是利用模糊层次分析法解决选股问题的重点所在。经对股票多方面因素的分析[2],递阶层次结构模型主要分为三层:第一层,最高层为目标层,记为A,即选购股票。第二层,中间层为准则层,记为:B;包括三个准则:主观因素,记为B1;宏观因素,记为B2;客观因素,记为B3。第三层,最低层为子准则层,记为:C;其中,主观因素的子准则包括:期限偏好,记为C11;内部消息,记为C12;风险偏好,记为C13;宏观因素的子准则包括:国家经济,记为C21;大盘走势,记为C22;经济政策,记为C23;突发事件,记为C24;客观因素的子准则包括:股价,记为C31;公司状况,记为C32;股性,记为C33(如图1)。

图1 股票选择的递阶层次
2.2 构造模糊互补判断矩阵
通过两两比较,利用表1中的0.1~0.9标度,建立模糊互补判断矩阵分别为:表2、表3、表4、表5。

表2 模糊互补判断矩阵A-B

表3 模糊互补判断矩阵B1-C

表4 模糊互补判断矩阵B2-C

表5 模糊互补判断矩阵B3-C
2.3 模糊判断矩阵一致性检验及层次单排序
现求出模糊互补判断矩阵A-B的权重向量并对其进行一致性检验:

同理可算出 w2=0.23,w3=0.44,即 A - B 的权重向量为 w=(0.33,0.23,0.44)T。
同理,我们可以得到模糊互补判断矩阵B1-C,B2-C,B3-C的排序向量,权重矩阵及偏差矩阵,并进行一致性检验。在这里,我们只将排序向量及满意一致性指标列出(见表6),权重矩阵和偏差矩阵不再列出。显然,所有的模糊互补判断矩阵都通过了一致性检验。
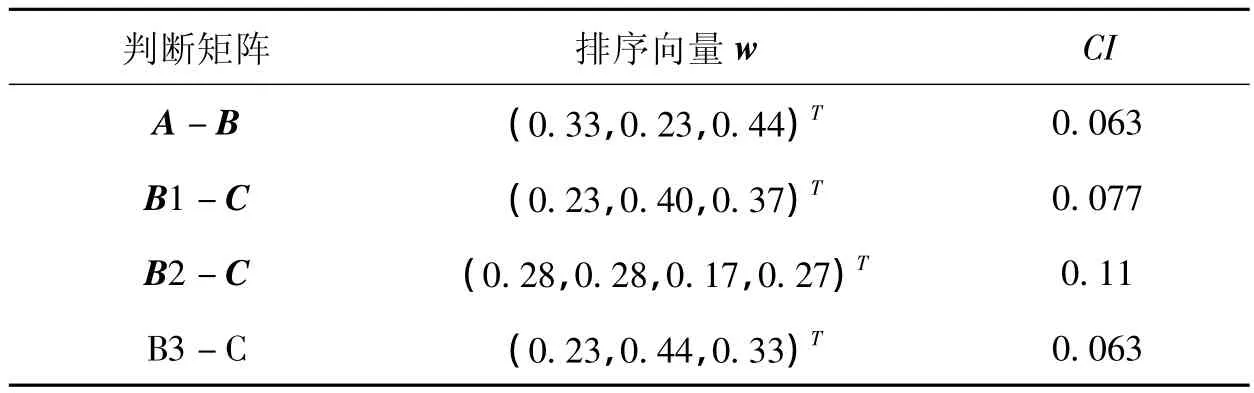
表6 各层次单排序及其一致性检验结果
2.4 层次总排序
在进行了层次单排序及一致性检验后,需要进行层次总排序,这一过程是自上而下地将单准则下的权重进行合成,最终得到的最低层中各元素对于目标的排序权重,即总排序权重(见表7)。
3 应用实例
现选择深圳能源(000027)和上海实达电脑(600734)作为考察的对象,两股票的各因素得分如表8[2]:于是,通过各因素权重分别乘以各因素得分求和,从而得出两只股票的综合得分为:

表7 层次总排序

表8 两股票各因素得分

其中,S1,S2分别是深圳能源和上海实达电脑的综合得分。
显然,若在两只股票中作出决策,购买深圳能源会更好,并且实际也证明了这个结论的正确性[2]。
4 结语
本文建立了股票选择的模糊层次分析模型,克服了层次分析模型的缺点,使得决策更能反映出人们思维判断的一致性,提高决策的可靠性和有效性,从而为投资者进行股票投资决策提供了一个更加有效的工具。
[1] 郭佳.基于AHP的长期投资优良股票选择模型[J].统计与决策,2005(3):11-13.
[2] 高岩,杨国孝.基于层次分析法的选股决策[J].数学的实践与认识,2004,34(10):42-48.
[3] 张吉军.模糊层次分析法(FAHP)[J].模糊系统与数学,2000,14(2):80-88.
[4] 吕跃进.基于模糊一致矩阵的模糊层次分析法的排序[J].模糊系统与数学,2002,16(2):79-85.
[5] 吕跃进.模糊互补判断矩阵的一种一致性调整方法及其收敛性[J].模糊系统与数学,2007,21(3):86-92.
Decision making of stock-selection based on fuzzy analytic hierarchy process
HE Xia,LIU Wei-feng
(Department of Mathematics and Physics,Zhengzhou Institute of Aeronautical Industry Management,Zhengzhou 450015,China)
Considering the actual situation of stock market,this article establishes a mathematical model for making decision on stockselection by using fuzzy analytic hierarchy process(FAHP),and arranges and evaluates the grading of stocks in investment projects,which provides a reasonable method for decision making of stock-selection.Finally,a case study is given to check it,showing that FAHP is a useful and effective method in stock selection.
FAHP;stock;decision making of stock-selection
O223;F224.3
A
1009-3907(2011)06-0043-04
2011-04-26
何霞(1976-),女,河南周口人,讲师,硕士,主要从事应用数学及其教学研究。
责任编辑:钟 声
