串联排队RED/ERED网络分析模型
2011-11-06迟学芬赵莹莹
迟学芬,赵莹莹
(吉林大学 通信工程学院,吉林 长春 130012)
1 引言
业界预测指出,未来的M2M (machine to machine) 连接的网络和终端设备数量远远超过 H2H(human to human)连接,达到万亿量级。M2M业务的加入、网络的IP化、数据业务种类的增加,使通信网络的拥塞控制越来越重要。众多专家学者提出了多种拥塞控制策略,包括早期的尾部丢弃(DT)策略和后来的各种主动队列管理(AQM)机制。RED及其各种变形是业界广泛研究的AQM机制[1~5]。基于排队理论建模并评估AQM机制,是AQM研究的一个分支,对于AQM的布置、实施具有重要意义。
Jacek建立了采用RED机制的IP网络的排队模型,得到环回时间、分组丢失概率等参量,从而得到TCP的发送速率[6]。Stankiewicz Rafa建立了WRED和RIO-C两类RED机制的分析模型作为区分服务网络的丢弃机制,用于M(n)/M/1/K和M(n)/D/1/K排队模型中[7]。Singh Mohit B.等人利用有限状态马尔科夫链,建立一个分析模型捕捉了RED队列的分组丢失行为,利用迭代等式得到了闭合解[8]。Lin Guan等人在RED机制的分析建模中做了系列研究,文献[9,10]研究了业务源为具有突发性和相关性的 MMBP-2且考虑了RED机制的离散时间排队系统,利用二维离散时间马尔科夫链建模RED机制,将分组丢失率反映在到达率的减少上。文献[11]建立了一个输入为 N个 MMBP-2叠加源的离散时间排队系统,建模分析RED和WRED机制的性能。文献[12]在文献[11]的基础上建立了一个队列管理方案,通过调整队列的阈值来改变顾客到达速率,从而实现对平均排队时延的控制。Hussein等人的工作与上述研究不同,他们考虑了实际网络由多节点构成的情况,建立了基于DRED机制的两队列串联的离散时间排队网络,分析并比较了3种AQM机制的性能[13]。
综上可以看出,大部分 RED理论分析模型都是基于单个节点的排队模型,他们假设各个节点是互相独立的。然而在实际的IP核心网中,数据分组要经过多个路由器的转发最终到达目的地,一个节点的输出作为另一节点的输入,节点间具有关联性,单节点排队模型显然无法建模这种关联性,而且网络运营商和用户更为关注所感知到的端到端性能指标,单节点模型无法得到端到端参数。因此本文提出了一个离散时间的串联排队网络模型,建模采用RED、指数RED(ERED)机制的IP核心网络。与文献[13]建立的两队列串联的离散时间排队网络不同,本文考虑了节点(路由器)具有有限的缓存空间的情况,这种条件下,串联排队网络不具备乘积型解,不适合用Jackson定理求解。本文采用了分析近似方法中的分解方法求解了该非乘积型解的离散时间串联排队网络,推导了指数RED算法,分析比较了DT机制、RED机制和ERED机制及不同的参数设置对AQM性能的影响,分析了具有不同自相关特性的业务源对 AQM 性能的影响。本文研究成果对IP承载网络拥塞控制机制的选择、参数的设置有指导意义。本文还提供了根据每个节点的性能指标发现网络瓶颈的理论分析方法。
2 模型建立
2.1 业务源模型
突发性和相关性是描述业务源的2大重要性质。Poisson过程不适于建模基于分组交换的现代通信系统中的业务,为了既能描述业务的突发性和相关性又可以得到可行的解析性,本文用二态马尔科夫调制的伯努利过程(MMBP-2)作为业务源模型。MMBP-2模型可以用一个四元组(p,q,α,β)来完全描述,可以通过选取合适的(p,q,α,β)参数,描述具有不同到达强度、突发性和相关性的业务源模型。
如图1所示,MMBP-2由2个状态组成,也可称为2个环境位相,会话到达率随一个二态马尔科夫链变化而变化,在每一个环境位相上顾客按照Bernoulli方式到达,处于环境位相1时到达速率为α,处于环境位相2时到达速率为β,可用转移概率矩阵P和到达概率矩阵Λ来描述MMBP-2模型。
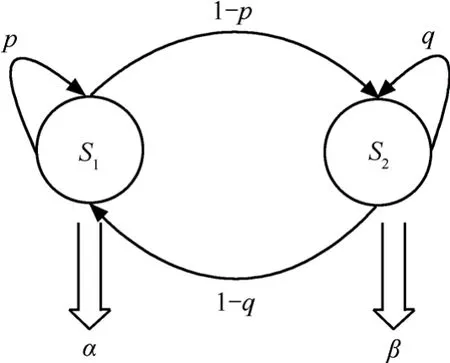
图1 MMBP-2业务源模型
MMBP-2业务源的 4个统计量,平均到达率ρMMBP-2、到达时间间隔的平方变差系数 CM2MBP-2(简称SCV)、到达时间间隔的一阶自相关系数φ(1)和每个时隙内到达顾客数的k阶自相关系数φ(k)的表达式分别为[14]
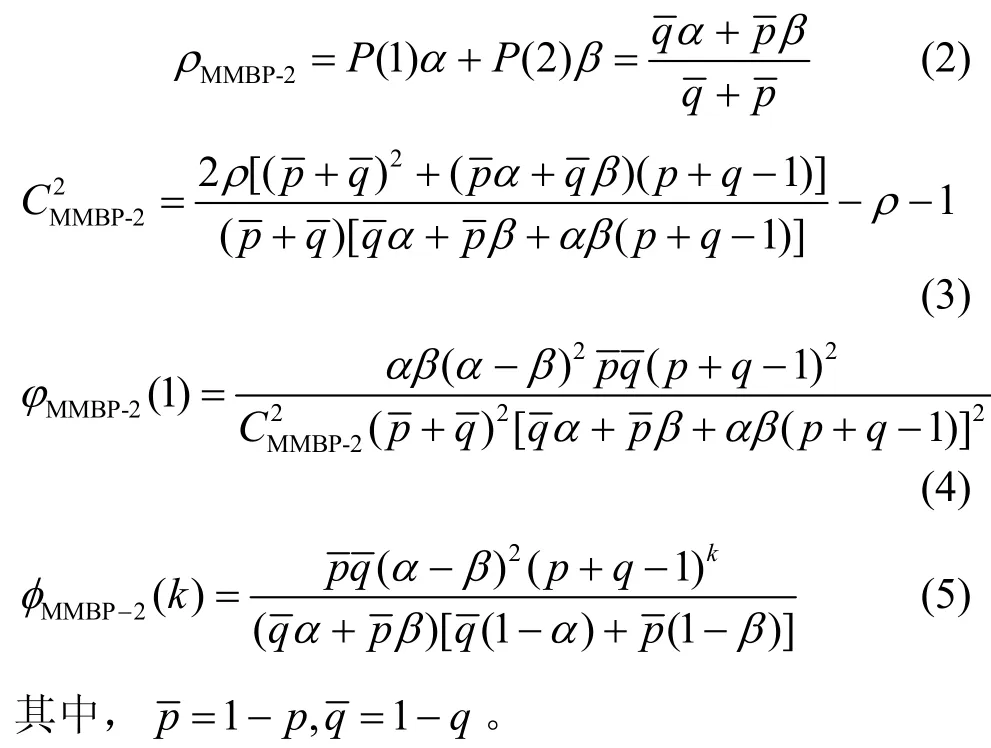
2.2 RED和ERED机制
RED机制中设置了2个阈值 th1和 th2,当数据分组到达缓存后,若缓存长度小于 th1则直接进入缓存,若缓存长度在 th1和 th2之间时则线性分组丢失,若缓存长度大于 th2则将该分组丢弃,分组丢失函数见式(6)。
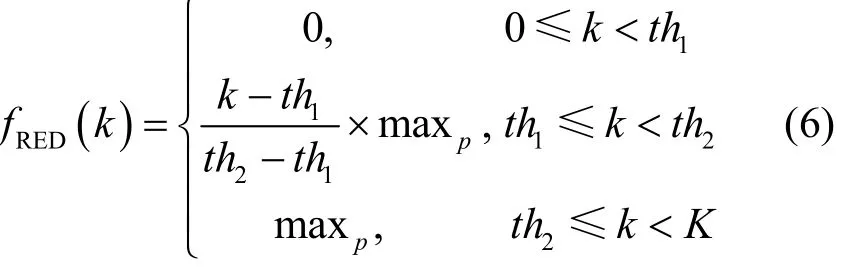
为了克服RED机制的参数设置敏感问题并能更好地在吞吐量、时延和分组丢失率几个性能指标上折衷,本文还研究了指数RED机制的分组丢失函数。定义一个一般的指数函数 F (k),是一个关于缓存长度k的函数,其中,a为底数,各个系数 ci待定。
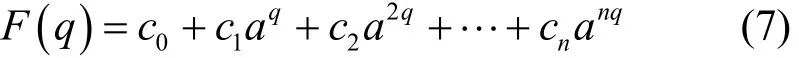
在确定该非线性分组丢失函数的各个系数应满足以下2个原则:为了避免链路利用率过低,当队长接近 th1时分组丢失函数的斜率应该较小;为了避免连续分组丢失,当队长接近 th2时分组丢失函数的斜率应该较大,因此可以得到下面的边界条件:
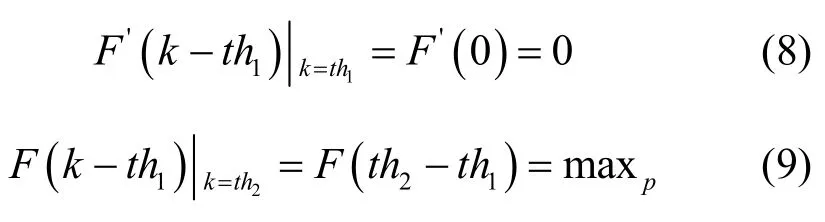
考虑到初始条件,有:
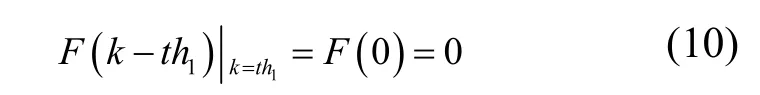
根据式(8)~式(10)可以确定指数分布中 3个系数,有:
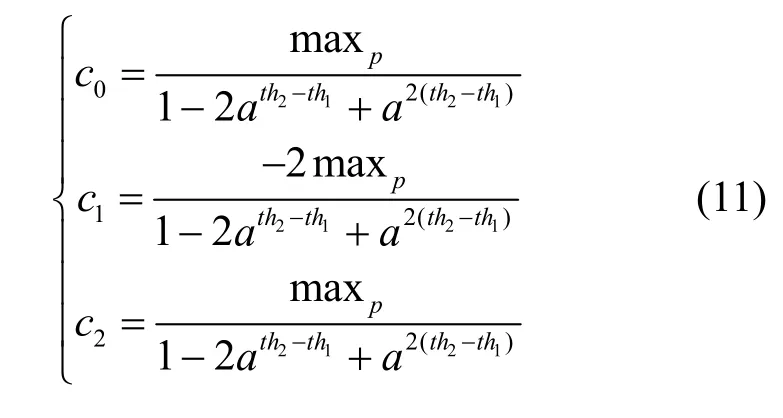
最后,得到ERED机制的分组丢失函数为
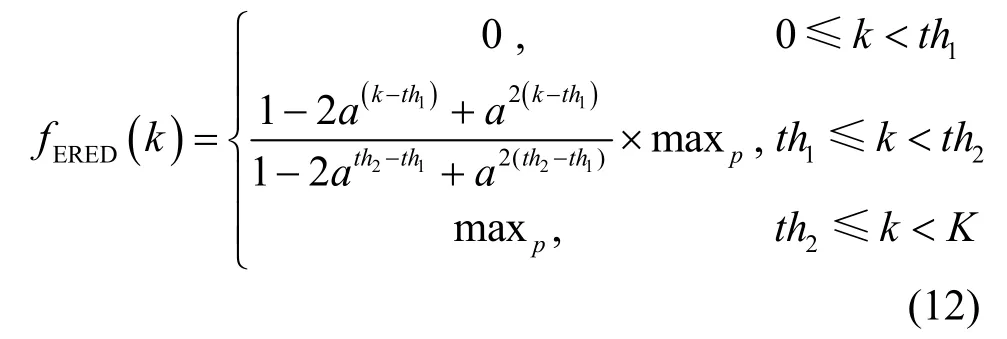
2.3 系统模型
为了分析的简便性,本文假设数据分组在 IP核心网中的路由是预先确定的,一个路由器的输出作为下一个路由器的输入,此外考虑到现代和未来的通信系统都是数字通信系统,更适于用离散时间排队论来建模,因此本文建立了离散时间有限容量的串联排队网络来建模多节点串联 RED(ERED)机制,如图2所示。串联排队网络共由M个节点串联而成,输入的业务源模型为MMBP-2模型,服务器i的服务时间分布服从参数为σi的几何分布(σi表示不成功服务的概率), Ki为节点i的最大缓存容量,包括正在被服务的顾客, i = 1 , 2,… ,M 。当顾客到达某队列时,顾客按照 RED(ERED)机制进入队列或者丢弃,顾客以先来先服务(FIFO)方式服务。
本文提出的离散时间串联排队网络由于考虑了有限的缓存空间,且加入了AQM机制,导致该串联排队网络不具有乘积型解。本文采用了分析近似方法中的分解方法将图2的串联排队网络分解为图 3,分解方法的核心思想是将一个串联排队网络分解成若干个独立的子网络,将原排队网络中各个节点间的关联反映在分解后的独立子网络的到达模型上。通过单节点排队模型的求解,离去过程分析和参数拟合方案可以将每个节点的离去过程拟合为另一个MMBP-2模型,以此类推,最终可以求解串联排队网络,其关键在于确定中间节点的到达过程。
3 模型求解
3.1 单节点排队模型求解

图2 串联排队网络模型
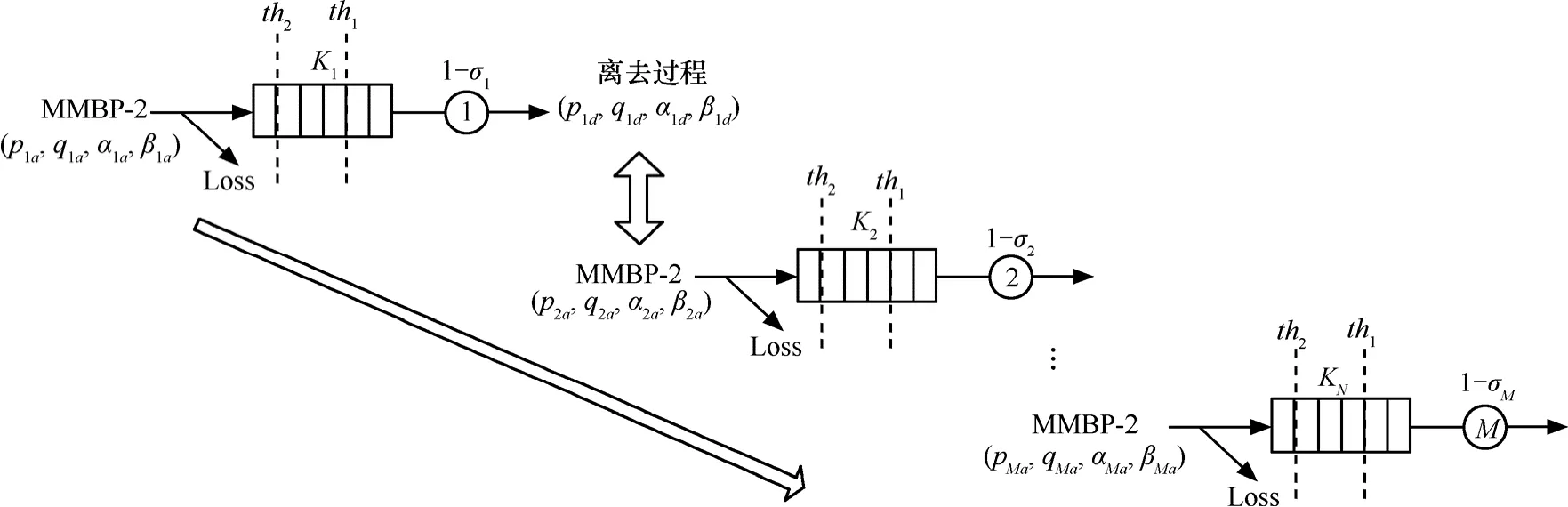
图3 串联排队网络的分解模型
本文建立了离散时间的排队模型,首先在以时隙划分的时间轴上定义该排队系统的入口协议。如图4所示,顾客总是在服务时隙的始端开始服务,在服务时隙的末端完成服务且服务时间服从参数为σ的几何分布。同时到达过程也定义在一个以相同时隙大小划分的时间轴上(不要求2个时间轴起点重合,但要满足时隙大小相同),是一个可以用四元组(p,q,α,β)描述的MMBP-2模型,假设到达过程的时隙边界与服务时隙的边界相互交替,这里规定到达空队列的顾客不能立即接受服务(即使此时服务器是空闲的),只有在下一个时隙开始时才可以接受服务,在后面的分析中,总在服务时隙的边界处查看队列所处的状态。
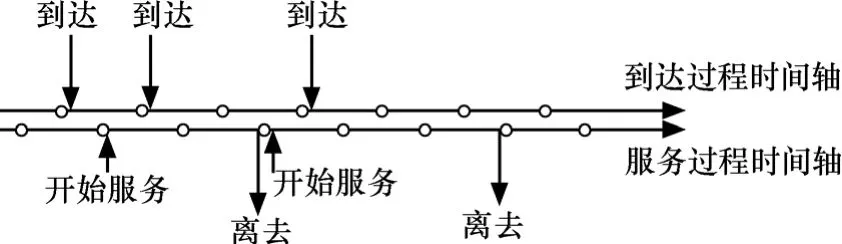
图4 离散时间排队模型的入口协议
分解后每个单节点排队模型可以表示为MMBP-2/Geo/1/Ki+RED(ERED),由于在每个单节点排队模型中考虑到了拥塞控制机制,系统会提前分组丢失,在排队模型的建立中将这种随着队长增加分组丢失率逐渐增加的现象反映为顾客到达率的逐渐减小。因此可将MMBP-2的到达概率矩阵表示为 Λ*,转移概率矩阵仍为P,有:
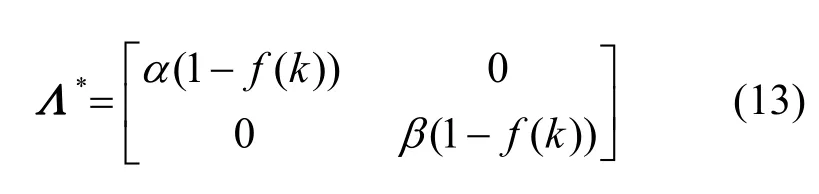
其中, f(k)表示分组丢失概率,若采用了RED机制,则为 fRED(k),若采用了ERED机制,则为 fERED(k)。
根据MMBP-2的状态转移矩阵P和速率转移矩阵Λ*可以得到其表征矩阵分别为


根据MMBP-2的表征矩阵(随缓存长度k的变化而变化)及该离散时间排队系统的入口协议,可以得到输入为MMBP-2模型的转移概率矩阵Q˜,矩阵中的每一个元素 D /R/Q以及它们的变形(R′,Q ′,R*, Q*)都是2×2的矩阵,受拥塞控制机制的影响,矩阵中的每个元素的取值都与缓存的长度k有关。
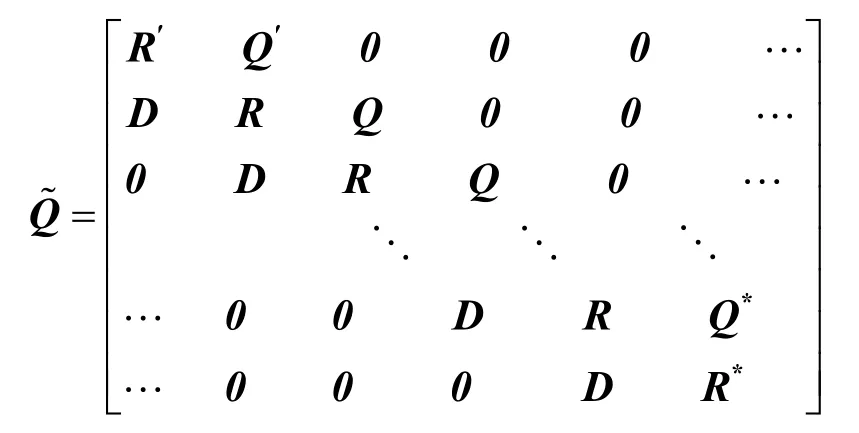
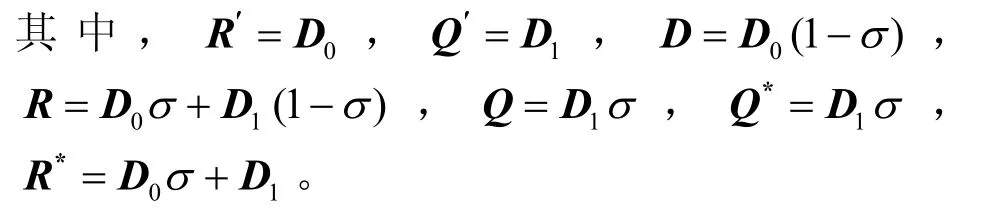
得到了转移概率矩阵Q,根据 π Q˜= π ,πe =1并利用文献[15]中提出的数值方法来得到稳态分布π= u( I-Z+ eu)-1,其中, Z=I+Q˜ /m in{Q ˜i,i},u为矩阵Z的任意一维行矢量, e =(1,1,…,1 )T。
3.2 离去过程分析和参数拟合
一个节点的离去过程由服务器的服务过程和空闲过程组成。对于2个相邻节点,前一个节点的离去过程,就是下一个节点的到达过程。本节首先推导节点的离去过程,然后再把它拟合成新的MMBP-2,作为下一级的输入过程。由于在概率空间难以得到空闲过程分布,本文在概率生成函数域求解。
根据离去时间间隔D与服务器空闲时间间隔I和服务时间S的关系,有:

根据生成函数的性质,可得:
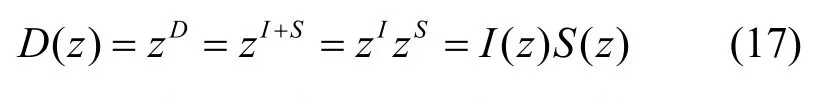
其中, S(z)为服务器服务时间的生成函数, I(z)为服务器空闲时间的生成函数,有:
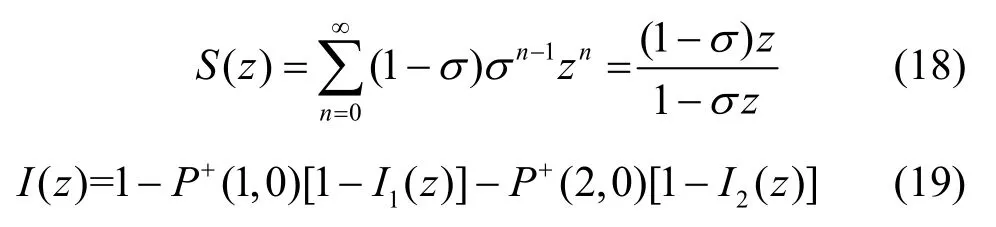
设 tn表示2次连续离去的时间间隔,根据随机理论相关知识,有:
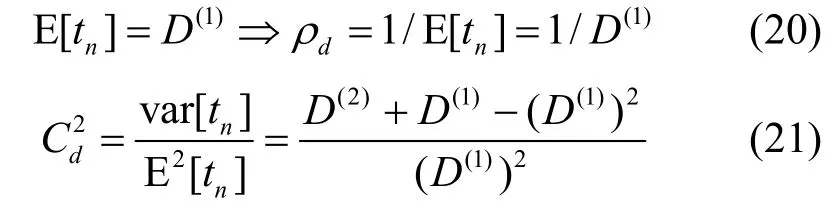
其中, D(1)和 D(2)分别为 D (z)的一阶导和二阶导。
离去时间间隔的自相关系数为
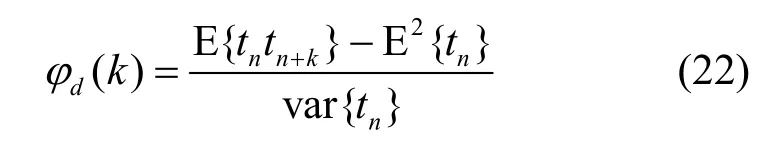
设随机变量 Xn表示在第 n个时隙离去顾客的个数, Xn= 0 ,1,则离去个数的自相关系数为
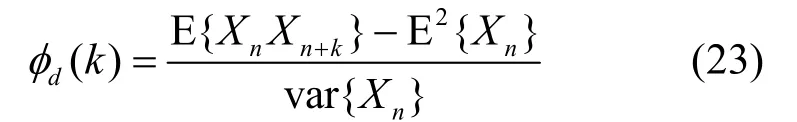
公式中涉及到的 I (z)、 I (z)、 P+( 1,0),12P+( 2,0)、E{tntn+k}、E{ XnXn+k}、E2{ Xn}和var{Xn}等表达式的计算原理可参阅文献[16]。
描述离去过程的4个统计量由式(20)~式(23)确定,把它拟合成一个新的MMBP-2。描述MMBP-2业务源的参数(α,β, p ,q )和它的统计量的关系由式(2)~式(5)确定。联立式(2)~式(5)可以求得α、β、p、q。考虑到式(4)和式(5)比较复杂,实际求解过程中本文参考了文献[16]中数值化的参数拟合方法,简化了求解过程。
3.3 性能指标
排队系统的平均队长为

系统的吞吐量为
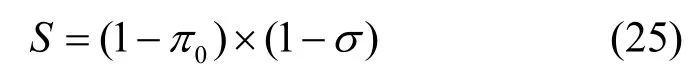
根据Little’s定理可得到系统平均时延为

排队系统的分组丢失率为

串联排队网络的端到端时延和端到端吞吐量分别为i=1
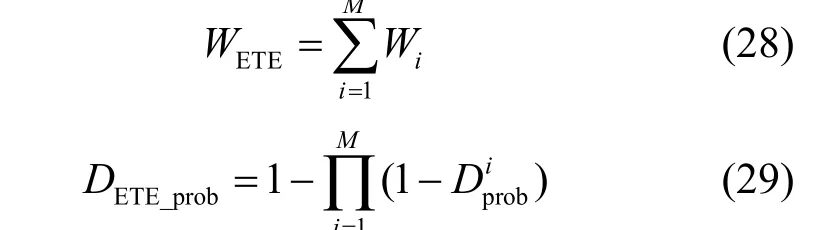
其中, W 表示串联节点i的平均排队时延。 Di表iprob示串联节点i的分组丢失率。
4 仿真结果与性能分析
仿真的网络结构为10个节点设备(路由器)级联的IP化分组交换网络,各个节点上部署了AQM机制,仿真的网络模型如图2所示。利用Matlab实现算法求解和仿真。首先根据3.1节中队列模型求解算法求得MMBP - 2/Geo/1/Ki+RED(ERED)的稳态解,然后根据3.2节离去过程分析原理和算法,在概率生成函数域求出单节点排队系统的离去过程,其中,空闲过程根据式(18)和式(19)可求得。一个节点的离去过程,就是相邻下一个节点的到达过程,根据式(20)~式(23),求出各个统计参量,再根据式(2)~式(5)即可确定下一个节点的到达过程的4个参量(α,β, p ,q )。以此类推,依次求得 10节点的稳态解,最终得到串联系统的稳态解。根据式(25)~式(29)可得到系统各节点特性和系统的端到端特性。
4.1 串联队列各节点性能分析
本节通过算法仿真分析 3种拥塞控制机制下(DT、RED和ERED)串联队列各节点性能,同时,分析业务源自相关特性对节点性指标的影响。
MMBP-2业务源的相关性、突发度等特性由参数(α,β, p ,q )决定。大量仿真实验表明,MMBP-2对参数设置敏感,由此,通过参数选择,可用 MMBP-2模拟不同特性的到达。但是业务源参数和业务源的特性的关系复杂(如式(2)~式(5)描述),因此,本文避开了理论求解,用数值实验的方法确定参数。为模拟具有不同突发度的2种业务源,首先确定了2种业务源的到达间隔的自相关系数,并假定业务源的其他3个特性参量一样,然后,根据式(2)~式(5),通过多次数值实验,确定业务源参数(α,β, p ,q )。
分别取2种业务源作为第一个队列的到达,业务源1的参数p、q、α、β分别设置为:0.964 875 84、0.968 641 75、0.010 130 000、0.937 347 45(导致了MMBP-2的ρMMBP-2=0.5,CM2MBP-2= 1 0,φMMBP-2= 0 .1,φMMBP-2= 0 .8);业务源2的参数p、q、α、β设置为:0.993 184 28、0.993 519 94、0.038 270 00、0.938 990 29(导致了 ρMMBP-2=0.5,CM2MBP-2= 1 0,φMMBP-2= 0 .4,φMMBP-2= 0 .8),可见,业务源 1、2到达间隔的自相关系数分别为0.1和0.4,根据流量的自相似理论,可以定性地认为,业务源2的突发度大于业务源1的突发度,2个业务源其他特性参量相同。
服务器的服务时间服从几何分布。考虑到分组丢失的影响,同时为了研究服务速率对节点关系。串联的10个节点的服务器不成功服务的概率从0.1逐渐增加到 0.55,步长为 0.05,即服务概率从 0.9线性下降到0.45。 AQM机制分组丢失控制参量为th1=6, th2= 1 8, K = 2 5,maxp= 0 .2, a = 1 .2。
图5为串联网络各节点的平均业务到达率。总体看,对于3种AQM机制,各个节点的业务到达率逐渐减小,RED机制到达率减小趋势最明显,而且自相关系数大的业务(可以认为突发度大,对应3条实线)的到达率减小趋势更明显,也就是分组丢失率更大。
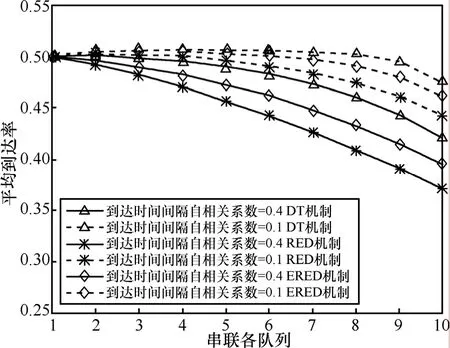
图5 不同自相关系数下不同拥塞控制机制的平均到达率
图6 ~图9给出了3种分组丢失机制下,串联排队网络中各个节点的平均队长、吞吐量、平均时延和分组丢失率,从中可以看出:排队网络中各节点的平均队长、平均时延和分组丢失率均有所增加,吞吐量减小。服务率减小是造成队长、时延、分组丢失增加的原因之一;在串联排队网络的前8个节点中,业务源1的各项性能指标皆优于业务源2,这是因为突发度大的业务对系统性能要求高,在相同的系统环境下,其性能指标劣于突发度小的业务。但串联排队网络中节点9和10的性能急剧恶化,这是因为在这 2个节点服务率和到达率相近。队列 9和节点10时服务速率分别降为0.5和0.45,由图5可知DT拥塞控制机制下2个节点的到达速率分别为0.49和0.47;自相关系数小的业务由于在前8个节点丢弃的数据分组较少,导致节点9和节点10的平均到达率较高,甚至大于服务率,因此在节点 9和节点10,自相关系数小的业务的性能急剧恶化。
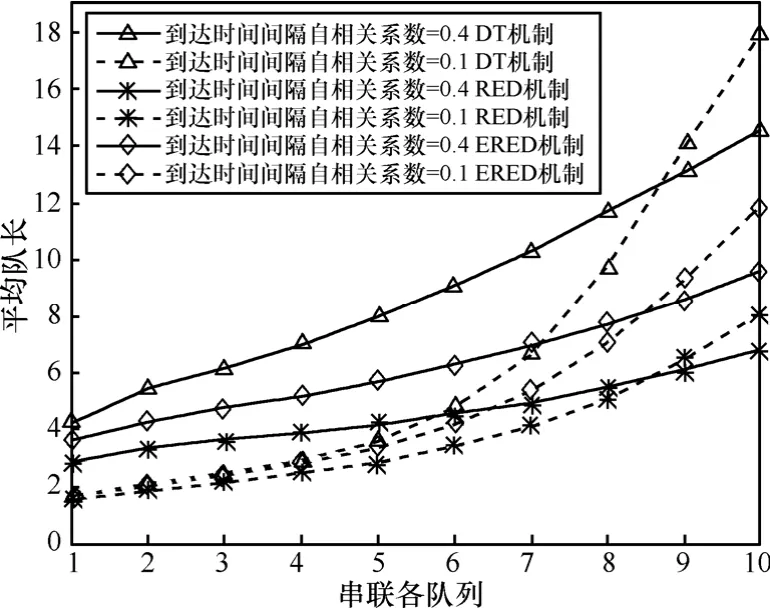
图6 不同自相关系数下不同拥塞控制机制的平均队长
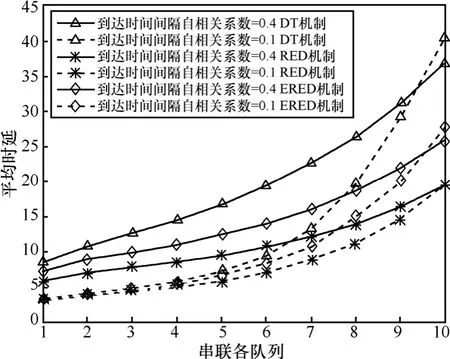
图7 不同自相关系数下不同拥塞控制机制的平均时延
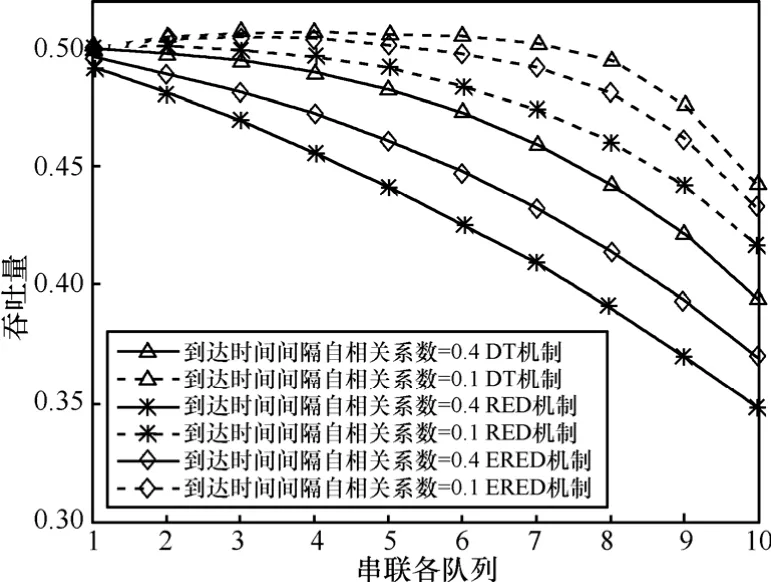
图8 不同自相关系数下不同拥塞控制机制的吞吐量
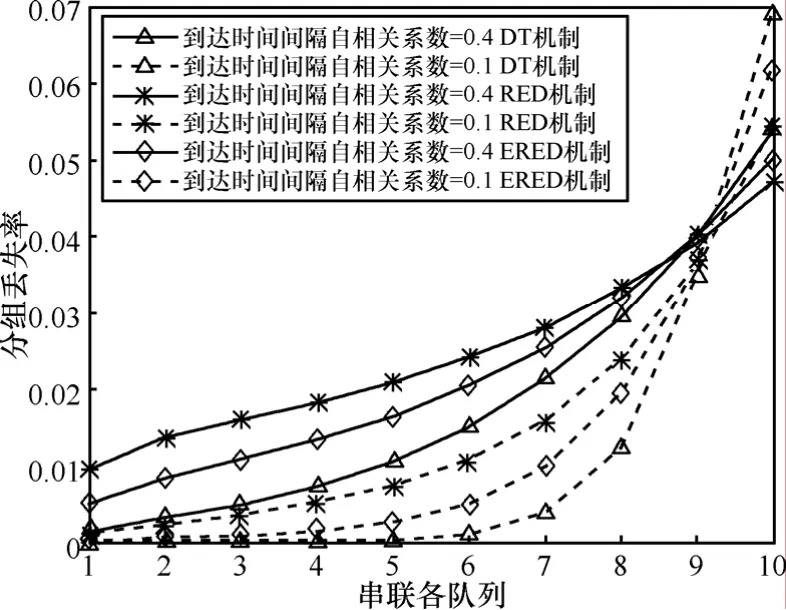
图9 不同自相关系数下不同拥塞控制机制的分组丢失率
4.2 AQM机制端到端性能分析
本节给出了3种拥塞控制机制中不同的参数设置对串联排队网络端到端性能指标的影响。图 10和图11给出了随着最大分组丢失率maxp的不断增大,网络的端到端时延和分组丢失率的变化趋势。由于DT拥塞控制机制不受maxp的影响,因此其端到端时延和分组丢失率为直线。对于 RED机制和ERED机制来说,随着maxp的线性增加,串联排队网络的端到端时延下降,但是,端到端分组丢失率增加。图12和图13给出了网络的端到端时延和分组丢失率随着 th2- t h1的增大而变化的情况。从 2图中可以看出端到端时延和分组丢失率几乎是随着 th2- t h1的线性增加而线性变化的,不同的业务有不同的QoS要求。实时音、视频业务对时延及其抖动敏感,非实时业务,比如,M2M 的数据业务对时延要求较低。实际应用中,可以根据业务的要求,选择AQM算法,设置AQM参量。图10~图13说明相对于RED机制,ERED机制可以更好地在时延和分组丢失率间取得折衷。此外,无论应用哪一种AQM机制,突发度小的业务源1的端到端性能明显优于突发度大的业务源2的端到端性能。
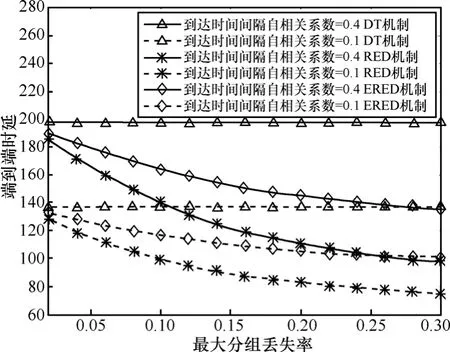
图10 不同自相关系数下不同拥塞控制机制的端到端时延
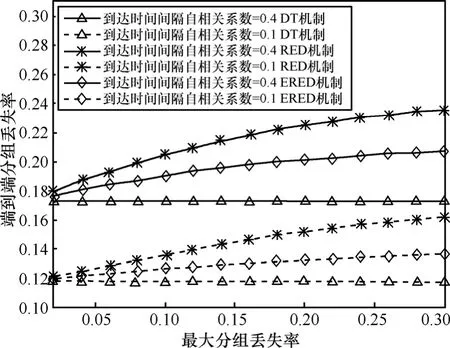
图11 不同自相关系数下不同拥塞控制机制的端到端分组丢失率
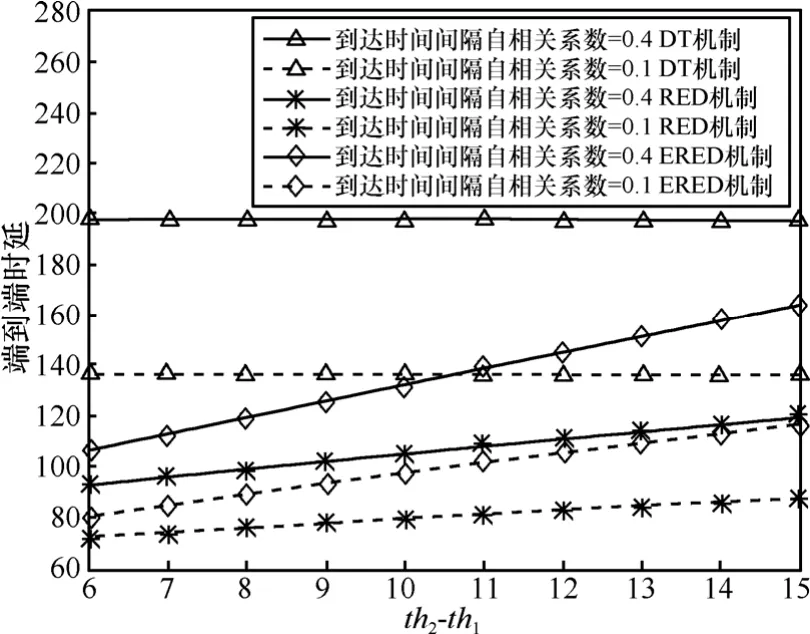
图12 端到端时延随着th2-th1变化情况
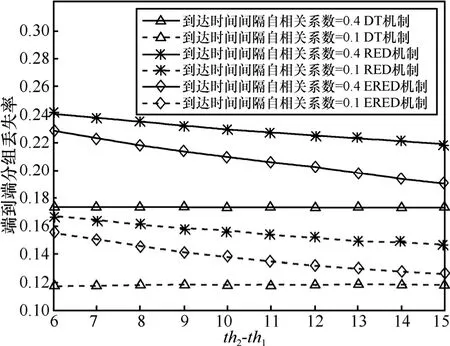
图13 端到端分组丢失率随着th2-th1变化情况
5 结束语
本文采用建立离散时间的串联排队拥塞控制机制的分析模型,选取了具有不同突发度的2种业务源作为系统输入。将拥塞控制机制中的分组丢失概率随缓存中顾客数的增加而增大的现象反映为排队系统中顾客到达概率的减小,利用分解方法求解了带有拥塞控制机制的串联排队网络。此外分析了不同的业务源特性、服务速率及参数设置对串联拥塞控制机制的影响,特别是,得到了系统端到端性能指标。在实际应用中可根据业务源的突发性和相关性、业务类别及其QoS需求合理地选择拥塞控制机制并设置合适的阈值及分组丢失概率,在时延和分组丢失率间取得更好的折衷。文章成果可用于IP网络的性能分析和网络设计与优化。将更深入地研究业务源建模,使系统模型逐步逼近实际网络。
[1] BRADEN B, et al. Recommendations on Queue Management and Congestion Avoidance in the Internet[S]. IETF RFC 2309, 1998.
[2] HOLLOT C, MISRA V, TOWSLEY D. On designing improved controllers for AQM routers supporting TCP flows[A]. INFOCOM 2001,20th Annual Joint Conference of the IEEE Computer and Communications Societies[C]. 2001.1726-1734.
[3] ATHURALIYA S, LOW S, LI V, et al. REM: active queue management[J]. IEEE Network, 2001, 15(3):48-53.
[4] FENG W, SHIN K, KANDLUR D, et al. The BLUE active queue management algorithms[J]. IEEE/ACM Transactions on Networking(TON), 2002, 10(4):513-528.
[5] KAPADIA A, FENG W, CAMPBELL R. GREEN: a TCP Equation-Based Approach to Active Queue Managementc[R]. Technical Report UIUCDCS-R-2004-2408, University of Illinois, 2004.
[6] JACEK S. Modeling TCP/RED - approximate performance evaluation using an analytical queueing approach [J]. Systems Science, 2006,32(3):109-117.
[7] RAFA S, ANDRZEJ J. Analytical models for multi-RED queues serving as droppers in DiffServ networks[A]. IEEE Global Telecommunications Conference[C]. 2007. 2667-2671.
[8] SINGH MOHIT B, et al. A finite-state Markov chain model for statistical loss across a RED queue[A]. ICW 2005, ICHSN 2005, ICMCS 2005, SENET 2005[C]. 2005.305-310.
[9] GUAN L, AWAN I U, et al. Discrete-time performance analysis of a congestion control mechanism based on RED under multi-class bursty and correlated traffic[J]. Journal of Systems and Software, 2007,80(10):1716-1725.
[10] GUAN L, AWAN I U, WOODWARD M E. Stochastic modelling of a random early detection based congestion control mechanism for bursty and correlated traffic[J]. IEEE Proceedings on Software Engineering,2004, 151(5):240-247.
[11] LIM L B, GUAN L, et al. RED and WRED performance analysis based on superposition of N MMBP arrival proccess[A]. The 24th IEEE International Conference on Advanced Information Networking and Applications[C]. 2010.66-73.
[12] LIM L B, GUAN L, et al. Controlling mean queuing delay under multi-class bursty and correlated traffic[J]. Elsevier Journal of Computer and System Sciences, 2010, 77(5): 898-916.
[13] ABDEL-JABER H, WOODWARD M, et al. Performance evaluation for DRED discrete-time queueing network analytical model[J]. Journal of Network and Computer Applications, 2008, 31(4):750-770.
[14] RAIF O. ATM Networks: Performance Issues[M]. Artech House Publ,1993.
[15] FISCHER W, MEIER-HELLSTERN K S. The Markov-modulated Poisson process (MMPP) cookbook[J]. Performance Evaluation, 1992,18:149-171.
[16] PARK D, PERROS H G, YAMASHITA H. Approximate analysis of discrete-time tandem queueing networks with bursty and correlated input traffic and customer loss[J]. Oper Res Lett, 1994, 15:95-104.
