基于一致优化的分布式宽带合作频谱感知算法

曾凡仔，刘洁，李仁发，曾庆光

（湖南大学 嵌入式系统与网络实验室，湖南 长沙 410082）

1 引言

频谱检测是认知无线电网络的关键技术之一，其目的是快速地识别主用户（primary users）和其他的认知无线电(CR)用户之间频谱的占用情况，以方便使用暂时闲置的频谱空洞，同时要严格地保护主用户的传输且避免CR用户之间的干扰。目前，单 CR用户频谱检测技术主要包括匹配滤波器检测、能量检测和特征检测[1]。

由于无线信道衰落，包括大尺度效应、小尺度深衰落，使得单个认知无线电无法准确地感知和探测主用户的传输[2]。为了降低信道衰落以及阴影效应的影响，考虑多个认知无线电用户之间的空间分集，合作频谱感知引起学者们的注意。合作频谱感知有集中式与分布式2种，集中式的合作频谱感知由融合中心收集来自多个认知无线电用户的时域观测，然后根据收集的信息进行频谱占用决策[3,4]。虽然集中式方法性能可达到全局最优，但是感知节点需要向融合中心传送的数据量太大，而且融合中心将频谱占用决策传回所有CR的代价也非常高。除此之外，这种方法对节点失效的容忍性也不高。相比之下，分布式方案由于其较低的数据传送量以及对节点失效的顽健性而变得非常有吸引力。分布式合作频谱感知通过每个CR与其一跳邻居通信，交换感知信息，然后迭代求解频谱估计优化问题最终使得所有 CR节点的频谱感知信息达到一致(consensus)，文献[5,6]将局部频谱感知结果采用一致平均(consensus averaging)技术进行迭代平均，直到收敛并以此为频谱感知决策，这种方法由于只进行一次频谱估计优化问题，因此频谱感知性能不足。文献[7,8]在一致优化(consensus optimization)框架下，以邻居节点的时域观测作为约束通过多次迭代优化来实现合作频谱感知，其约束的目的为迫使网络中各CR节点的频谱感知结果达到全局一致与优化。这种方法在大规模密集CR网络中，由于邻居节点数目相对较多，也就是约束个数较多而造成网络的计算与通信开销较大。

同时，由于CR所分析的频谱信号是宽带（甚至超宽带）信号，若通过Nyquist采样定理进行分析，则因采样速率过高而无法分析。为此本文将在压缩采样[9]的框架下，提出一种分布式宽带频谱压缩感知算法，算法思想如下：CR网络中每个 CR节点首先根据压缩采样理论获取压缩采样，并恢复本地的频谱信息，然后通过一跳范围内CR节点之间的信息交互获取邻居节点的频谱信息，并将此信息的加权平均作为频谱估计一致优化的约束，然后通过交替方向乘子法(ADMoM, alternating direction method of multipliers)[10]求解上述优化问题来获取整个CR网络的一致频谱估计。

2 信号建模及问题的提出

考虑多跳 CR网络模型，在这个模型中，仅仅只有PU辐射信号，而CR用户在频谱感知周期内保持静默。设 CR所分析的宽带频谱的带宽为BHz，频率范围为[fl, fu]，将整个频谱分成M个不重叠的等带宽窄带子信道，其中 fm表示每个信道的中心频率。这些子信道的位置已知，但它们的功率谱密度(PSD)水平未知并且是动态变化的，其变化取决于子信道是否被占用。那些未被占用的子信道则为频谱空洞，可以供 CR用户使用。

假设认知无线网络中有I个活跃的主用户，它的传输信号记为 s(i),i=1,…,I 。有J个CR用户，那

p么第j个CR用户收到的信号为

为分析M个信道上的频率响应，对 r(j)(t)进行M点离散傅里叶变换，则第j个CR用户接收信号的离散频谱可表示为

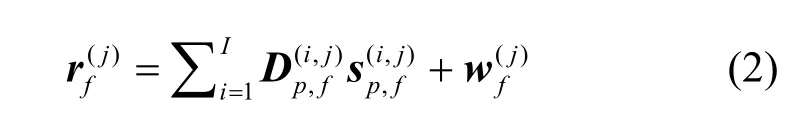
其中，D(i,j)=diag(h(i,j))是一个M×M对角矩阵信道，p,f p,fh(i,j)(t )、s(i)(t )和w(j)(t )分别是 h(i,j)、s(j)和w(j)(t)pp,ffp,f p,f f的频域离散形式。定义和，式(2)可以简写为

给定式(3)中的接收信号，频谱感知任务归结为估计频谱 sp,f。

3 分布式压缩频谱感知

3.1 压缩采样

压缩频谱感知的第一步为每个CR利用个压缩采样矩阵 sc(j)从r(

(t)j)中收集K×1时域样本向量 xt(j)，其中 Sc为K × M（K＜M） 的随机采样矩阵，具体采样过程如式(4)所示。

其中，M×1维向量 r(j)是r(j)以奈奎斯特采样率fNyqt(t )抽样得到的离散信号。

设 FM是 M点的离散傅里叶变换矩阵，则

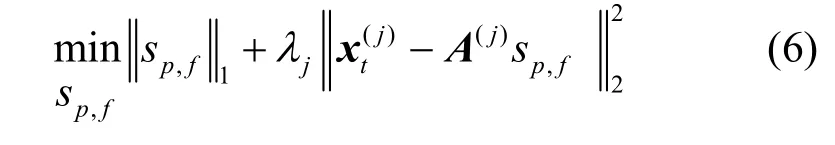
其中，λj为权系数。

在本文中，CR用户通过所有CR用户之间的合作融合各自观测来联合恢复信号 sp,f。这种观测融合比决策融合能产生更大的合作增益[8]。

3.2 基于一致优化的分布式频谱感知算法

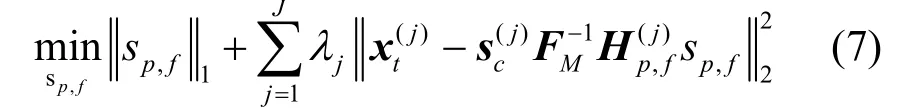
和式(6)相比，优化问题（式(7)）中的第二项包含了J个正则化项。上述问题通过加入所有CR用户的线性测量方程来得到全局最优解，但是实施起来代价昂贵。融合中心不但需要获得所有CR用户的观测，而且需要知道所有 CR用户的采中存在J项最小二乘项，那么一旦合作用户的数量比较大时，就将产生巨大的计算负担。

为了克服集中式融合方案中的弊端，只使用一跳邻居节点内的局部通信来进行合作感知，从而提出了一种分布式感知算法来估计频谱。算法通过用户间的合作和融合，采用一致优化技术使得各 CR用户j保存的频谱 sp,f的副本。设 G=（N,ϵ）为无向图，其中 N = ｛ 1,…,J ｝，（j,k）∈ϵ为一跳通信范围内的无序CR节点对， Nj= ｛ k |（ j, k ）∈ϵ｝表示CRj的一跳通信邻居集合。则此时，与目标函数（式（7））不同的是，每个CR用户j在本地执行下面的一致

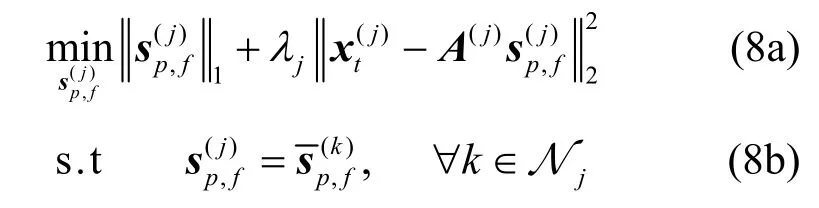
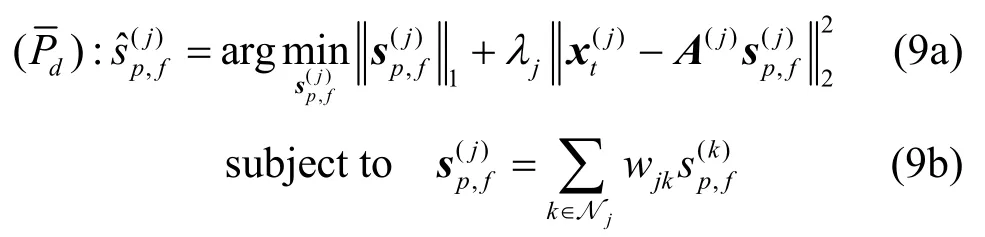
比较优化问题(Pd)与可知，优化问题的约束个数变为一个，因此有望降低计算开销。其中wjk是与无向图的边 (j , k )相关的加权系数。由于为无向图，因此定义加权系数矩阵W，其第 (j , k )元素即为wjk且有 W 1T=1，其中1为一维向量。

3.3基于交替方向乘子法的分布式频谱感知算法实现

现在给出优化问题（式(9)）的迭代实现。上述优化问题的增强拉格朗日函数如下：

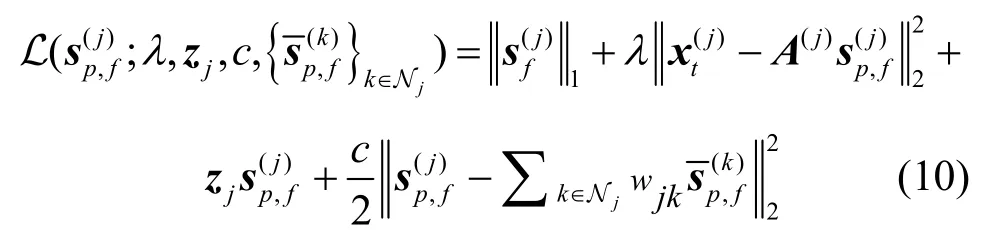
其中， zj和c为拉格朗日和增强拉格朗日乘子。设s(

j)(t)来表示第t次迭代 CR用户j的临时频谱估p,f计。运用交替方向乘子法[10]，每个CR通过求解优化问题(式(11))迭代更新它们的 s(j)(t)p,f

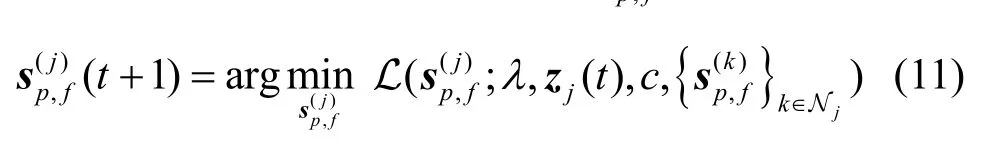
同时使用基于梯度的迭代来更新乘子：

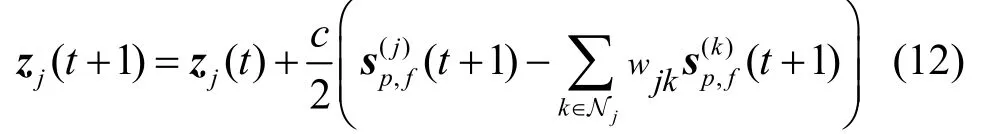
式(11)和式(12)中的迭代步骤构成了分布式合作压缩频谱感知算法。在第t次迭代开始的时刻，每个 CR用户 j从他们的邻居 k ∈Nj中收集s(k)=s(k)(t)，求解式(11)对应的二次优化问题，产p,fp,f生了最新的本地评估 s(j)(t+1)，然后根据式(12)更f新本地乘子向量 zj(t )。所有的CR用户广播稀疏频谱估计 s(j)(t+1)给它们的一跳邻居用户，然后继续f下一轮迭代，直到收敛。

算法1 分布式合作压缩谱感知算法。

初始化 每个CR样本在本地通过压缩采样获取时域观测 xt(j),设置参数λ、c和β。初始化频谱估计 s(j)(0) = 0以及乘子向量 z (0) =0 ,∀jp,fj

迭代：

for t=0, 1, …

所有的 CR通过式(12)和式(11)更新 zj(t )和s(j)(t+1)。p,f

所有的CR广播 s(j)(t+1)至一跳相邻的CR。p,f

end for

决策：一旦收敛，每个CR获得全局的频谱估计sˆp,f=s(pj,)f( ∞ ), ∀j 。然后通过阈值化 dˆp,f={sˆp,f≥ηs}来判断频谱使用情况。

上述算法是收敛的，具体收敛性证明见附录。

4 仿真实验

4.1 仿真实验设置与算法性能评价指标

设CR所分析的宽带频谱带宽为BHz，频率范围为[fl,fu]，将整个频谱分成M个（M=20）不重叠的等带宽子信道｛fm｝mM=-01，其中 fm表示每个信道的中心频率。假定整个宽带信道 h(i,j)(t),∀i,j为频率p选择性衰落信道，而每个子信道 fm上的衰落系数hi,j[m]在每一个检测周期为服从瑞利分布的时不p变信道。

CR的信噪比（SNR）定义为整个宽带上平均所接收信号功率与白噪声功率的比值。压缩比K／M为压缩采样的样本数与采用Nyquist采样速率所需样本数的比值。为了评价频谱估计的性能，采用频谱sˆp,f的均方误差(MSE)，即｝作为评价指标。对于频谱空洞检测，感兴趣的性能指标为检测概率 Pd和虚警概率 Pfa，它们通过频谱占用决策与主用户占用子信道的实际情况 dp相比来计算，具体计算表达式如下：

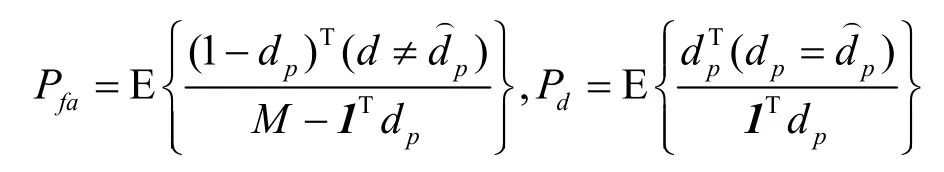
4.2 频谱感知算法性能

设主用户随机占据M个子信道中的I个，同时在感知过程中所有J个CR用户保持静默。

1) 3种频谱感知算法的性能比较

在这里，将算法1的性能与另外2种方法进行比较，其中一个是式(7)所提到的集中式融合法(fusion consensus)，另一个是文献[6]中的一致平均决策融合策略。在后一种方法中，稀疏信号 sp,f通过求解优化问题（式(6)）本地重建，此优化问题不含一致约束，而本地估计的平均值如文献[11]中的算法所示，是通过迭代的分布式一致平均算法求得。

图1和图2描述了在I=2、M=20、K=10和SNR=-5dB的情况下，3种方法的MSE和（ROC, receiver operating characteristic）的性能。从中可以得出，集中式方法表现得最好，但同时也拥有最大的计算复杂度。一致平均算法虽然实现起来很简单，但是它的性能却是三者中最差的，因为这种方法只建立在一次频谱重构的基础上。而本文提出的方法性能较好，在没有融合中心的前提下，它的ROC性能近似最优。

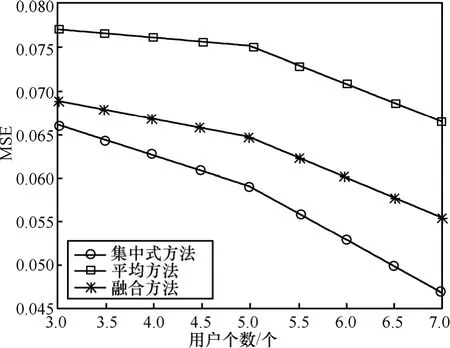
图1 给定压缩比为50%，3种频谱感知算法的MSE与CR用户个数的关系

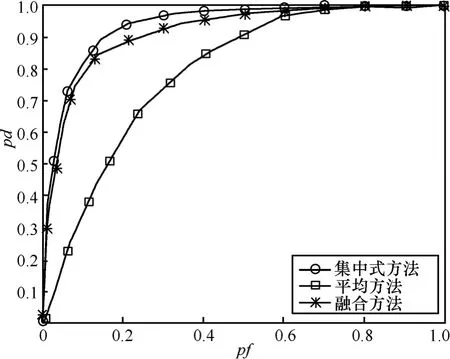
图2 给定压缩率为50%，3种频谱感知算法的ROC曲线对比

2) 用户合作增益与CR用户数量之间的关系

CR用户间的合作提供了空间分集增益，这能减轻由于随机信道衰弱而导致的性能退化，从而减轻隐藏终端问题。图3为给定I = 2, M = 20, K = 10，SNR =-5 dB，不同CR用户数下，本文提出算法的ROC曲线。很明显，在同样的虚警概率下，检测概率随着CR用户J数量的增加而增加。

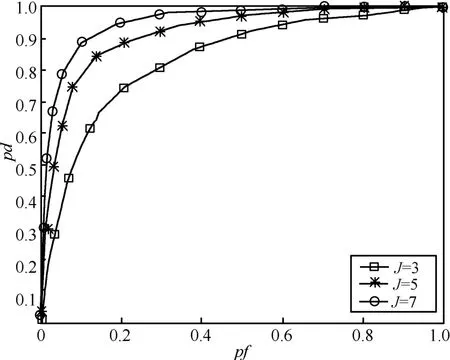
图3 本文提出算法的ROC曲线与CR用户数之间的关系

3) 稀疏信号恢复的性能与SNR和压缩率之间的关系

本文提出的频谱检测算法中一个重要的特点是引入了压缩采样来减轻宽带频谱感知中CR用户的采样负担和能量损耗。但是从另一角度看，压缩又导致了性能的退化。图4和图5为给定M=20，I= 2，J=3时，ROC曲线与压缩率的关系。由图可知，当SNR=-5dB，K=10时，即压缩率（K/M）为50%时，便可以足够精确地恢复频谱。

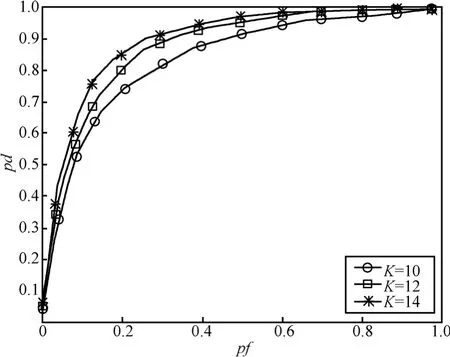
图4 本文提出算法的ROC曲线与压缩率之间的关系

5 结束语

考虑到因无线网络的频谱利用率较低而导致认知无线电所分析的频谱信号为稀疏信号的特点，本文提出了一种基于压缩采样与一致优化的分布式合作频谱感知算法。压缩采样的使用有效地降低了采样率需求，使得宽带频谱感知成为可能。主用户的稀疏频谱仅利用一跳范围内的局部通信，通过迭代求解一致优化来恢复。特别是，引入了一种加权的一致平均约束来减少一致约束的数量，由此降低了计算负担且能加速收敛。本文提供了此算法全局收敛的证明。采用交替方向乘子法实现一致优化问题。仿真表明上述提出的分布式合作频谱感知方案能有效地感知压缩采样的频谱。

附录 算法1中收敛性的证明

为了证明在式(11)和式(12)中迭代步骤的收敛性，定义和B:= W⊗IM，IM其中 是M×M的单位矩阵，⊗是Kronecker积运算符。因此，所有CR用户的联合一致优化可表示为

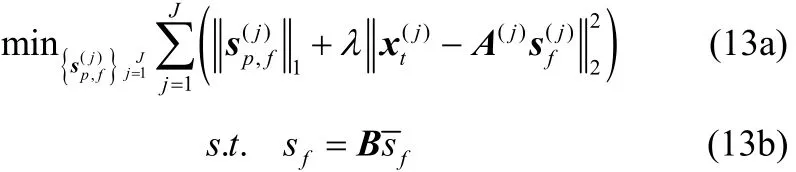
它与参考文献[10]中的优化问题的形式相同。设z为拉格朗日乘子向量，考虑增强的拉格朗日函数：

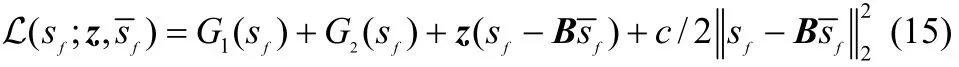
因此，交替方向乘子法的迭代步骤为

[10]中已证明，对于任何正常量c，式(16)中的ADMoM 迭代收敛于式(14)中原问题的最小值。把 G1(sf)和代入式(15)，式(16)中即可得产生算法 1中的迭代步骤式(11)和式(12)。因此，算法1全局收敛。

参考文献：

[1] HAYKIN S. Cognitive radio: brain-empowered wireless communications[J]. IEEE Journal on Selected Areas in Communications, 2005,23(2): 201-220.

[2] TANDRA R, SAHAI A. SNR walls for feature detectors[A]. New Frontiers in Dynamic Spectrum Access Networks[C]. 2007. 559-570.

[3] WANG Y, PANDHARIPANDE A, POLO Y, et al. Distributed compressive wide-band spectrum sensing[A]. Information Theory and Applications Workshop[C]. 2009. 178 -183.

[4] DUARTE M, WAKIN M, BARON D, et al. Universal distributed sensing via random projections[A]. The Fifth International Conference on Information Processing in Sensor Networks (IPSN)[C]. 2006. 177- 185.

[5] YILDIZY M E, AYSALY T C, BARNER K E. In-network cooperative spectrum sensing[A]. EURASIP European Signal Processing Conference[C]. Glasgow, Scotland, 2009.

[6] LI Z, RICHARD F, HUANG M. A distributed consensus-based cooperative spectrum sensing scheme in cognitive radios[J]. IEEE Transactions on Vehicular Technology, 2010,59(1): 383-393.

[7] BAZERQUE J A, GIANNAKIS G B. Distributed spectrum sensing for cognitive radio networks by exploiting sparsity[J]. IEEE Transactions on Signal Processing, 2010, 58(3): 1847-1862.

[8] TIAN Z. Compressed wideband sensing in cooperative cognitive radio networks[A]. IEEE Global Telecommunications Conference[C]. 2008. 1-5.

[9] DONOHO D. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52: 1289-1306.

[10] BERTSEKAS D P, TSITSIKLIS J N. Parallel and Distributed Computation: Numerical Methods[M]. Massachusetts Institute of Technology,Prentice Hall, 1989.

[11] XIAO L, BOYD S, KIM S. Distributed average consensus with least-mean-square deviation[J]. Journal of Parallel and Distributed Computing, 2007,67: 33-46.