利用加权预测的图像迭代盲解卷积
2011-11-06付东辉王毅楠
邸 男,付东辉,王毅楠
(1.中国科学院长春光学精密机械与物理研究所,吉林长春130033; 2.长春轨道客车股份有限公司,吉林 长春130062)
1 引言
天文望远镜诞生400年以来,已从小型手控的光学器材发展到由计算机控制的庞大复杂仪器。其间,有两个参数极其重要,即望远镜的口径(聚光能力)和角分辨率(图像的清晰度)。为了提高图像的角分辨率,光测设备的口径不断增大,然而,口径的增大,带来了大气湍流对成像质量影响的增强[1,2],并成为制约该领域发展的主要问题。为了解决大气湍流造成的图像退化问题,国内外很多专家学者提出了卡尔曼滤波、逆滤波、维纳滤波等方法[3],这些方法应用的前提是点扩展函数已知,而大多数情况下,由于大气湍流的高度随机性,建立一个准确的数学模型完备地描述大气湍流很困难。目前,在点扩展函数未知的情况下,盲解卷积[4,5]技术成为解决该问题的关键技术。
盲解卷积是从目标的模糊图像中确定目标的成像特性和系统点扩散函数(PSF)的一种方法,该方法能够在没有任何目标属性和大气湍流先验知识的情况下,利用单帧或多帧模糊图像估计出PSF和真实图像,具有高质量的恢复能力。目前盲解卷积方法主要有:基于马尔随机场的迭代盲解卷积[6]、多重约束迭代盲卷积[7]、模拟退火方法以及最大熵方法[8]等。前两种方法都需要对点扩展函数的支持域进行较紧的约束,而且收敛性不够好。模拟退火方法具有全局收敛性,但该方法计算量太大,难于实际应用。
本文提出一种基于加权预测的迭代盲解卷积算法,对目前性能优秀的用迭代实现盲卷积的L-R(Lucy-Richarson)算法[9]进行优化,在每次迭代结束后通过加权方法求出预测值,根据预测值计算方向加速算子,大大提高了算法的收敛速度。实验表明:该算法不仅对模糊退化图像进行了很好的复原,同时收敛速度快,具有较高的工程实用价值。
2 盲解卷积图像恢复原理
图像的退化主要来源于大气湍流,目标的运动,对焦不准确等因素的影响,盲解卷积算法使用点扩散函数来描绘这些影响。假设图像的退化模型为
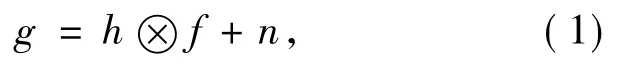
式中:g为采集到的模糊图像,h为点扩散函数,f为目标的真实图像,n为干扰噪声,⊗为卷积运算符。
由于干扰噪声的随机性,假设n服从参数为0的泊松分布,则g服从参数为h⊗f的泊松分布[10]。由此可见该泊松分布是以点扩散函数和目标亮度函数为参数的函数。估计点扩散函数和目标亮度函数就等同于估计泊松分布的参数,至此问题转化为数理统计中常见的参数估计问题。
参数估计的方法有很多,由不完全数据求总体参数的估计主要是采用最大似然估计方法。但是,由于模型中不包含任何先验知识和约束条件,最大似然估计方法的无效结果会很多,很难得到确定的理想结果。为此,需要将尽可能多并且合理的先验知识和约束条件引入泊松分布的似然函数中,本文选择目标函数的亮度值和点扩散函数值非负作为约束条件。
由于似然函数形式复杂,需要运用迭代算法实现最大似然估计过程。L-R算法是一种性能优秀的迭代算法,它使用EM(期望最大化)方法对泊松分布的参数进行最大似然估计,从而求得参数的最优估计值(即点扩散函数和目标真实图像的最优估计值)。该迭代算法简洁表示如下:
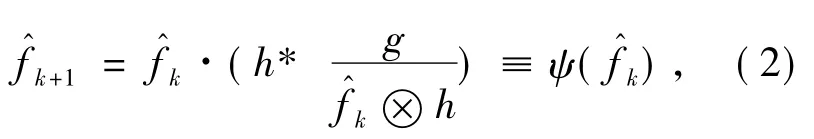
式中:f^
k为第k次迭代f的估计值,·为矩阵对应元素相乘运算符,*为互相关运算符,ψ(f^k)为L-R函数。
3 基于加权预测的迭代盲解卷积原理
3.1 算法原理
本文对L-R算法进行优化,加快收敛速度。与以往的线性加速算法不同的是,本算法在每次迭代结束后通过当前迭代位置和前一个迭代位置计算迭代方向向量和加权值,然后使用加权方法求出预测值。根据预测值计算方向加速算子,可以大大提高算法的收敛速度。优化后的L-R函数为:
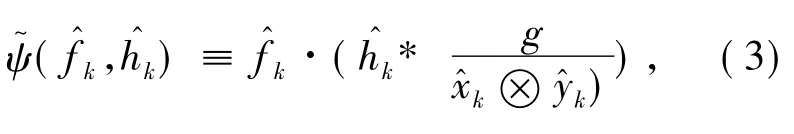
3.2 算法实现
假设n为迭代次数,f^k的初值为采集的模糊图像,h^k的初值为m×m维矩阵,所有元素都是1。基于加权预测的迭代算法具体实现如下:
①计算第k次迭代预测的恢复图像为:

式中,αk为恢复图像加速算子。
预测的点扩散函数为:

式中,βk为点扩散函数加速算子。
②计算第k+1次迭代的恢复图像估计值为:
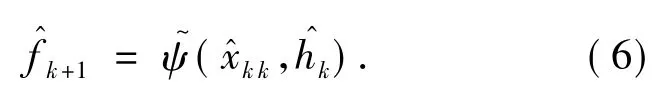
以及点扩散函数的估计值:

③计算恢复图像方向算子:
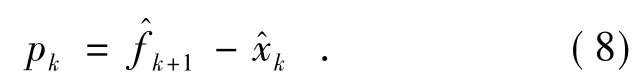
④计算点扩散函数的方向算子:
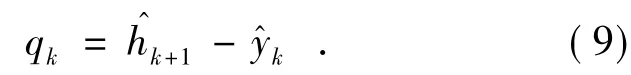
⑤更新加速算子:
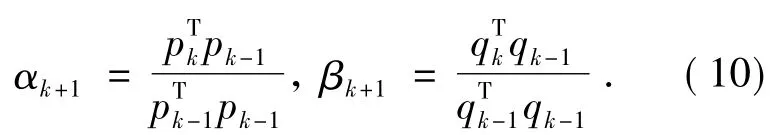
⑥k++:
如果k<n执行步骤1;

图1 盲解卷积图像恢复实验Fig.1 Restoration results of turbulence-degraded image
4 图像恢复实验
利用本文提出的算法和L-R算法对大量深空探测望远镜实拍退化图像进行了盲解卷积图像恢复实验,图1为对128×128大小图像的恢复结果。
可以看出,本文算法与L-R算法相比,达到了相近的恢复效果,证明本文算法的加速处理并没有影响图像恢复性能。
5 时间性能分析
采用L-R算法和本文算法对不同大小的图像进行图像恢复处理,在达到相近效果的情况下,对比了两种算法的迭代速度。如表1所示。

表1 L-R算法与本文算法的迭代次数比较Tab.1 Comparison of times iterated for algorithms
由表1可以看出,对于64×64大小的图像,本文算法的迭代次数减少约495/46=10.7倍,即运算速度提高约10.7倍;对于为128×128大小的图像,本文算法迭代次数减少约9 875/225=43.8倍,即运算速度提高约43.8倍。由此可见,随着图像的增大,采用本文算法的计算速度提高更加明显。
6 结论
本文提出一种基于加权预测的迭代盲解卷积算法,对目前性能优秀的用迭代实现盲卷积的L-R算法进行优化,在每次迭代结束后通过加权方法求出预测值,根据预测值计算方向加速算子,从而大大提高了算法的收敛速度。实验表明:该算法不仅对模糊退化图像进行了很好的复原,同时收敛速度提高约43.8倍,具有较高的工程实用价值。
[1]BANHAM M R,KATSAGELLOS A K.Digital image restoration[J].IEEE Signal Proc.Mag.,1997,14:24-41.
[2]FRIEDEN B R.An exact linear solution to the problem of imaging through turbulence[J].Opt.Commun.,1998,150(1-6):15-21.
[3]余国亮,张天序,洪汉玉,等.基于贝叶斯理论的湍流退化图像复原方法研究[J].中国图象图形学报,2005,10(9):1171-1177.YU G L,ZHANG T X,HONG H Y,et al.Investigation on restoration method for turbulence-degraded image using bayes theorem[J].J.Image and Graphics,2005,10(9):1171-1177.(in Chinese)
[4]宋向,袁红颖,耿则勋,等.基于双树复数小波变换的多帧迭代盲解卷积算法[J].遥感信息理论研究,2011(2):14-19.SONG X,YUAN H Y,GENG Z X,et al.Multi-frame IBD algorithm based on the dual-tree complex wavelet transform[J].Remote Sensing Information Theorem Res.,2011(2):14-19.(in Chinese)
[5]丁左红,郭汉明,高秀敏,等.基于维纳滤波的迭代盲解卷积[J].光学与光电技术,2010,8(5):24-27.DING Z H,GUO H M,GAO X M,et al..Iterative blind deconvolution based on wiener filtering[J].Opt.Optoelectronic Technol.,2010,8(5):24-27.(in Chinese)
[6]CHEN X B,YANG SH ZH,QIAO Y L.Fast multiplicative iterative blind deconvolution based on markov random field[J].Opto-Electronic Eng.,2009,36(2):96-99.
[7]陈波,程承旗,郭仕德,等.自适应光学图像非对称图像迭代盲复原算法[J].强激光与粒子束,2011,23(2):313-318.CHEN B,CHENG CH Q,GUO SH D,et al.Unsymmetrical multi-limit iterative blind deconvolution algorithm for adaptive optics image restoration[J].High Power Laser and Particle Beams,2011,23(2):313-318.(in Chinese)
[8]PINCHAS M,BOBROVSKY B Z.A maximumentropy approach for blind deconvolution[J].Signal Process.,2006,86(10):2913-2931.
[9]陈云龙,王平,王鹏.基于L-R非线性迭代的降质图像复原算法[J].计算机工程,2010,36(4):202-204.CHEN Y L,WANG P,WANG P.Degradation image restoration algorithm based on L-R nonlinear iteration[J].Computer Eng.,2010,36(4):202-204.(in Chinese)
[10]CHAN T,WONG C.Convergence of the alternating mini-mization algorithm for blind deconvolution[J].Linear Algebra Appl.,2000,316(3):259-285.
