压缩感知理论在图像处理领域的应用
2011-11-06郭立强
朱 明,高 文,2,郭立强
(1.中国科学院长春光学精密机械与物理研究所,吉林长春130033; 2.中国科学院 研究生院,北京100039)
1 引言
随着信息社会的发展,在日常生活中会经常遇到获取、存储、处理以及传输海量信息的问题。以数码相机拍照为例,由于从CCD获得的图像数据量很大,若是直接存储,一张1G Bit的存储卡只能保存几十张照片。而若通过某一压缩算法对图像信息进行重新“表示”,即可剔除照片中的冗余信息,使一张存储卡保存成百上千张照片。这是一个典型的信息编解码过程,从数学角度来讲就是信息的变换域处理。
整个编码过程由两个步骤构成:信息的获取(包含大量的冗余信息)和压缩处理。对于信息的获取,香浓-奈奎斯特采样定理指出:信号的采样频率至少是信号最高频率的2倍时才能从采样信号恢复出原始信号。但是,在海量信息以及信号频率很高的情况下,上述采样方法会造成很大的数据冗余,同时也不得不考虑硬件成本的问题。压缩处理发生在数据被完整采集到之后,在数据压缩过程中,绝大多数的数据都要丢掉,而且压缩算法的计算量要比解压缩算法的计算量大。通过以上编码过程的分析可推出:如果能以远低于信号最高频率的采样频率来采样,采样数据量就可以大大减小,另外,如果丢弃对冗余信号的采集及压缩,直接获取压缩后的数据,那么整个编码过程会变得简单易行。
压缩感知理论(Compressed Sensing,CS)指出,如果信号在某一变换域是K-稀疏的或者说是可压缩的,那么可以设计一个与相变换基不相关的非满秩矩阵(测量矩阵)来对信号进行“测量”。该测量值的长度远小于原始信号的长度,即可利用测量值,通过求解一个凸的最优化问题来实现原始信号的重构。
CS 理论的奠基性文献是 Cades[1]、Doho[2]和Tao[3]等人于2006年发表的3篇文章。文献[1]指出,对于信号f,可以从它的部分变换域信息f^恢复出f,但前提是信号是稀疏的,而这一恢复过程就是一个典型的线性规划问题。文献[2-3]都围绕着如何从测量信号准确重建出原始信号这一主题进行讨论。文献[2]把整个信号的稀疏采样理论定义为压缩感知,研究了准确重建的基追踪算法。文献[3]给出了准确重建准则。
目前,有关CS的研究论文有百余篇之多,这些论文多侧重于测量矩阵的设计、重构算法,CS的新理论以及CS的应用研究。这里简要回顾一下具有代表性的研究成果。
文献[4]研究了测量矩阵的优化问题;文献[5]利用线性调频序列构造了测量矩阵,实现了信号的量测和重构;文献[6]讨论了测量矩阵受干扰情况下的CS理论,这种干扰不同于以往的加性噪声,而是乘性噪声,在此模型下,Herman等人给出了信号准确重建的条件。目前CS理论中,测量矩阵大多采用具有一致分布的随机矩阵。随机矩阵对信号观测后也只能以很高的概率恢复出原始信号,能否构造一个测量矩阵使得信号的重构不停留在概率这一层面,另外,用硬件产生随机矩阵等都是需要解决的问题。
文献[7]从反应-扩散方程的角度,利用曲线波阈值方法提出了一种信号重构算法;Chretien提出了交互式l1松弛算法用于信号重构[8],实验将该方法用于文献[9]所提出的再加权l1范数法和再加权最小二乘法;文献[10]给出了基于随机梯度自适应滤波架构的信号重建算法,实验结果表明:所提出的算法在准确重建和抵抗噪声等方面均优于匹配追踪等传统算法;文献[11]针对信号重构的递归硬阈值算法给出了理论分析;文献[12-13]研究了一类在正交基和非一致字典上不具备稀疏性而在冗余字典上具有稀疏性信号的重构问题;文献[14]讨论了最优基的选择问题,利用多分辨率分析的思想,采用树状结构字典对信号进行测量及重构;文献[15]对Poisson噪声下CS理论加以研究,给出了相关噪声下信号重构误差的上限;文献[16]提出了基于模型的CS理论并给出了相应的重构算法。
在应用方面,已有的文献[17-29]证实了CS理论已应用于雷达成像、医学核磁共振成像、无线通道图像传输、彩色图像成像、相位编码速度成像、视频监控、语音编码、多通道盲信号处理及稀疏信道估计等方方面面。
这里,需要注意两点:首先,表面上看CS是把传统数据的“采集”和“压缩”2个步骤合并为一步,实际上并非如此,CS中的“采集”并非奈奎斯特采样频率,而是远低于奈奎斯特采样频率进行数据采集,同时能保证数据的可恢复性。
其次,CS的初衷是针对连续信号的A/D转换,这里主要讨论离散信号的CS理论。相对来讲,它比较完善,容易理解。
2 CS理论架构
CS过程实际上是用测量矩阵A对信号x进行“测量”,得到测量向量y。具体描述如下:设x为离散信号,A=Φ^·Ψ为m×n测量矩阵,且m=n。y=A·x,其中称y为测量信号。图1为CS的实现示意图。

图1 CS的概要图Fig.1 Schematic diagram of CS
这时测量信号y的长度为m,远远小于原始信号长度n。这样便实现了对信号x的压缩。但是这样一个矩阵乘法真的“感知”到原始信号x了吗?换言之,如何从测量信号y恢复出x?回答这个问题之前,首先给出2个概念,即稀疏性和非一致性。
对于一个长度为n的离散信号x,若x中含有k个不为零的分量,并且k=n,则称信号x为K-稀疏。假设x是稀疏信号,y=x+ω,其中,‖ω‖是一个很小的常数。也就是信号y偏离稀疏信号x很小的量,则称信号y是近似稀疏的。现实生活中很难找到在时域具有稀疏性的信号。例如声音信号,图像信号,既不是近似稀疏的更不是K-稀疏的。这就需要考虑如何把不稀疏的信号“变成”稀疏的信号,从而涉及到信号的变换域表示问题。对于信号x若存在一个基(或框架,字典)Ψ,使得x在Ψ上的投影结果为近似稀疏,则称信号x是可压缩的。用数学公式表达如下:x=Ψ·α,其中,α =αs+ω,αs是 K-稀疏向量且保持了α的绝大部分能量。
信号的稀疏表示是CS理论应用的基础和前提,只有选择合适的基(字典)来表示信号,才能保证信号的稀疏性,从而保证其恢复精度。在研究信号的稀疏表示时,可以通过变换系数衰减速度来衡量变换基的稀疏表示能力。传统的Fourier变换、小波变换以及后小波理论中的各个变换的核函数都能够对信号进行稀疏表示。从数学角度来讲,信号的稀疏表示本质上是典型的逼近论问题。
2组基Φ与Ψ之间的非一致性定义表示如下:对于字典D=[Φ,Ψ],其中Φ和 Ψ是两个n×n正交矩阵。Φ与Ψ之间的一致性定义如下:Ψj分别是Φ的第i行与Ψ的第j列。上述定义给出了基Φ与Ψ中元素间相关性的最大值。μ(Φ,Ψ)的取值范围是这里所感兴趣的是μ值小的字典。非一致性要求μ值越小越好,μ值越小,说明字典中的2个基越不一致。在CS理论中,2个基间的非一致性涉及信号的感知和表达,这是有效CS系统的一个至关重要的指标。
那么如何从测量信号y恢复出x?文献[29]中的一个定理回答了该问题:
定理:设x∈in,且x在基 Ψ 上 K-稀疏,x=Ψ·α。在Φ中,等概率随机地抽取m行,得到一个m×n矩阵。如果m≥c·μ2(Φ,Ψ)·k·log(n),c为某一正的常数。那么x会以很大的概率从y中恢复出来。
可以通过如下的线性规划问题来重构x:
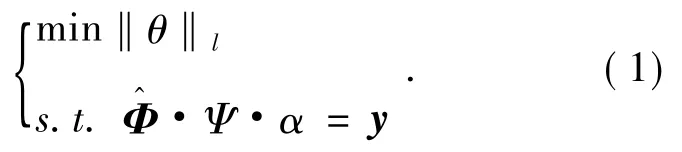
由上述定理可推出:要把原始信号x从测量信号y中恢复出来,须满足x是K-稀疏的。同时也指出了在测量矩阵A=Φ·Ψ中,Φ是从正交基Φ中等概率随机地抽取m行得到的一个m×n矩阵。常用的测量矩阵有高斯随机矩阵和傅里叶随机矩阵等。综上所述,压缩感知主要由信号的稀疏表示(Ψ)、测量矩阵的设计和信号重构算法3个部分构成。
在压缩感知的3个部分中,一个合理的测量矩阵能够保证K-稀疏信号x从n维空间映射到m维空间(m=n)过程中主要信息不丢失。在测量矩阵A=Φ^·Ψ中,Ψ用于信号的稀疏表示,一般是固定的,只有A满足约束等距性(RIP)[30],才能够利用信号恢复算法准确重建出原始信号。由此,A的RIP性是通过Φ的设计实现的。RIP的定义为:
对于任意的 K-稀疏信号x,k=1,2,3,...,定义观测矩阵A的等距常量δk满足如下不等式:
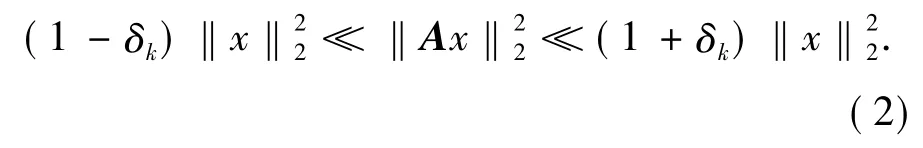
若δk<1,称测量矩阵A满足k阶 RIP。
式(2)的一个等价说法是从矩阵A任意抽取k列所构成的子矩阵是近似正交的,也可以理解为从矩阵A任意抽取k列所构成的子空间并非是零空间,否则就不能从测量信号中重构出原始信号。
测量矩阵的设计是CS理论中的难点之一,另外一个难点就是信号的重构问题。由于最优重构信号的计算复杂度很高,所以大多数研究致力于寻找近似解。求近似解有两个基本方法:一是贪婪算法,它是通过选择合适的原子并经过一系列的逐步递增方法实现信号矢量的逼近,这些统称为匹配跟踪算法。二是基跟踪算法,它是利用lp(0<p≤1)范数通过线性规划求解。第2种方法所求解更加精确,但是计算复杂度较高。
3 压缩感知理论在图像处理中的应用
这里主要介绍CS理论在成像系统、图像融合、目标识别以及图像跟踪等方面的应用。
3.1 成像系统
在成像方面,CS理论的出现激起了人们研究新型传感器的热情,CS采样对昂贵的成像器件的设计产生了重大影响。在地震勘探和核磁共振成像中,对于目标信号,将有望采用少量的随机观测次数就能获得高精度重构[31-32];取代传统数码相机拍照时采集大量像素的一种新型单像素CS相机已经得到论证。相对于CS的理论研究进展,其硬件实现还处于起步阶段[33-35]。
美国Rice大学也已经研制出单像素相机,如图2所示。该相机具有一种全新的相机结构,使用数字微镜阵列完成图像在伪随机二值模型上线性投影的光学计算。它可利用单一的信号光子检测器采样得到比图像像素点数少得多的点恢复图像,并具有对图像波长自适应的能力,这种自适应能力是传统的CCD和CMOS成像器件所不具备的。ARI-ZONA大学Baheti和Neifeld设计了具有特定功能的结构成像设备,DUCK大学研制了单景光谱成像装置。然而由于压缩重构算法的计算量比较大,难以达到实时性要求,因此实时高性能压缩感知成像系统是未来重要的研究方向。

图2 单像素相机Fig.2 Single pixel camera
3.2 图像融合
图像融合[36]是信息融合范畴内以图像为对象的研究领域。图像融合将多个成像传感器或同一成像传感器在不同模式下获取的同一场景的图像信息加以综合,获取更为精确、全面、可靠的图像描述。图像融合技术在自动目标识别、计算机视觉、遥感、机器人、自动小车、复杂智能制造系统、医学图像处理以及军事应用等领域有着广泛的应用潜力。
将不同模式下的待融合图像采用CS理论进行稀疏表示,使其在测量举证的作用下,用远小于原图像的数据量进行计算得到融合结果,采用重构算法将融合结果还原为图像表示,可节省中间融合所需的计算量,并且能够更好地利用原图像中像素间的内在联系,是一个非常值得研究的课题。
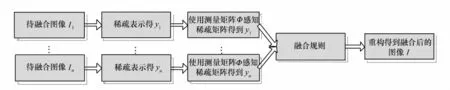
图3 CS用于图像融合的流程框图Fig.3 Frame of image fusion by using CS
3.3 目标识别
目标识别是计算机视觉和图像处理中的一个重要课题,其在军事、安防、农业、机器人控制等方面都有较好的应用前景。目标识别是指在图像/视频中寻找指定的物体(目标),对于人类来说,即使小孩子也能很轻松地在复杂图像中找到所需要的物体,哪怕是目标被遮挡、发生形变、模糊不清等情况。而对于计算机来说,这是一个非常富有挑战的课题。
文献[37]将CS理论应用于杂草种子分类识别中,文中首先对待处理的图像进行规范化,包括对图像进行校准使每幅图像中种子均在图像的正中间并且方向向上,图像均以黑色作为背景。
假定一个类中的样本都是在一个子空间中,如果第i类训练样本充足,那么任意一个同类的且不在训练集中的测试样本都可以大致由同类样本线性组合来表示,若将训练图像按行、列重组为一列,将n个不同类的训练图像组成一个矩阵,即,第i,i=1,…,n的类内训练图像为mi幅,训练图像大小为w*h,则训练矩阵A的大小为(w×,测试图像y可由式(3)得:

若测试图像y属于训练集中的某一类j,则x0中只有与j类对应的元素非零,其他元素均为零,即系数向量是稀疏向量,可用训练样本本身作为基元素去表示测试样本。求解该过程就如CS中的求解重建稀疏信号的优化方程,最后归结为求解lp范数意义下的优化问题,以获得x0的精确解或近似逼近解。
文献[31]的仿真实验结果表明:基于CS理论的分类方法优于主成分分析(PCA)+最近邻点(NN)算法以及衡量稀疏表示算法的分类效果。
3.4 目标跟踪
视频目标跟踪是使用可见、红外等被动式成像传感器实现目标测量的核心技术之一,是目标识别、视频图像的压缩编码等高层次的视频处理和应用理解的基础,也是视频监控技术自动化和实时应用的关键。目标跟踪的实质是通过对图像传感器拍摄到的视频序列进行分析,计算出目标在每帧图像中的位置、大小和运动速度。
文献[38-40]阐述了基于CS理论的目标跟踪。首先对目标进行建模,而后对后续帧图像进行相应的模型建立,将求取两模型最相似的问题转化为求取某相似参数的l1范数最小化问题,对高数据维的特征信息处理有明显优势,但是计算量大,复杂度高,是否对所有目标都具有鲁棒的跟踪效果有待于在目标跟踪方面做进一步研究。
4 结束语
CS理论自从被D.Donoho(美国科学院院士)、E.Candes(Ridgelet,Curvelet创始人)及 T.Tao(华裔科学家,2006年菲尔兹奖获得者,2008年被评为世界上最聪明的科学家)等人提出后,在信息论、信号/图像处理、医疗成像、模式识别、地质勘探、光学/雷达成像、无线通信等领域受到高度关注,并被美国科技评论评为2007年度10大科技进展之一。
本文简要说明了压缩感知理论的基本原理,及其目前在国内的发展现状和应用推广。CS理论使采集很少一部分数据并且从这些少量数据中“解压缩”出更大量信息的想法变成可能,开拓了在信息处理方面的新思路。随着其理论的完善和应用推广,其划时代的意义不言而喻。
[1]CANDÈS E,OMBERG J,TAO T.Robust uncertainty principles:exact signal recognition from highly incomplete frequency information[J].IEEE Trans.Info.Theory,2006,52(2):489-509.
[2]DONOHO D.Compressed sensing[J].IEEE Trans.Info.Theory,2006,52(4):1289-1306.
[3]CANSÈS E,TAO T.Near optimal signal recovery from random projections:universal encoding strategies? [J].IEEE Trans.Info.Theory,2006,52(12):5406-5425.
[4]ELAD M.Optimized projections for compressed sensing[J].IEEE Trans.Signal Proc.,2007,55(12):5695-5702.
[5]APPLEBAUM L,HOWARD S D,SEARLE S,et al..Chirp sensing codes:deterministic compressed sensing measurements for fast recovery[J].Appl.Comput,Harmon.Anal.,2009,26:283-290.
[6]HERMAN M A,STROHMER T.General deviants:an analysis of perturbations in compressed sensing[J].IEEE J.Selected Topics in Signal Proc.,2010,4(2):342-349.
[7]MA J W.Compressed sensing by inverse scale space and curvelet thresholding[J].Appl.Math.Comput.,2008,206:980-988.
[8]CHRETIEN S.An alternatingl1approach to the compressed sensing problem[J].IEEE Signal Proc.Lett.,2010,17(2):181-184.
[9]CCANDÈS E,WAKIN M,BOYD S.Enhancing sparsity by reweightedl1minimization[J].J.Fourier Anal.Appl.,2008,14:877-905.
[10]JIN J,GU Y,MEI S.A stochastic gradient approach on compressive sensing signal reconstruction based on adaptive filtering framework[J].IEEE J.Selected Topics Signal Proc.,2010,4(2):409-420.
[11]BLUMENSATH T,DAVIES M E.Iterative hard thresholding for compressed sensing[J].Appl.Comput.Harmon.Anal.,2009,27:265-274.
[12]RAUHNT H,SCHNASS K,VANDERGHEYNST P,et al..Compressed sensing and redundant dictionaries[J].IEEE Trans.Info.Theory,2008,54(5):2210-2219.
[13]CANSÈS E J,ELDAR Y C,NEADELL D,et al..Compressed sensing with coherent and redundant dictionaries[J].Appl.Comput.Harmon.Anal.,2010,31(1):1-21.
[14]DEYRE G.Best basis compressed sensing[J].IEEE Trans.Signal Proc.,2010,58(5):2613-2622.
[15]RAGINSKY M R,WILLETT R M,HARMANY I T,et al..Compresed sensing performance bounds under poisson noise[J].IEEE Trans.Signal Proc.,2010,58(8):3990-4002.
[16]BARANIUK R G,CEVHER V,DUARTE M F,et al..Model-based compressive sensing[J].IEEE Trans.Info.Theory,2010,56(4):1982-2001.
[17]HERMAN A,STROHMER T.High-resolution radar via compressed sensing[J].IEEE Trans.Signal Proc.,2009,57(6):2275-2284.
[18]EUDER H G.On compressive sensing applied to radar[J].Signal Proc.,2010,90:1402-1414.
[19]POTTER L C,ERTIN E,PARKER J T,et al..Sparsity and compressed sensing in radar imaging[J].Proc.IEEE,2010,98(6):1006-1020.
[20]LUSTIG M,DONOHO D L,DANLY J M.Sparse MRI:the application of compressed sensing for rapid MR imaging[J].Magn.Reson.Med.,2007,58:1182-1195.
[21]LUSTIG M,DONOHO D L,SANTOS J M,et al..Compressed sensing MRI[J].IEEE Signal Proc Mag.,2008,3:72-82.
[22]GAO D H,LIU D H,FENG Y Q,et al..A robust image transmission scheme for wireless channels based on CS[J].Lecture notes in Computer Science,2010,6216:334-341.
[23]MAJUMDAR A,WARD K.Compressed sensing of color images[J].Signal Proc.,2010,90:3122-3127.
[24]HOLLAND D J,MALIOUTOV D M,BLAKE A,et al..Reducing data acquisition times in phase-encoded velocity imaging using compressed sensing[J].J.Magnetic Resonance,2010,203:236-246.
[25]MAKALANOBIS A,MUISE R.Object specific image reconstruction using a compressive sensing architecture for application in surveillance systems[J].IEEE Trans.Aerospace and Electronic Systems,2009,45(3):1167-1180.
[26]GIACOBELLO D,CHRISTENSEN M G,MURTHI M,et al..Retrieving sparse patterns using a compressed sensing framework:applications to speech coding based on sparse linear prediction[J].IEEE Signal Proc.Lett.,2010,17(1):103-106.
[27]MISHALI M,ELDAR Y C.Blind multiband signal reconstruction:compressed sensing for analog signals[J].IEEE Trans.Signal Proc.,2009,57(3):993-1009.
[28]BERGER C R,WANG ZH H,HUANG J ZH,et al..Application of compressive sensing to sparse channel estimation[J].IEEE.Commun.Mag.,2010,10:164-174.
[29]CAND E J,ROMBERG J.Sparsity and incoherence in compressive sampling[J].Inverse Problems,2007,23(3):969-985.
[30]CAND S E,TAO T.Decoding by linear programming[J].IEEE Trans.Info.Theory,2005,51(12):4203-4215.
[31]HERRMANN F J,HENNENFENT G.Non-parametric seismic data recovery with curvelet frames[J].Geophysical J.International,2008,173(1):233-248.
[32]HERRMANN F J,WANG D L,HENNENFENT G,et al..Curvelet based seismic data processing:a multiscale and nonlinear approach[J].Geophysic,2008,73(1):A1.
[33]DUARTE M F,DAVENPORT M A,TAKHAR D,et al..Single-pixel imaging via compressive sampling[J].IEEE Signal Proc.Mag.,2008,(3):83-91.
[34]AKHAR D,LASKA J N,WAKIN M B,et al..A new compressive imaging camera architecture using optical domain compression[J].SPIE,2006,6065:606509.
[35]LUSTIG M,SANTOS J M,DONOHO D L,et al..Kt SPARSE:High frame rate dynamic MRI exploiting spatiotemporal sparsity[C].Proceedings of the 14th Annual Meeting of ISMRM,Seattle,Washington,2006:2420 22443.
[36]SMITH M I,HEATHER J P.A review of image fusion technology in 2005[J].SPIE,2005,5782:29-45.
[37]蔡骋,张明,朱俊平.基于压缩感知理论的杂草种子分类识别[J].中国科学:信息科学,2010,40(增):160-172.CAI CH,ZHANG M,ZHU J P.Weed seeds classification based on compressive sensing theory[J].Science China Information Science,2010,40(s):160-172.(in Chinese)
[38]LI H X,SHEN CH H.Robust real-time visual tracking with compressed sensing[C].Proc.of 2010 IEEE 17th International Conference on Image Processing,Hongkong,China,12-15 Sept.2010:45-48.
[39]COSSALTER M,TAGLIASACCHI M,VALENZISF G.Privacy-enabled object tracking in video sequences using compressive sensing[C].Proc.of 2009 IEEE 6th International Conference on Advanced Video and Signal Based Surveillance,Genova,Italy,2-4 Sept,2009:436-441.
[40]REDDY D,SANKARANARAYANAN A C,CEVHER V,et al..Compressed sensing for multi-view tracking and 3-D voxel reconstruction[C].2008,15th IEEE International Conference on Image Processing,San Diego,CA,2008:221-224.
