星地监测网下的北斗导航卫星轨道确定

耿 涛,刘经南,赵齐乐,施 闯

武汉大学卫星导航定位技术研究中心,湖北武汉430079

星地监测网下的北斗导航卫星轨道确定

耿 涛,刘经南,赵齐乐,施 闯

武汉大学卫星导航定位技术研究中心,湖北武汉430079

提出层间链路的星间链路方式,即以轨道高度区分的不同类型卫星间链路,在MEO卫星上安装星载接收机即可接收 GEO、IGSO卫星观测数据。根据中国卫星导航系统星座构型,从卫星跟踪时间、三维位置精度因子PDOP、定轨均方差等评价指标,分别进行地面跟踪站区域和全球非均匀分布情况下的星地链路、星地链路联合层间链路、星地链路联合星间双向测距等多种场景的定轨仿真。结果显示,基于中国区域的7个地面跟踪站1 d观测值,联合波束角为41.25°的层间星间链路,GEO、IGSO和MEO定轨均方差值由6.1 m、1.3 m和5.9 m减小到1.0 m、0.8 m和2.0 m;联合卫星波束角为45°的卫星双向测距(残余系统误差为振幅30 cm的周期项),星座整体定轨精度优于20 cm。

星地监测网;精密定轨;联合定轨;PANDA;北斗卫星导航系统

1 引 言

2000年北斗卫星导航试验系统建成,2004年中国启动北斗卫星导航系统建设工作,至2012年形成由5个 GEO、3个 IGSO、4个 MEO卫星组成的区域无源服务能力,并于2020年左右形成由5个 GEO和30个非静止卫星组成的全球无源服务能力。目前,Compass-M1、Compass-G1和Compass-G3等7颗卫星的先后成功发射,标志着该导航系统稳步进入卫星组网阶段[1-2]。

导航卫星轨道确定与时间同步技术是卫星导航系统建设和运行的核心技术之一。全球均匀分布的跟踪站联合不间断观测,才能充分发挥测量技术的潜力,达到较高的定轨精度。地面跟踪站如果区域布设,卫星跟踪弧段受限,跟踪网几何观测结构较弱,导航卫星定轨精度不高[3-4]。

为克服区域定轨观测弧段受限,进一步提高导航卫星定轨精度,就必须改善几何观测结构,国内外学者对此展开了一系列理论研究和试验。这些研究可以划分为两类:①卫星双向测距[5-8];②中低轨卫星联合定轨[9-11]。针对Compass卫星星座构型特点,提出和仿真了星地链路和星间链路组成的星地监测网(图1)。星间链路按照链路的空域可分为层内星间链路和层间星间链路。层间星间链路是指以轨道高度区分的不同轨道类型之间的链路,如 MEO-GEO、MEO-IGSO等,它仅需要星载接收机,如CHAMP、GRACE等卫星计划,技术成熟,在MEO搭载星载接收机即可接收GEO、IGSO卫星观测数据。双向测距星间链路一般采用超高频U HF频段或 Ka频段以及数据收发单元等设备在卫星之间进行双向测量和数据通信,建立星间链路。

图1 星地监测网示意图Fig.1 Satellite-ground monitoring network

2 星地链路和星间链路联合定轨数学模型

对卫星的运动方程和变分方程积分,可以得到它们的参考轨道和状态转移矩阵ψ(ti,t0)。状态转移矩阵用于将不同时刻的轨道状态改正数映射到初始时刻,应满足方程

星地链路、层间星间链路和卫星双向测距的观测方程分别为

式中,y星地i、y层间星间i和 y双向测距i分别表示星地链路、层间星间链路和双向测距观测值;x星地i、x层间星间i和x双向测距i分别表示除x＊Gi之外的其他待估参数,如钟差、对流层湿延迟、模糊度、转发时延等;v星地i、v层间星间i和 v双向测距i为相应的观测噪声。

将式(1)应用到式(5),可得到联合定轨观测模型

利用估计理论求出轨道状态改正数[12],再积分运动方程即可得到关心时段卫星的位置和速度。

3 仿真说明

3.1 仿真方案

本文进行数据处理的软件是武汉大学卫星导航定位技术研究中心自主研制的 PANDA(position and navigation data analyst)软件[13]。根据Compass星座构型(5GEO+3IGSO+4MEO),仿真了3 d卫星轨道、中国区域7个测站和全球非均匀分布16个测站(图2)的星地链路(L频段)、层间星间链路(L频段)、卫星双向测距(U HF频段),先验约束信息如表1。

图2 地面跟踪站仿真示意图Fig.2 Distribution of ground tracking stations

表1 观测值仿真信息Tab.1 Systematic and statistic measurement modeling errors

3.2 卫星跟踪时间分析

表2给出不同方案下 GEO、IGSO和 MEO卫星的跟踪时间统计结果。

表2 卫星跟踪时间百分比统计Tab.2 Statistic of satellite tracked time

从表中可知:GEO卫星定点在中国上空,跟踪弧段为100%;MEO卫星围绕地心作全球运动,仅仅采用中国区域跟踪站时跟踪弧段不足40%,当联合星间链路时跟踪弧段将随着卫星波束角的增大逐渐增加,如联合卫星波束角为41.25°的层间星间链路时达到53.3%,联合卫星波束角为30°的卫星双向测距时则近为100%,与采用16个全球跟踪站相当。这意味着在地面跟踪站较少时,联合星间链路将有助于提高卫星的跟踪时间和定轨精度。

3.3 DOP值分析

精度因子(dilution of precision,DOP)反映卫星定轨的几何观测结构,是定轨精度的评价指标之一,通常采用三维位置精度因子PDOP

式中,p11、p22、p33分别为定轨法方程逆矩阵 p中有关卫星位置子矩阵的对角线元素。

图3给出不同方案的卫星 PDOP值。从图中可知:当仅采用中国区域7个跟踪站时,GEO、IGSO和MEO卫星 PDOP值分别为40.9、59.5和38.2;如采用16个全球跟踪站时,PDOP值分别减小到8.4、9.4和8.7,这说明采用全球跟踪网时卫星定轨精度优于区域跟踪网。

增加星间链路 PDOP值将随着卫星波束角的增大逐渐减小,如采用中国区域的7个跟踪站加上卫星波束角为 41.25°的层间星间链路时PDOP值分别减小到 32.2、46.5和 9.1,其中MEO卫星减小幅度最大;如采用中国区域的7个跟踪站加上卫星波束角为45°的卫星双向测距时三类卫星PDOP值大大减小,分别为3.1、3.2和1.0,均小于采用16个全球跟踪站的 PDOP值,但当波束角再增大时,PDOP值减小幅度越来越小。这说明在地面跟踪站较少时,联合星间链路将有可能得到优于采用全球跟踪网时的卫星定轨精度。

4 仿真结果

分别采用仅基于星地链路、星地链路联合层间星间链路,以及星地链路联合卫星双向测距三种方案进行Compass定轨精度分析。

定轨中动力学模型:EIGEN_GL04地球引力场模型8×8阶;日、月和其他行星(DE405)引起的n体引力摄动;顾及固体潮、海潮和极潮影响;太阳光压摄动采用BERNESE模型。

图3 卫星DOP值统计图Fig.3 Statistic of satellites PDOP

定轨中测量学模型:数据采样间隔为300 s;非差无电离层相位组合(LC)和伪距组合(PC)定轨;观测值加权方式随高度角而变化;分别使用白噪声和随机游走来描述钟差和地面跟踪站的对流层延迟;固定测站坐标;顾及观测值仿真加入的其他误差项改正。

定轨结果评价公式如下

式中,ΔR、ΔC、ΔA分别表示估计轨道与仿真轨道在径向、法向和切向三个分量之差,n为参与比较历元总数。

4.1 基于星地链路的卫星精密定轨

计算并统计了下述三种试验 GEO、IGSO、MEO卫星的定轨 RMS3D值(图 4),需要说明的是,这三个试验在先验信息的设置上是相同的。

试验1,采用中国区域的7个地面站1 d的观测值;

试验2,采用中国区域的7个地面站3 d的观测值;

试验3,采用全球非均匀分布的16个地面站1 d的观测值。

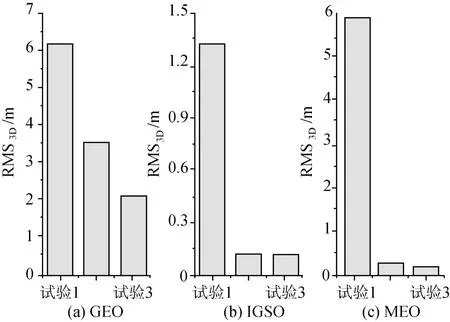
图4 基于星地链路的Compass定轨精度Fig.4 OrbitdeterminationRMS3Dfrom groundbased tracking

对比试验1和2可知:随着定轨弧段的增加,三种类型卫星的定轨精度均有不同程度的提高,这与轨道观测量的增多,以及两段连续观测数据可以对中间未跟踪到的卫星弧段施加约束,减弱单天定轨中的“末端效应”有关。其中MEO定轨精度提高幅度最大,RMS3D由5.9 m减小到0.3 m,幅度超过 95%;IGSO次之,幅度超过91%;而 GEO卫星 RMS3D仅由 6.1 m减小到3.5 m,这是因为 GEO卫星与地面站的位置几乎相对静止,几何观测结构相当差,定轨法方程严重病态,使得一些系统误差(如钟差及测站偏差等)难以精确解算和分离,即使增加观测时间带来的有效信息量也有限,从而造成定轨精度提高幅度小。

对比试验1和3可知:随着地面站的全球布设,卫星几何观测结构得到改善,三种类型卫星的定轨精度也有不同程度提高,但仍不能很好地解决 GEO卫星的精密定轨问题。

4.2 星地链路联合层间星间链路的卫星精密定轨

类似于4.1节,计算并统计下述三个试验中GEO、IGSO、MEO卫星随卫星波束角的定轨RMS3D值(图 5)。

图5 星地链路联合层间星间链路的Compass定轨精度Fig.5 Orbit determination RMS3Dfrom inter inter-satellite-links

试验1,采用中国区域的7个地面站和层间星间链路1 d的观测值;

试验2,采用中国区域的7个地面站和层间星间链路3 d的观测值;

试验3,采用全球非均匀分布的16个地面站和层间星间链路1 d的观测值。

对比图4试验 1,如再加上卫星波束角为41.25°的层间星间链路,GEO、IGSO和 MEO定轨RMS3D值由6.1 m、1.3 m和5.9 m分别减少到1.0 m、0.8 m和2.0 m。其中 GEO卫星提高幅度最大,达到84%;MEO卫星次之,提高幅度约66%。这是因为层内星间链路充分利用三类卫星的轨道高度差优势,以不同于地面站的几何层面增强了卫星几何观测结构,同时有效克服了GEO卫星由于与地面站的位置相对静止引起的定轨法方程病态问题,从而提高整个星座的定轨精度。

对比图4,试验2和3中的 GEO卫星定轨精度有大幅度提高。但IGSO、MEO卫星基本处于同一量级,这可能是因为卫星几何观测结构当采用3 d定轨弧段或者全球站跟踪时已相当强,即使再增加层间星间链路也无法得到明显改善。

4.3 星地链路联合卫星双向测距的卫星精密定轨

假设U HF天线采用全向型天线,可以接收任意方向的信号;除 GEO与 GEO之间外其他各颗卫星间均建立了双向测距(图1)。本节仿真振幅分别为30 cm、50 cm的周期项残余系统误差下两组场景,每组场景中又包含了三个试验。

试验1,采用中国区域的7个地面站和卫星双向测距1 d的观测值;

试验2,采用中国区域的7个地面站和卫星双向测距3 d的观测值;

试验3,采用全球非均匀分布的16个地面站和卫星双向测距1 d的观测值。

从表3可知当加入的残余系统误差越来越大,定轨精度也越来越差。随着卫星波束角逐渐增大,卫星观测量逐渐增多和几何观测结构逐渐改善,定轨精度逐渐变好。但当波束角由45°逐渐增大时,PDOP值减小幅度越来越小,定轨精度提高幅度也越来越小,同时波束角的增大将使得卫星系统消耗的能量越大。因此卫星导航系统建设和运行时应合理选择波束角大小和尽可能的消除各种系统误差项(如硬件偏差等)。

对照表3和图4,场景1中当加入卫星波束角为45°的卫星双向测距时,试验 1中 GEO、IGSO和 MEO定轨 RMS3D值分别为 17.1 cm、16.7 cm和15.2 cm;试验2和试验3星座整体定轨精度均优于10 cm。

5 结 论

根据Compass星座构型,进行不同跟踪网和定轨方案下星地链路、层间星间链路和卫星双向测距下的定轨分析,计算结果表明:

(1)仅使用星地链路,全球跟踪网下的定轨精度明显优于区域网,但由于 GEO卫星与地面站的位置几乎相对静止,法方程病态,采用全球站仍不能很好解决 GEO卫星精密定轨问题。

(2)星地链路联合层间星间链路,将改善卫星的几何观测结构,提高整个星座(特别是 GEO、MEO卫星)的定轨精度。基于中国区域7个地面跟踪站和卫星波束角为41.25°的层间星间链路,GEO、IGSO和MEO单天解定轨 RMS3D值由6.1 m、1.3 m和5.9 m分别提高到1.0 m、0.8 m和2.0 m,其中 GEO卫星提高幅度最大,达到84%;MEO提高了66%。

(3)星地链路联合卫星双向测距,将显著改善卫星几何观测结构,增加卫星跟踪弧段,定轨精度显著提高。当残余系统误差为振幅30 cm的周期项时,基于中国区域7个跟踪站和卫星波束角为45°的卫星双向测距,单天解星座整体定轨精度优于20 cm。

(4)在我国卫星导航系统建设和运行中,应合理选择波束角大小和尽可能地消除各种残余误差(如硬件偏差等)。

表3 星地链路联合卫星双向测距的Compass定轨精度Tab.3 Orbit determination RMS3Dfrom satellite to satellite double directions ranging /cm

[1] RAN Chengqi.Plan of Compass Development[R]Beijing:Chinese Compass Satellite Navigation Systems Management Office,2010.(冉承其.北斗卫星导航系统发展计划[R].北京:中国第二代卫星导航系统专项管理办公室,2010.)

[2] SUN Jiadong.Evolution of Compass[R].Xi’an:Xidian University,2010.(孙家栋.北斗卫星导航发展之路[R].西安:西安电子科技大学,2010.)

[3] WEI Ziqing,GE Maorong.GPS relative positioning mathematical model[M].Beijing:Survey and Mapping Press,1998.(魏子卿,葛茂荣.GPS相对定位的数学模型[M].北京:测绘出版社,1998.)

[4] GENG Tao.Real-time Precise Orbit Determination Theory for Navigation Satellite and Its Experimental Application Based on Regional Reference Stations[D].Wuhan:Wuhan University,2009.(耿涛.基于区域基准站的导航卫星实时精密定轨理论及试验应用[D].武汉:武汉大学,2009.)

[5] RAJAN J A,ORR M,WANG P.On-orbit Validation of GPS IIR Autonomous Navigation[C]∥Proceedings of the 59th Annual Meeting of the Institute of Navigation and CIGTF 22nd Guidance Test Symposium.Albuquerque:[s.n.],2003:23-25.

[6] RAJAN J A,PETER B,HARRIS R.Modernizing GPS Autonomous Navigation with Anchor Capability[C]∥ION GPS/GNSS.Portland:[s.n.],2003:1534-1542.

[7] BERNSTEIN H,ANDOR B F,JAMES G H.GPS User Position Accuracy with Block IIR Autonomous Navigation[C]∥Proceeding of the ION GPS-93.Alexandria:Institue of Navigation,1993:1389-1399.

[8] LIU Wanke.Research and Simulation on Autonomous Orbit Determination and Combined Orbit Determination of Navigation Satellite[D].Wuhan:Wuhan University,2008.(刘万科.导航卫星自主定轨及星地联合定轨的方法研究和模拟计算[D].武汉:武汉大学,2008.)

[9] SVEHLA D,ROTHACHER M.Kinematic Positioning of LEO and GPS Satellites and IGS Stations on the Ground[J].Advances in Space Research,2005,36(3):376-381.

[10] ZHU S,MASSMANN Y F H,YU Y,et al.Satellite Antenna Phase Center Offsets and Scale Errors in GPS Solution[J].Journal ofGeodesy,2003,76(11-12):668-672.

[11] GENG Jianghui,SHI Chuang,ZHAO Qile,et al.GPS Precision Orbit Determination from Combined Ground and Space-borne Data[J].Geomatics and Information Science of Wuhan University,2007,32(10):906-909.(耿江辉,施闯,赵齐乐,等.联合地面和星载数据精密确定 GPS卫星轨道[J].武汉大学学报:信息科学版,2007,32(10):906-909.)

[12] SCHUTZB,TAPLEY B,GEORGE HB.Statistical Orbit Determination[M].New York:Academic Press,2004.

[13] SHI C,ZHAO Q,GE M,et al.Introduction to PANDA Software and the Latest Development for High Precision GNSS Data Processing and Application[C]∥IGS Analysis Center Workshop.Newcastle:[s.n.],2010.

(责任编辑:宋启凡)

Compass Precise Orbit Determination Based on Space-ground Monitoring Network

GENG Tao,LIU Jingnan,ZHAO Qile,SHI Chuang
Research Center of GNSS,Wuhan University,Wuhan 430079,China

A way of orbit determination based on inter-satellite cross-layer observations is proposed.It classifies satellite orbits into various layers by their heights and if a receiver is set in MEO satellite,observations can be

from GEO and IGSO.According to the satellite constellation of the Chinese Compass satellite navigation system,precise orbit determination is carried out with satellite-ground observations(SGO),on the combination of satellite-ground and inter-satellite cross-layer observations(CLO),and on the combination of satellite-ground and inter-satellite two-way ranging observations(TWRO)in the condition of regionally-distributed ground stations and global unevenly-distributed ground stations.The orbit results are assessed by satellite tracked arcs,position dilution of precision(PDOD),comparing the estimated orbits with the simulated reference orbits.The results show that with only 1 d SGOs from the seven regional stations in China,RMS3Dof GEOs,IGSOs and MEOs are respectively reduced from 6.1 m,1.3 m and 5.9 m to 1.0 m,0.8 m and 2.0 m when CLOs,where the beam angle of ranging equipment increases up to 41.25°,orbit accuracies are better than 20 cm when TWROs,where the beam angle increases up to 45°and systemic error is period term with 30 cm amplitude.

satellite-ground monitoring network;precise orbitdetermination;integrated orbitdetermination;PANDA;Compass

GENG Tao(1982—),male,PhD,majors in satellite geodesy and precise orbit determination.

P228

:A

国家863计划(2007AA120603);中央高校基本科研业务费专项资金;地球空间信息工程国家测绘局重点实验室经费(201029);湖北省自然科学基金(2010CDA069)

1001-1595(2011)S-0046-06

2011-01-31

修回日期:2011-03-20

耿涛(1982—),男,博士,研究方向为卫星大地测量及卫星精密定轨。

E-mail:gt_gengtao@whu.edu.cn