一种导航卫星中长期轨道预报方法

周建华,杨 龙,徐 波,谢廷峰

1.北京环球信息应用开发中心,北京100094;2.南京航空航天大学,江苏南京210016

一种导航卫星中长期轨道预报方法

周建华1,杨 龙1,徐 波2,谢廷峰1

1.北京环球信息应用开发中心,北京100094;2.南京航空航天大学,江苏南京210016

基于神经网络混合建模的思想提出一种针对导航卫星的中长期轨道预报方法,在原动力学模型的基础上引入神经网络模型作为补偿,从而获得新的预报模型。在训练过程中神经网络通过学习动力学模型轨道预报误差来掌握其变化规律,并在预报过程中为动力学模型预报提供补偿,以提高预报精度。对 GPS卫星动力学模型中长期预报误差的特点进行分析,然后根据所得结论提出混合模型的中长期(15 d以上)预报方案,最后通过对 GPS卫星的仿真试验证明混合模型的改进效果,结果表明新方法在15～40 d的预报上表现出很好的改进效果。

轨道预报;神经网络;动力学模型;混合建模

1 引 言

导航卫星的自主导航是提高卫星系统生存能力的一个重要手段,而轨道精度是衡量其性能优劣的重要指标。在解决导航星座自主定轨中涉及高精度的星历预报,提高预报精度对导航精度有着重要的意义。传统的动力学模型轨道预报方法通过考虑卫星空间运动中的各种动力学因素,外推出卫星的运动状态。动力学模型的精度直接影响预报精度,然而由于空间动力学环境的高度复杂性及卫星本身各种参数的不确定性,动力学模型的精度受到限制,预报精度提高比较困难。

通过在动力学模型中加入经验力的方法可以在短期内提高轨道预报精度。然而由于动力学模型的时变性和复杂性,经验力模型将在长期预报中逐渐失去精度优势,甚至发生错误。如文献[1]建立了针对 GPS卫星的光压模型,提高了 GPS卫星的定轨精度,然而随着预报弧段的增加,预报误差将剧烈地发散,不能用于中长期预报。同时这种光压模型的建立工作量大,结构参数不适用于其他卫星,因此导航星中长期预报的改进需要一种新的方法。

为减少动力学模型的不足对预报结果的影响,文献[2]通过采用切比雪夫多项式拟合CHAMP卫星轨道然后进行外推的方法,完成在GPS卫星失锁状态下保持定轨精度的目的,然而该方法外推时间只有50 s,应用范围有限。近年来,神经网络在时间序列预报领域的应用得到广泛关注,作为一种新兴的建模工具,其建模是一种自适应映射的过程,不作假设,理论比较合理,能避开未知因素的影响,并且在建模过程中对系统本身的结构、参数等信息没有特别要求,有较好的适用性。基于以上两点,在轨道预报中引入神经网络,以改进预报方法。

关于神经网络在轨道预报中应用的研究较少,文献[3]根据 GPS卫星星历的相关周期特性,以时间序列预报作为基础,利用神经网络建立预报模型,在没有任何动力学模型的情况下得到精度为一个星期数百米的预报结果。然而由于将卫星位置量直接作为神经网络的输出,神经网络的状态量动态范围大,限制了预报精度的提高。

将神经网络与动力学模型相结合组成混合预报模型,旨在改进导航卫星的中长期预报结果,其中神经网络通过学习卫星状态量与力模型轨道预报的误差之间的函数关系来掌握已知动力学模型的不足,在预报过程中为力模型预报进行补偿,在不改变原有力模型的基础上,充分利用已有信息提高预报精度。鉴于导航星轨道预报改进算法的现实需求以及 GPS卫星的星历精密已知,本文以GPS卫星为研究对象探讨混合模型对卫星轨道预报方法的改进。

2 基于动力学模型轨道预报误差的特点

神经网络的引入是要建立针对力模型的补偿模型,在混合模型中提供对力模型的预报误差的补偿。力模型轨道预报的误差形态影响神经网络的类型、结构、训练集选取以及混合模型的结构,因此这里有必要先对它进行分析。

(1)首先给出PRN号为31的卫星在2001-01-04日0时的卫星的轨道预报误差曲线,如图1所示,这里给出在 X轴方向的误差随时间变化,另外两个坐标分量上的误差与之类似。

图1 31号卫星在2001-01-04日的轨道预报误差Fig.1 Prediction error of PRN31 on 2001-01-04

由上图可知,在40 d的预报弧段内,前5～6 d的轨道预报误差保持在较小的范围以内,而在6 d以后预报误差发散严重。预报误差形态呈扩散态并且具有周期性,周期接近于卫星的绕行周期。

(2)力模型轨道预报的效果受多种因素的影响。而不同初始历元(轨道预报的开始时间)下的轨道预报误差大小有时往往会有很大的差别,为了更好地认识初始历元对预报误差的影响,这里以2001-01-04—2001-05-04每天的00:00:00时作为初始时刻,在此120个不同的初始时刻下分别进行40 d的轨道预报,图2中按照时间顺序分别给出此120个初始时刻下的位置预报误差。为了便于分析,这里将各个时刻的数值按时间顺序连成线,得到如图2的结果。

图2 31号星不同初始历元下预报40 d的误差大小Fig.2 40 d prediction error of PRN31 for deferent initial epoch

由上图可知,对于31号星在同一力模型下预报同样长度的弧段预报误差有很大的差异,40 d的预报最大值从几十米到上千米不等,120次试验的平均值为350 m。同时预报误差跟初始历元之间存在着一定的规律:变化随初始历元的选取具有周期性、连续性,观察可得相隔14 d的预报结果相近。

(3)对于特定的力模型而言,预报误差随不同的卫星而有所差异,下面给出 PRN3的卫星预报40 d的结果,如图3所示。

由上面的图形可知,对于不同的卫星轨道预报的误差变化及分布有所不同,但变化规律均可以总结为以下几点:①预报误差发散趋势会随着预报时间的延长而加剧;②预报误差变化跟卫星绕行周期有一定的关系;③预报误差的大小随着初始历元的不同而有很大的差异,同时又与初始历元之间有一种连续性、周期性的关系。

图3 3号星在不同初始历元下预报40 d的误差大小Fig.3 40 d prediction error of PRN3 for deferent initial epoch

3 混合模型的建立

在神经网络的实际应用中,其逼近模型的精度是有限的。如引言中所述,为减少神经网络所需逼近的范围,采用混合建模的方法,神经网络仅充当对动力学模型中不确定部分的补偿。基于这一思想构造了如图4和图5所示的混合模型。

图4 基于神经网络的混合模型结构图(训练阶段)Fig.4 The hybrid model structure based on neural network(training phase)

图5 基于神经网络的混合模型的结构图(预报阶段)Fig.5 The hybrid model structure based on neural network(predicting phase)

在图4中,IGS星历为 GPS卫星的精密星历,用作卫星实际位置信息以衡量动力学模型及混合模型的预报精度。动力学模型的预报星历X、V、T与其误差ΔX作为神经网络的训练样本,其中预报星历 X、V、T作为神经网络的输入,预报误差ΔX作为神经网络的理想输出。

在训练过程中神经网络逼近如式(1)所示的函数关系,经过训练的神经网络将在图5所示的预报过程中为动力学模型预报提供补偿,混合模型的预报星历、T的表达式为式(2)。

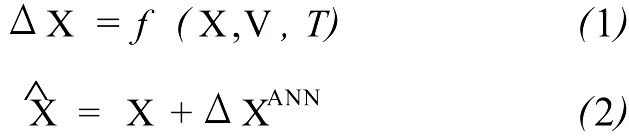
式中,预报初值 X0、V0、T0由 GAMIT软件计算获得,对两天观测资料的拟合精度优于0.05 m,接近IGS星历本身的精度,本文中可不考虑初值精度对预报误差的影响。动力学模型参考GAMIT软件,由于在仿真过程中发现Bernese光压模型在长期预报中的表现较差,因此这里选用长期预报较稳定的SRDYZ模型,其模型表达式参考文献[4]。

4 混合模型的预报方案

在正确的训练条件下,完成训练的神经网络具备一定的外推能力,可保证一定时间内输出的准确性。

由前面的讨论可知,对于 GPS卫星的动力学模型预报结果,10 d后的预报误差数值变化范围大,发散趋势难以精确把握,因此对于中长期预报(预报弧段大于15 d)无法采用直接外推的方法完成预报。尽管如此,根据第2节得到的特点(2)和特点(3),给出如下的预报方案:

(1)某初始时刻下的预报误差作为训练样本完成对神经网络的训练;

(2)利用训练完的神经网络在其他初始时刻下的预报结果提供补偿。

第2节中对 GPS卫星在不同时刻下的预报误差进行分析,得出相隔14 d时预报误差大小和相位均较接近,因此选择14 d(或其整数倍)之前的预报结果作为训练样本,得到的神经网络可对当前时刻下的预报星历进行补偿。

上述预报方案的具体实现如表1所示,其中由于 T1＜T0,因此训练弧段的长度最大为14 d,相应地能够在预报过程中提供的补偿弧段长度为14 d左右。如需延长补偿弧段,则要增长训练样本的时间跨度,具体方法是以 T0-28、T0-42作为训练的初始时刻。

其中

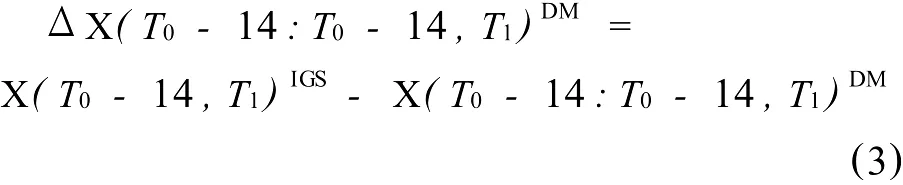
为方便表达,定义表达式 Z(a:b,c)model来表示某弧段内的相关信息,其中 Z为状态量的符号,model为计算该量所用的模型,a为初始历元时刻,b为弧段的开始时刻,c为该弧段的结束时刻;X、V分别为星历的位置、速度信息;ΔX是星历的位置误差量;T0为某一历元时刻;T0-14是离 T0距离14 d时的时刻;T1为训练弧段的截止时刻;T2为预报弧段的截至时刻。各量右上标中,DM为动力学模型;ANN为神经网络模型;HM为混合模型。

表1 中长期预报方案Tab.1 The middle and long duration prediction scheme

5 神经网络设计

在神经网络应用中为保证网络性能以完成预定任务,需要认真考虑训练集预处理、网络结构设定及训练算法等。这里网络的性能主要表现在训练效率及泛化能力,泛化能力是指辨识训练样本中所隐藏的规律,并且当被输入样本以外数据时,网络能正确地反映这种规律的能力。关于网络泛化能力的相关讨论及改进措施,文献[5]进行了翔实的总结,这里介绍本文中涉及的几种方法。

有时训练完的神经网络会对输入有较高的敏感性,即输入中的细小偏差会导致输出的极大不同,从而表现出很差的泛化能力。这时在训练样本中适当加入噪声可以使网络输出对网络的输入变化的敏感性逐渐减少[6]。

神经网络结构对网络的性能影响尤为重要,如何确定合适的结构是神经网络设计中的难点,结构太简单会导致网络“欠适配”,结构过于复杂则会导致网络“过适配”,一般的共识是在满足一定训练精度的基础上,网络结构越简单泛化能力越好。在实际应用中,可以根据先验信息在训练开始前确定,也可利用自裁剪算法在训练过程中动态确定,文献[7]介绍了一种较为可行的自裁剪算法,其基本思想是在训练过程中使对目标函数贡献较小的权值自动地衰减到零,从而达到精简网络结构的目的。根据 Kolmogorov定律确定初始隐层节点数,并在试验过程中根据结果不断调整,其准则为在满足一定训练精度的情况下,网络结构尽量简单。

在神经网络的训练过程中,目标函数正则化的方法是通过限制权值的范围来提高泛化能力的,此时目标函数的形式为

式中,Ed为神经网络输出量相对于理想输出误差的平方和;Ew为所有权值的平方和。

如式(6)和式(7)所示。式中,d为网络的理想输出;a为网络实际输出;β、α为正则化的权值。确定β、α的大小是求解正则化问题的关键,常规的正则化方法难以确定它们的大小,而贝叶斯正则化的方法可以在网络训练过程中自适应地对它们进行调整,使其达到最优。David Mackay在贝叶斯框架下,认为神经网络参数和训练集的先验概率服从正态分布,由后验概率最大化求解出β、α[8]

式中,M是样本中输出维数与样本数的乘积;γ用来表示训练样本中网络参数的有效个数,γ=n-2αtr(H)-1,n是网络中所有权值的个数,H是目标函数的 Hessian矩阵,其计算量很大,文献[9]中采用了 Gauss-Newton法来近似计算 Hessian矩阵,提高了运算效率。在MATLAB的神经网络工具箱中,训练函数trainbr()采用基于Levenberg-Marquardt的贝叶斯正则化方法,在训练过程中兼顾泛化能力。本文神经网络模型的训练过程由trainbr()函数完成。

6 仿真试验及结果

为了验证混合模型的改进效果,以 UTC 2001-01-05 T23:59:47.00时作为训练初始时刻 ,对 PRN31、PRN7、PRN6、PRN3、PRN27、PRN19分别进行中长期预报和长期预报试验,其中中长期预报的预报弧段为15 d,长期预报为30 d、40 d,长期预报的预报方案与中长期时的相似,只是在训练样本中注入了适当的随机误差。通过与IGS星历的比对得出混合模型的预报精度和动力学模型的预报精度,得到如下的仿真结果。

6.1 中长期预报仿真结果

根据中长期预报方案,以14 d前的预报信息作为训练样本,在下新初始时刻下进行预报,预报弧段为15 d,训练样本按30 min的间隔进行采样。对PRN31卫星,训练完成后 SS E=29,SSW=24,训量过程用时为20 s,混合模型及相应的动力学模型的预报误差如图6所示。由图6可以看出,虽然混合模型在前几天内的预报精度不高,但其误差发散趋势明显比动力学模型的缓慢,15 d的预报误差为45 m,而动力学模型预报误差为130 m,可见混合模型控制误差了发散趋势,改进效果明显。

图6 PRN31中长期预报中混合模型和动力学模型误差曲线(J2000地心惯性系下)Fig.6 The long duration prediction error curve of PRN31 when hybrid model and dynamic model used(J2000 inertial reference frame)

表2是混合模型和动力学模型的预报15 d的误差,通过对比可知混合模型在预报4 d时的改进效果不是很明显,对于 PRN31、PRN7、PRN6、PRN3 4颗卫星,其误差大小与动力学模型相近,然而在8 d时,混合模型的预报误差改进效果比较明显,对6颗卫星均有50%左右的改进效果,并且保持到了15 d。表2列出在中长期预报中混合模型对动力学模型的改进程度。

由表2可知,混合模型对6颗卫星都有一定的改进效果,除了PRN27卫星外其他5颗卫星的改进均优于60%,并且除“星蚀”卫星以外的其他5颗卫星预报误差均在 50 m以内。对于PRN19,由于发生了“星蚀”,动力学模型预报误差较大,达到了近400 m,因此在改进66%的情况下混合模型预报误差依然比其他卫星要大。

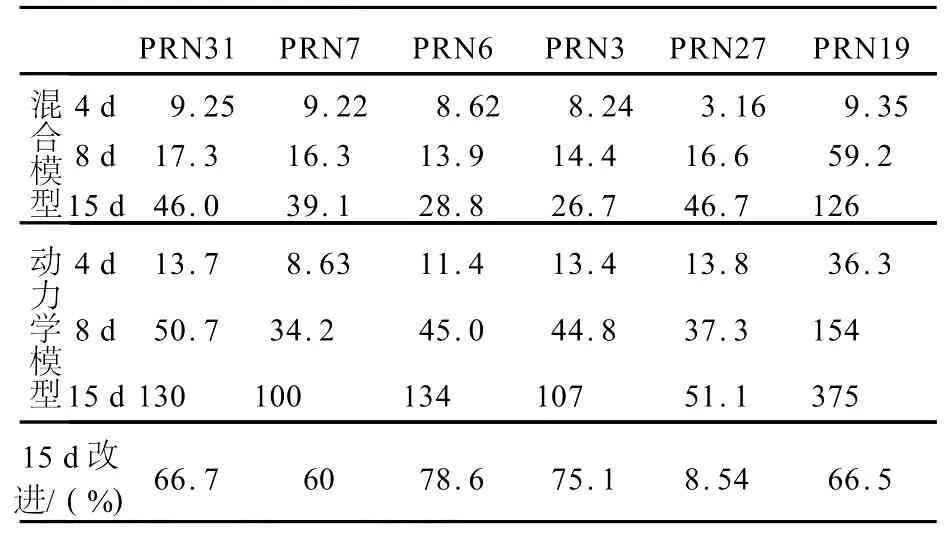
表2 混合模型和动力学模型对6颗卫星的中长期预报误差对比Tab.2 The comparison of prediction error between hybrid model and dynamic model for 6 satellites /m

6.2 长期预报仿真结果

根据中长期预报方案,为了实现30 d、40 d的预报,分别采用28 d、42 d之前的动力学模型预报结果作为训练样本,另外需在训练样本中注入适当噪声以提高网络的泛化能力。在仿真过程中发现,输入噪声的量级采用输入量的1%～5%时较为合适,利用MATLAB中rand函数获得。对于PRN31,混合模型及相应的动力学模型的预报误差如图7和图8所示,可以确定的是,以长度为28 d、42 d的预报结果作为训练样本使混合模型实现了在30 d、40 d长期预报中对误差发散趋势的控制。

图7 PRN31长期预报30 d混合模型和动力学模型误差曲线(J2000地心惯性系下)Fig.7 The 30 d prediction error curve of PRN31 when hybrid model and dynamic model used(J2000 inertial reference frame)

图8 PRN31长期预报40 d混合模型和动力学模型误差曲线(J2000地心惯性系下)Fig.8 The 40 d prediction error curve of PRN31 when hybrid model and dynamic model used(J2000 inertial reference frame)

表3 混合模型与动力学模型对6颗卫星的30 d预报误差对比Tab.3 The comparison of prediction error between hybridmodel and dynamic model for 6 satellites in 30 d/m

表3分别是混合模型和动力学模型预报30 d的误差,同时,表中列出了混合模型的改进程度。其中PRN6在预报第25 d进行了轨道机动,混合模型失去改进的作用。混合模型对其他卫星的改进效果明显,除发生“星蚀”的 PRN19外,均取得了50%左右的改进效果,PRN19的预报误差较大,改进效果不佳。

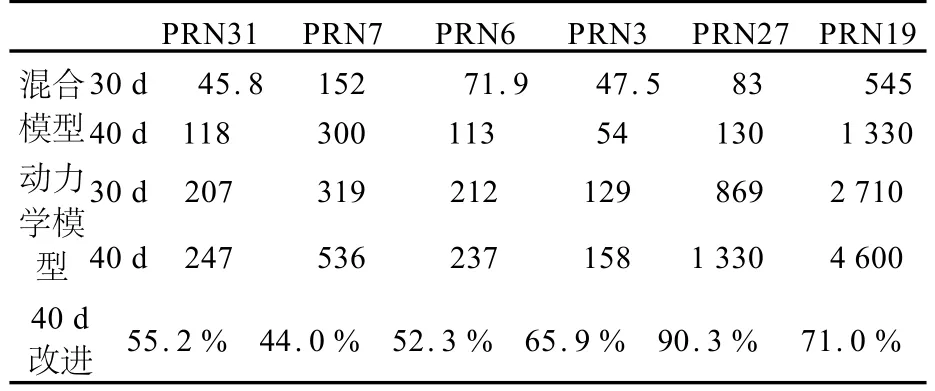
表4 混合模型与动力学模型对6颗卫星的40 d预报误差对比Tab.4 The comparison of prediction error between hybrid model and dynamic model for 6 satellites in 40 d/m

表4是预报40 d时两种模型的预报误差,PRN6的训练开始时刻选择了2001-02-04,这样可以避开轨道机动。对比表中数据,6颗卫星均取得了较理想的改进效果,表中列出预报40 d时混合模型的改进程度,可见改进效果在50%左右。

对于具体的预报过程,先采用短期预报方案保证前几天的预报精度,然后采用中长期预报方案对误差发散趋势进行控制,从而完成在整个弧段内的预报。

6.3 不同初始时刻下的仿真结果

对于任何预报模型,在不同的初始时刻下预报误差的形态都会有一定的差异。为了把握补偿方案的改进性能,需要研究其在不同初始时刻下的改进效果,为了方便与 IGS星历进行比较,选择2001-01月—2001-04月的100 d中每天的UTC 23:59:47时作为初始时刻,在各个时刻下进行预报记录混合模型的改进。

图9是 PRN31在100个初始时刻下混合模型的改进结果,可以发现混合模型虽然不能保证每次都能取得改进,但是却能保证预报误差整体比动力学模型要小,其中的柱状图中可见,混合模型的预报误差分布比动力学模型要集中,并且明显左移。

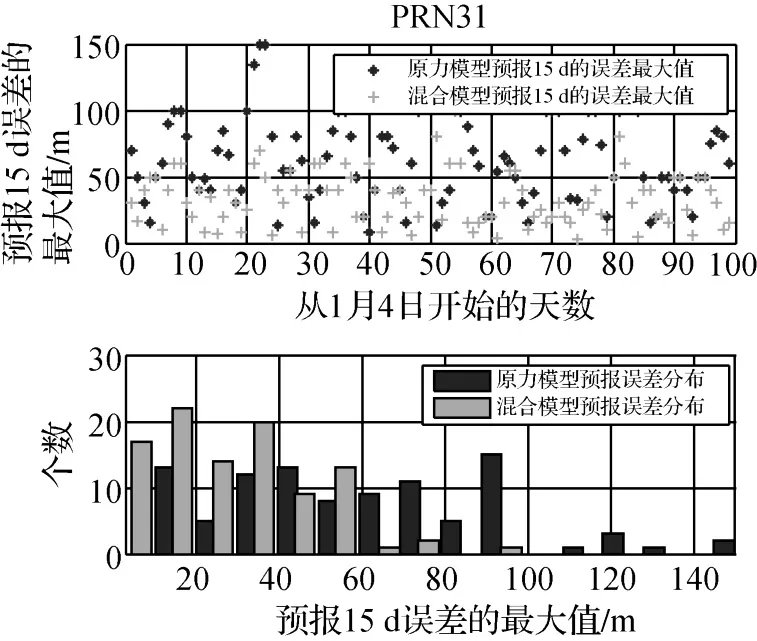
图9 PRN31在100个不同初始时刻下动力学模型和混合模型预报15 d的误差Fig.9 The 15 d prediction error of PRN31 when hybrid model and dynamic model used for deferent initial epoch

表5是 PRN31和 PRN3两颗卫星在100个初始时刻下,预报误差的统计结果。可见,对于PRN31、PRN3两颗卫星,混合模型在100个不同初始时刻下共有70次具有明显的改进效果,并且混合模型预报误差的平均值、标准差和最大值均比原动力学模型要小。改进效果在70%左右。

表5 PRN31和PRN3在100个不同初始时刻下两个模型预报15 d的误差统计Tab.5 The statistic of 15 d prediction error of PRN31 and PRN3 when hybrid model and dynamic model used for 100 deferent initial epoch

在100个不同初始时刻的统计结果说明尽管混合模型无法保证在每个初始时刻下都取得理想的改进效果,但其预报误差的均值更小,误差分布更集中。

7 结 论

基于神经网络混合建模的思想,根据动力学模型轨道预报误差的特点,完成中长期轨道预报方案的设计,通过仿真试验,证明混合模型的特点有:

(1)神经网络训练可以在1 min内完成,相对预报弧段的长度来说,可以做到实时预报。

(2)混合模型在中长期预报中能有效地控制预报误差的发散趋势,保证模型在长期预报中的改进。

(3)尽管混合模型无法保证在每个初始时刻下都取得理想的改进效果,但其预报误差的均值更小,误差分布更集中。

另外,虽以 GPS卫星作为研究对象,但由于神经网络的自适应学习能力,混合模型的方法在理论上完全可以推广到其他卫星,只是其他卫星的精密星历相关信息缺乏,需另外计算或者以其他信息代替。

[1] SPRINGER T A,BEUTLER G,ROTHACHER M.New Solar Radiation Pressure Model for GPS Satellites[J].GPS Solutions,1999,2(3):50-62.

[2] ZHAN G Ruwei,LIU Genyou.Study of L EO Satellite Orbit Fit and Prediction Method[J].Geodetic and Geodynamic,2008,28(4):115-120.(张如伟,刘根友.低轨卫星轨道拟合及预报方法研究[J].大地测量与地球动力学,2008,28(4):115-120.)

[3] LIU Tianlei.Estimate of GPS Satellite Orbit and Ephemeris with Quasi Neural Network and Polynomial Curve Fit[D].Taibei:Taiwan University of Science and Technology,2007.(刘添雷.应用类神经网路与多项式曲线拟合估测GPS卫星轨道与星历[D].台北:台湾科技大学,2007.)

[4] CHEN Junping.The Sun Radiation Model Used in GPS Watellite Orbit Determination[J].Astronomy,2006,47(3):310-319.(陈俊平.GPS定轨中的太阳辐射压模型[J].天文学报,2006,47(3):310-319.)

[5] WEI Haikun.The Functionality Ability and Functionality Method of Neural Network[J].Journal of Automatic,2007,27(6):806-813.(魏海坤.神经网络的泛化能力与泛化方法[J].自动化学报,2007,27(6):806-813.)

[6] MA TSUO KA K.Noise Injection into Inputs in Backpropagation Learning[J].IEEE Transactions on Systems,Man and Cybernetics,1992,22(3):436-440.

[7] ISHIKAWA M.Structural Learning with Forgetting[J].Neural Network,1996,9(3):509-521.

[8] MACKAY D J C.Bayesian Interpolation[J].Neural Computation,1992,4(3):415-447.

[9] FORESEE F D,HAGAN M T.Gauss-Newton Approximation to Bayesian Learning[C]∥Proceedings of the IEEE International Joint Conference on Neural Networks.Houston:[s.n.],1997:1930-1935.

(责任编辑:雷秀丽)

A Long Duration Orbit Prediction Method for Navigation Satellite

ZHOU Jianhua1,YANGLong1,XU Bo2,XIE Tingfeng1
1.Beijing Global Information Application and Development Center,Beijing 100094,China;2.Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China

A hybrid prediction model based on neural network is introduced for navigation satellite.The new model is based on dynamical model and the neural network model is adopted to modify it.During the training phase,neural network model tries to approach the difference of dynamical model prediction product,then compensate it in the prediction phase.The characteristics of DMM prediction error for GPS are explored,and then predition strategy for long term(longer than 15 d)is designed.At the last,a group of tests on GPS satellites are processed to prove and evaluate the performance of the new method,the test results show that the improvement for 15～40 d prediction is obvious.

orbit prediction;artificial neural network;dynamical model;hybrid model

ZHOU Jianhua(1962—),female,PhD,research fellow,majors in satellite navigation and precise orbit determination.

P228

:A

1001-1595(2011)S-0039-07

2011-01-28

修回日期:2011-03-22

周建华(1962—),女,博士,研究员,主要从事卫星导航与精密定轨技术研究。

E-mail:jianhua.zhou@yahoo.cn