凸截面注射成型全三维充填和纤维取向模拟研究
2011-11-04熊爱华柳和生黄兴元赖家美黄益宾
熊爱华,柳和生,黄兴元,罗 章,赖家美,黄益宾
凸截面注射成型全三维充填和纤维取向模拟研究
熊爱华1,2,柳和生1*,黄兴元1,罗 章1,赖家美1,黄益宾1,2
(1.南昌大学聚合物成型研究室,江西南昌330031;2.上饶师范学院物理与电子信息学院,江西上饶334001)
选用15%玻璃纤维增强聚酰胺6(PA6)复合材料,根据 Folgar-Tucker理论模型,研究了凸形截面零件全三维注射成型充填流动行为和纤维取向分布规律。结果表明,全三维模拟技术可以有效反映注射成型充填的流动形态和喷泉效应;凸形截面表层纤维沿剪切方向取向分布,且制品大端部分的纤维取向程度比小端部分差;3个坐标方向上的纤维取向分布非常复杂,沿x轴负方向(即充填方向),随充填长度的增加,纤维取向程度先增大后减小;沿y轴方向,随着距中心距离的增大,凸形截面小端部分的纤维取向程度由内向外逐渐增大,而大端部分的纤维取向程度先增大后减少;沿z轴方向,凸形截面小端部分的纤维取向由内向外呈增大趋势,大端部分的纤维取向程度却逐渐减小。
聚酰胺6;注射成型;凸形截面;模拟;充填;玻璃纤维;取向
Abstract:According to the Folgar-Tucker model,full 3D simulation of injection filling behavior and fiber orientations was studied for a sample of 15%short glass fiber reinforced polyamide 6 with a convex cross section.It showed that full 3D technology could simulate effectively filling behavior and the fountain effect of injection molding.The fiber orientation in the skin was parallel to shearing flow,and the degree of fiber orientation in the big end of the samples was lower than in the small end.The fiber orientation of 3D solid was complex along the three axes.In thexdirection,the degree of fiber orientation increased at first,then decreased with increasing filling length.Along theyaxis,the degree of fiber orientation in the small end increased gradually with increasing distance to the core,but the degree of fiber orientation in the big end increased at first then decreased.Along the direction ofzaxis,the degree of fiber orientation in the small end tended to increase from core to skin,while that was reducing gradually in the big end.
Key words:polyamide 6;injection molding;convex cross section;simulation;filling;glass fiber;orientation
0 前言
树脂基复合材料是现代复合材料的典型代表,已广泛应用于航空航天、电子电器、石油化工、建材、汽车、轮船、体育器材和生活用具等各个方面。注射成型是纤维增强树脂基复合材料成型加工的主要方法,成型制品的力学性能与加工过程中充填流动引起的纤维取向有关。目前国内外研究者大多数从实验与模拟两方面对之进行研究[1-4],其中成型过程中纤维取向分布预测的数值模拟研究对纤维复合材料的实际应用具有非常重要的意义。
目前被人们广泛采用的模拟方法主要是基于Hele-Shaw理论模型的薄壳分析理论,该理论通常采用中面模型或表面模型。Kech等[5]基于Folgar-Tucker模型通过实验和模拟对比研究了薄壳塑件注射成型纤维取向分布规律,但由于薄壳理论忽略了厚度方向的流动和熔体前沿的喷泉效应,因此不能有效描述三维流动区的流动行为,且随着制品复杂程度的增加,在选择模型的中面时存在较大的困难,所以全三维模拟技术已成为一种必然手段。Michaeli等[6-7]对注射成型过程进行了三维模拟,并采用着色粒子法进行跟踪观测,验证了三维模拟技术的有效性。Telmar等[8]对树脂传递模塑工艺成型圆管塑件的纤维取向进行三维研究,建立了纤维增强的理论模型,并用实验验证了模型的有效性。Lee等[9]采用有限元技术和耦合3D分析方法对纤维增强的聚对苯二甲酸丁二酯进行模拟研究,建立了等效体积单元 (RVE)刚度理论模型,耦合3D分析方法与实验结果比较吻合,且RVE模型预测的刚度值大于实际值。Bernasconi等[10]通过检测纤维取向的角度,模拟研究了壳层-芯层纤维的形貌。由于全三维模拟技术考虑了厚度方向的影响,使模型更贴合生产实际,尤其是对纤维取向研究更应采用全三维技术。但目前由于该技术计算量大、收敛性差、对设备要求较高等缺点,其应用受到一定的限制,国内外对这方面研究的报道较少。同时由于有限体积法与有限差分、有限元法相比更具优势且物理意义明确,在流体流动和传热问题求解中最为有效,应用越来越广泛。
本文基于Moldex 3D软件平台,采用3D实体模型进行注射成型充填阶段的全三维分析[11]。Moldex 3D的三维实体分析是采用有限体积法的基本思想,采用半隐式压力-速度耦合来求解Navier-Stokes方程[12]。根据Folgar-Tucker纤维取向理论模型,选用凸形截面(截面面积比1∶4)厚度为40 mm 的制品,对含15%短玻璃纤维(GF)增强聚酰胺6(PA6)的注射成型充填过程和纤维取向进行数值模拟研究,揭示充填流动与纤维取向的关系,期望对生产实际提供一定的指导。
1 数学模型
1.1 控制方程
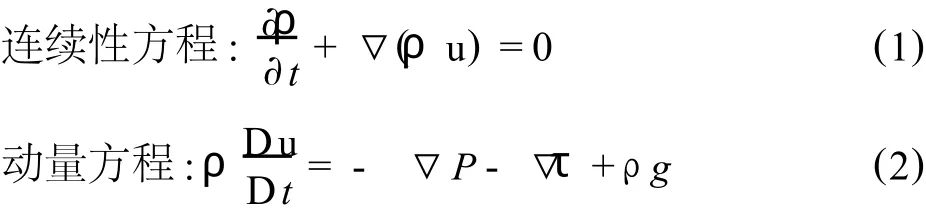

式中ρ——熔体密度,g/cm3
u——速度矢量,m/s
t——时间 ,s
P——压力 ,Pa
τ——偏应力张量,Pa
T——温度 ,K
CP——比热容 ,J/(kg·K)
k——热传导系数,m2·K/W
Φ——内部生成热,J
η——黏度,Pa·s ˙
γ——剪切速率,s-1˙
α——热转换率,%
ΔH——聚合释放的热量,J
1.2 纤维取向的定义
纤维取向的定义如图1所示,采用纤维取向向量P=P(θ,φ)和概率分布函数Ψ(θ,φ)定义某纤维取向在(θ,φ)和 (θ+dθ,φ+dφ)之间的概率 ,如式 (5)所示 ,但必须满足2个条件,如式(6)和式(7)所示。
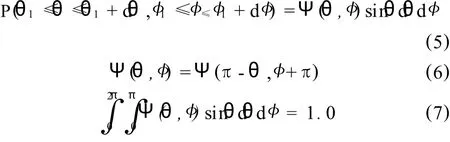
对于工程计算而言,求解概率函数Ψ(θ,φ)需要大量的计算时间,因而为了便于计算常采用二阶纤维取向张量 Aij表示,即:

因此,根据二阶取向张量的定义,可得到张量 Aij为对称张量,即:
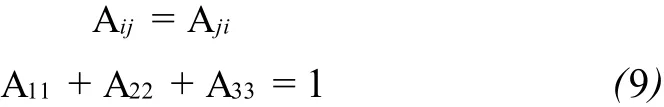
由于纤维取向张量为对称实数,它有3个正交特征向量 e1、e2和 e3及对应的特征值λ1、λ2和λ3,且每个特征值都介于0和1之间。
1.3 黏度模型


图1 纤维取向的定义Fig.1 Definition of oriented fibers
式中A1、2、D1、D2、D3、τ*——模型参数
η0——零剪切黏度,Pa·s
n——幂律指数
1.4 本构方程
本文拟采用 White-Metzner本构方程,如式(14)所示。

式中λ——松弛时间,s
1.5 数值方法
本文先通过Pro/E建模,保存为.stl文件后,采用3D实体进行网格划分,保证良好的网格质量,严格控制网格的长径比、扭曲度和正交度。采用流体体积(VOF)法实现熔体前沿界面追踪,设流体在计算网格内的体积函数为αq(x,y,z,t),αq∈[0,1],将体积函数看成是固结在流体质点上且随流体质点一起运动、没有质量和黏性的着色点。当αq=0时,表示该控制体积内无第q相流体;当αq=1时,表示该控制体积内全充满第q相流体;当0<αq<1时,则表示该控制体积内既包含第q相流体又包含了其他流体,视为熔体流动前沿,流体函数的输送方程和流体运动控制方程一起构成了VOF模型的控制方程。
2 数值算例
本文数值模拟算例选用塑件的几何构型为凸形截面,其实体和网格模型如图2所示,网格数为60608,网格节点数为65136,采用15%的短玻璃纤维增强PA6材料,选用修正 Cross模型,各参数的值为:n=0.23,D1=3.16e+18 g/(cm·s),D2=321 K,D3=0,A1=42.6,A~2=51.6 K。黏度与剪切速率的关系如图3所示。注射成型工艺参数为塑料温度T=265℃,充填时间tf=9.956 s。

图2 凸形截面构型实体模型的网格划分Fig.2 Solid geometry-mesh model of convex cross section of the part

图3 PA6/玻璃纤维复合材料的黏度与剪切速率关系曲线Fig.3 Curves for viscosity of PA6/glass fiber composites versus shear rate
3 结果与讨论
3.1 全三维充填行为分析
注射成型充填流动过程是一个非常复杂的物理过程。通常情况下,塑化良好的非牛顿熔体在柱塞或螺杆推压力的作用下由料筒前端经喷嘴、浇口、流道等向较低温度的型腔充填。在这极短的充填阶段,熔体要经历非常复杂的变化过程,一方面熔体由于模具传热而快速冷却,另一方面因高速剪切产生热量,同时伴随有熔体固化、体积收缩、分子取向及结晶等,其次熔体的流动前沿由于受到剪切和拉伸的共同作用,还会产生所谓的喷泉现象。从图4和图5可以看出,以充填时间所占比例为依据,在充填的初始阶段有明显的喷泉效应,之后的充填过程相对稳定,熔体前沿流动呈抛物线状,随着充填时间的延长和充填体积的增加,抛物线的弯曲程度发生变化,熔体前沿逐渐变得平坦,在凸形截面的小端部分形成稳定的充填流动,如图4(d)所示。当充填时间为整个充填时间的25%时,凸形截面的小端部分已充填完全,熔体进入凸形截面的大端部分,其充填流动行为与小端部分基本相似,只是由于凸形截面的小端部分与大端部分的面积比为1∶4,在截面突变和塑件的尖角处充填流动的速度有所变化,同时由于采用点浇口的形式,浇口区主要是扩散流动形式。

图4 凸形截面注射成型三维充填过程Fig.4 The 3D filling process of injection molded part with convex cross section

图5 凸形截面注射成型全三维充填结果Fig.5 The full 3D filling result of injection molded part with convex cross section
3.2全三维纤维取向分析
注射成型充填流动行为对纤维的取向有非常重要的影响。在充填过程中,纤维取向的整体变化趋势如图6所示。塑件的外表层与模具内壁接触,冷却速度较快,且受到壁面不同强度的剪切力作用,使得表层纤维的取向不尽相同,但总体上与充填剪切流动的方向一致,且凸形截面小端部分外表层的纤维取向性明显高于大端部分外表层的纤维取向,如图7所示,其主要原因是由于小端部分的塑料熔体冷却速度较快,受到流动剪切力作用较大,纤维沿流动方向取向且取向性较高。

图6 充填阶段纤维的取向分布Fig.6 Oriented fiber distribution during filling of injection molding
为了进一步研究内层熔体的纤维取向分布规律,本文分别沿3个坐标方向不同位置依次选取剖截面,如图8~10所示。需要说明的是由于在z轴和y轴方向的对称性,故在选取剖截面时分别从半厚宽和半高宽方向选取,即分别从三维制品的最前面(z=40 mm)向中心层方向(z=20 mm)及从最高上表面(y=40 mm)向中心层方向(y=0 mm)截取剖面。
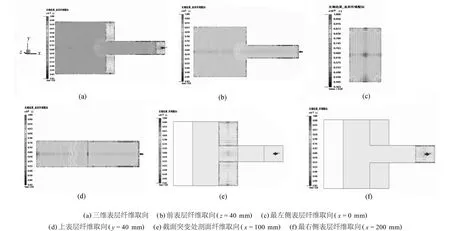
图7 三维表层纤维取向图Fig.7 3D diagram of oriented fibers in the skin
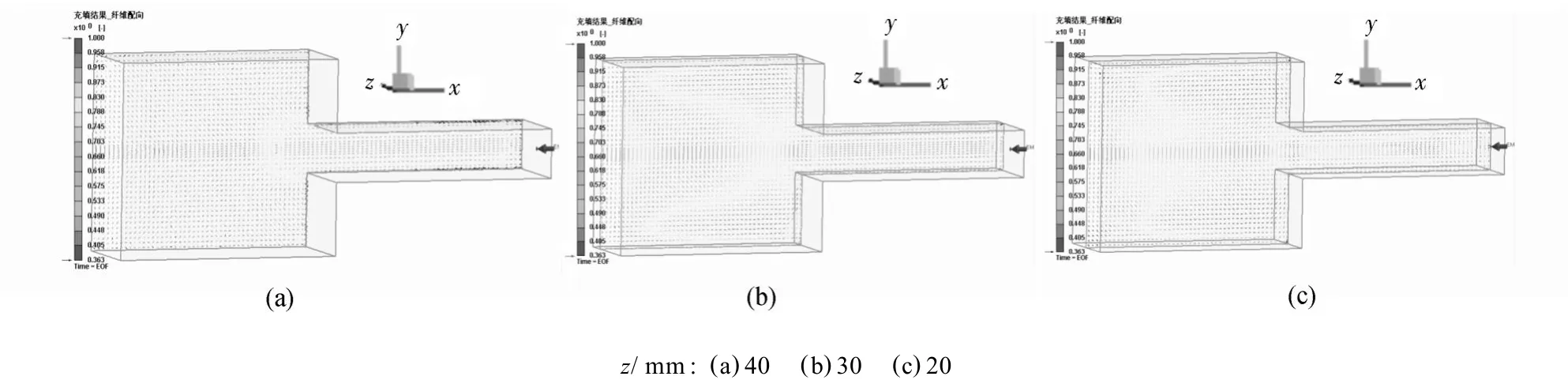
图8 沿z轴不同位置截面处的纤维取向分布Fig.8 Oriented fiber distribution at different cross sections alongzaxis
从图8可以看出,凸形截面大端和小端部分的外表层与中心层的纤维取向性各不相同。对于外表层而言,由于小端部分熔体的冷却速度大,受到的剪切力大,故纤维取向性最好,如图8(a)所示;而小端中心层部分,由于产生较大的剪切热,有充足的解取向能量,故纤维的取向性相对小端外表层而言相对较差,如图8(c)所示;在小端外表层与中心层间的过渡层,纤维的取向性相对较好,如图8(b)所示。但大端部分外表层与中心层的纤维取向分布变化规律正好与小端部分的变化规律相反,其原因是由于大端部分外表层熔体温度较低,大分子来不及取向,故取向性最差,而大端部分中心层部分相对大端的外表层温度较高,纤维取向性较高。
沿x轴方向在三维立体的左右两表面间均匀截取11个剖截面,如图9所示。从图9可以看出,除了在突变截面的边角处纤维取向性较差,纤维取向随机分布外,其余位置的纤维取向性较高,且随着充填长度的增加,纤维取向性先增大后减小。
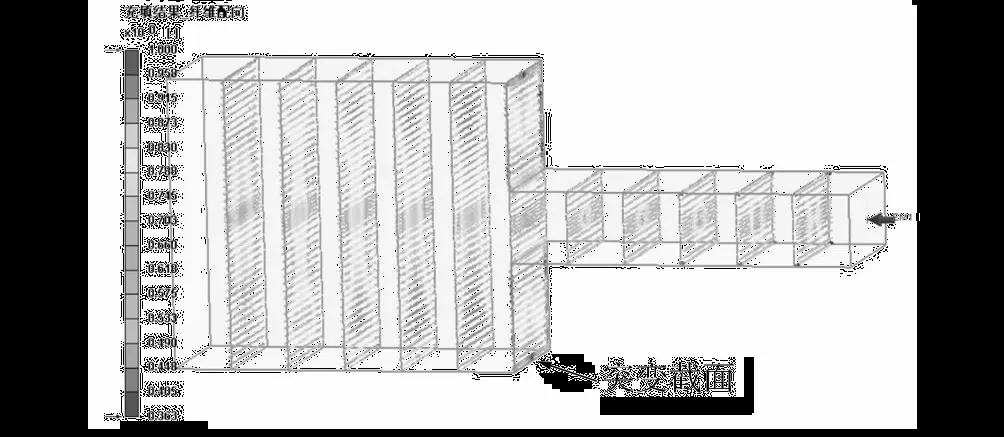
图9 沿x轴方向等距离位置截面处的纤维取向Fig.9 Oriented fiber distribution at different cross sections with equivalent distance alongxaxis
从图10可以看出,凸形截面大端的最高上表面(y=40 mm)的纤维取向性比小端的上表面(y=10 mm)的纤维取向性差。但沿y轴负方向不同位置剖截面的纤维取向性分布不尽相同。凸形截面大端部分最高上表面的纤维取向性最差,大端部分中心层的纤维取向性较差,而大端外表层和中心层间的过渡层的纤维取向性最好;凸形截面小端部分纤维的取向性则是外表层部分的最好,中心层部分的最差,且随着离中心层距离的增大,纤维的取向性逐渐提高。
由于纤维的取向分布不同,导致注射成型零件在三维空间产生的翘曲变形不同。从图11可以看出,沿流动方向(即x坐标负向)产生的翘曲变形位移最大,为0.950 mm,而沿厚度方向(即z方向)产生的翘曲变形最小,为0.141 mm,且流动方向主要产生负变形。

图10 沿y轴方向不同位置剖截面的纤维取向分布Fig.10 Oriented fiber distribution at different cross sections alongyaxis
4 结论
(1)通过对凸形截面塑件的注射成型充填阶段的全三维数值模拟,可以明显看出熔体的全三维充填流动过程和喷泉效应;
(2)凸形截面外表层纤维沿剪切方向取向分布,且大端部分的纤维取向性比小端部分的纤维取向性差;
(3)三维立体在3个坐标方向纤维取向分布各不相同。沿x轴负方向,随着充填长度的增加,纤维取向性先增大后减小;沿y轴方向,随着离中心距离的增加,凸形截面小端部分的纤维取向由内向外逐渐增大,而大端部分的纤维取向性先增大后减少。沿z轴方向,凸形截面小端部分的纤维取向由内向外呈增大趋势,而大端部分却逐渐减小;

图11 翘曲变形的位移分布Fig.11 Displacement distribution of warpage
(4)熔体的流动行为对纤维取向分布有影响,且最终影响制品的翘曲变形。
[1] Colin E,Ashley C.Fibre-orientation Measurements in Short-glass-fibre Compo-sites II:A Quantitative Error Estimate of the 2D Image Analysis Technique[J].Composites Science and Technology,2001,61(13):1961-1974.
[2] Colin E,Ashley C.Fibre-orientation Measurements in Short-glass-fibre Composites I:Automated, Highangular-resolution Measurement by Confocal Microscopy[J].Composites Science and Technology,2001,61(10):1389-1400.
[3] 上官林建,申长雨.短纤维复合材料注射成型纤维取向数值模拟研究进展[J].玻璃钢/复合材料,2009,(3):86-88.
[4] Zhou Kun,Lin Jianzhong.Research on 3D Fiber Orientation Distribution in Arbitrary Planar Flows[J].Journal of Zhejiang University Science A,2007,8(7):1021-1025.
[5] Kech A,Vincent M.Comparison Between Computed and Measured Fibre Orientation in Injection Moulded Parts[J].International Journal of Material Forming,2008,1(S1):747-750.
[6] Michaeli W,Kratz M,Stefan H.3D-flow Analysis by Means of Streamline Calculation[J].Macromolecular Materials and Engineering,2001,286(12):774-779.
[7] Michaeli W,Kratz M,Marx E.Development of a 3D-finite Element Module for the Prediction of the Fibre Orientation in Injection Moulded Parts[J].Macromolecular Materials and Engineering,2002,287(10):660-664.
[8] Telmar A,Agogu R,Soulat D.Prediction of Braid Deformability During RTM Process[J].International Journal of Material Forming,2010,3(S1):675-678.
[9] Lee D J,Kim M W,Kim S Y,et al.Three Dimensional Flow Simulation and Structural Analysis on Stiffness of Fiber Reinforced Anisotropic Parts[J].Korea-Australia Rheology Journal,2010,22(2):95-103.
[10] Bernasconi A,Cosmi F,Dreossi D.Local Anisotropy A-nalysis of Injection Moulded Fibre Reinforced Polymer Composites[J].Composites Science and Technology,2008,68:2574-2581.
[11] Core Tech System Co,Ltd.Moldex 3D R9.0 Reference Manual[CP].
[12] Chang S M,Jenn K K.Field Synergy Principle to Square and Trapezoid Types Fuel Cell Bipolar Plate of Mold Injection[C].Chengdu:Power and Energy Engineering Conference(APPEEC),2010:1-6.
Study on 3D Simulation for Filling Behavior and Fiber Orientations of Injection Molded Parts with Convex Cross Section
XION G Aihua1,2,LIU Hesheng1*,HUAN G Xingyuan1,LUO Zhang1,LAI Jiamei1,HUAN G Yibin1,2
(1.Polymer Processing Research Lab,Nanchang University,Nanchang 330031,China;2.School of Physics and Electronic Information,Shangrao Normal University,Shangrao 334001,China)
TQ320.66+2
B
1001-9278(2011)01-0083-07
2010-09-30
*联系人,hsliu@vip.163.com
