内压对薄壁铝合金管材充液压弯过程的影响

宋 鹏, 王小松, 徐永超, 苑世剑

(哈尔滨工业大学 材料科学与工程学院, 哈尔滨 150001)

内压对薄壁铝合金管材充液压弯过程的影响

宋 鹏, 王小松, 徐永超, 苑世剑

(哈尔滨工业大学 材料科学与工程学院, 哈尔滨 150001)

采用实验和数值模拟研究5A02铝合金薄壁管材充液压弯成形过程中内压对缺陷的影响规律，分析内压对弯曲内侧起皱、截面畸变及壁厚分布的影响，获得壁厚变化规律；通过数值模拟给出的应力状态，揭示缺陷形成机制。结果表明：提高内压能降低轴向压应力的绝对值，减小失稳起皱趋势，当内压超过一个临界值时，皱纹完全消除。对于直径为63 mm、壁厚为1 mm的5A02-O铝合金管材，其内压临界值为2.8 MPa。充液有效地减小截面畸变程度，随内压的增大，截面畸变程度逐渐减小。弯曲后，壁厚最大减薄点位于弯曲外侧点，且随内压的增大，轴向和环向拉应力均呈增大趋势, 弯曲外侧壁厚度减薄的趋势也增大。

内压；薄壁管；铝合金；充液压弯；起皱

薄壁铝合金弯曲管件在汽车、航空和航天等领域中有着广泛的应用，常用于汽车进气管件、车体结构件及航空航天各系统管路中[1−2]。相对于厚壁管件，薄壁(径厚比大于 50)管件弯曲成形中更易发生弯曲内侧管壁的起皱及弯曲外侧壁厚减薄甚至开裂等缺陷[3−4]。与钢相比，铝合金的伸长率低、塑性差，开裂倾向大；弹性模量仅为钢的1/3，起皱趋势严重。因此，薄壁铝合金管件弯曲成形更加困难。

为避免或减轻上述缺陷，在管坯内填料作为支撑是常用的方法。常见填充物有砂子、松香或低熔点合金等，但这些填充物不仅装填耗时，并且支撑内压不可控，还容易造成管坯内部损伤，弯曲质量较差[5−6]。为了解决这些问题，LOVRIC[2]提出充液弯曲方法。通过在管坯内部施加一定压力的液体介质作为支撑，降低起皱和截面畸变趋势，适用于二维变曲率轴线和薄壁管件的弯曲成形。

支撑内压是充液弯曲关键工艺参数之一。对低碳钢管材的三辊充液压弯研究表明：充液压弯与压弯相比，内侧起皱趋势明显减小；并且随内压的增大，截面畸变减小，外侧减薄率增大[7−8]。对不锈钢−碳钢双层复合弯头的充液压弯研究表明：提高内压，截面长轴长度变化不大，短轴长度提高较大，内层管的截面畸变得到有效控制；但如果内压过高，反而导致外层管外侧开裂[9]。

径厚比和相对弯曲半径是管材弯曲成形中用于确定工艺可行性及设备选择的两个重要参数，极限相对弯曲半径用于衡量一定径厚比管材的弯曲成形性能[10]。许多学者对不同径厚比时5A02-O铝合金管材CNC弯曲的相对弯曲半径进行研究，当径厚比为 47时，相对弯曲半径达到1.5[11]；当径厚比为50时，相对弯曲半径达到 2[12]。由一系列尺寸铝合金管材 CNC弯曲实验数据得到的经验公式计算出径厚比为 63时的极限相对弯曲半径为3.26。以上研究结果表明：径厚比越大，极限相对弯曲半径随之增大。此外，径厚比较大时，铝合金管材 CNC弯曲不仅受设备限制，而且极易出现外侧拉裂、内侧失稳起皱，表面划痕、夹痕等缺陷也难以控制，限制管材的弯曲成形极限。

相比之下，有关铝合金管材充液压弯的研究报道较少。有学者通过对5A02-O铝合金管材的三辊充液压弯实验研究得出：当径厚比为63时，极限相对弯曲半径为5[13]。通过对径厚比为63的AlMg3.0Mn铝合金管材充液压弯过程内侧起皱的分析，得到管材在不同相对弯曲半径时的内压临界值，随相对弯曲半径的减小，内压临界值增大；其中，当最小相对弯曲半径15.79时的内压临界值为2 MPa[14−15]。对弯曲半径较小时的研究尚未见报道。

本文作者采用实验和数值模拟方法，对径厚比为63的薄壁铝合金管材充液压弯成形进行研究，试件的相对弯曲半径为1.14。分析内压对弯曲内侧起皱、截面畸变及壁厚分布的影响，揭示内压对缺陷的影响规律。

1 管材充液压弯原理

图1所示为管材充液压弯基本原理。首先从管端充入液体，密封后形成一定的压力，然后在模具中进行弯曲，并随上模下压的过程控制管坯内的压力，利用液压的支撑作用避免起皱和截面畸变，在合模后，可提高内压进行整形，使管坯贴模定形。

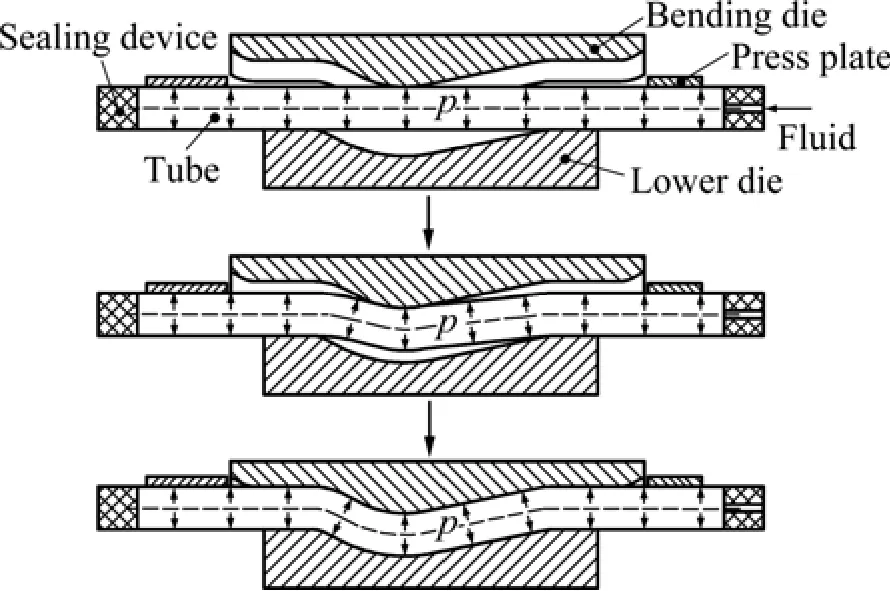
图1 充液压弯原理示意图Fig.1 Principle of hydro-bending

管坯在内压p的作用下，通过管端密封装置产生一定轴向拉应力，抵消内侧一部分压应力，有效地减小弯曲内侧发生起皱的趋势。对于一定弯曲半径，内压存在一个临界值，超过该值时，可以完全消除皱纹。

2 试件与材料

试件形状和尺寸如图2所示。试件轴线为三弯变曲率形状，左右不对称。管坯外径为63 mm，壁厚为1 mm，径厚比为 63。中间弯相对弯曲半径为2.86，弯曲角度为 39°；两侧弯相对弯曲半径均为 1.14，弯曲角度分别为27°和12°。两侧弯与中间弯之间均为直段，直段长度分别为25 mm和172 mm。

采用不圆度来描述截面畸变程度R，定义为

式中：dmax为截面长轴长度；dmin为截面短轴长度；d0为管坯初始直径。

图2 试件形状示意图Fig.2 Schematic diagram of specimen shape (mm)

实验中，选取试件中间截面测量几何尺寸和壁厚，典型壁厚测点为内侧点A和外侧点B。

实验所用材料为5A02-O铝合金管材，假定材料遵循指数硬化规律：

式中：i为流动应力；i为等效应变；n为硬化指数；K为强化系数。

经沿管材轴向切取弧形拉伸试样在英国INSTRON 5569R电子万能材料试验机进行单向拉伸试验，测得n=0.24，K=343 MPa，屈服强度sσ=80 MPa，均匀伸长率为14.6%。

3 初始内压及整形内压计算

3.1 初始内压

由于管坯两端密封，在充液压弯初始阶段，假设管坯的受力情况相当于承受内压作用的封闭薄壁筒，由Tresca屈服准则得管坯初始屈服时的内压ps为

式中：t为管坯壁厚；r为管坯半径。

3.2 整形内压

假设充液压弯后期的受力情况近似于内压作用下的环壳，弯曲区的应力状态如图3所示。由角度θ所限定的部分壳体内力垂直方向平衡条件和壳体的一般平衡方程，可以推导出轴向应力z和环向应力θ分别为

式中：p为内压；Rb为弯曲半径；r′为环壳上任一点到对称轴的距离。

从式(4)和(5)得到的环壳应力分布可以看出，当内压一定时，轴向应力z为一常量，环向应力θ在外环侧c点达到最小值。

c点的屈服内压为整个环壳的整形内压。由试件的几何尺寸，根据式(6)得到的试件整形内压为 2.74 MPa。

图3 环壳的应力分布Fig.3 Stress distribution of toroidal shell: (a) Stress state in bending zone; (b) Stress distribution

4 实验

4.1 实验方案

为了研究内压对弯曲的影响，根据上述内压理论计算，实验选取内压分别为 2.2、2.4、2.6、2.8、3.0和3.2 MPa。成形过程中内压保持恒定。

相关性检验结果表明，在油菜叶片和冠层图像集中，算法FIE的优势较为明显，各类算法中效果最好，表明油菜叶片表面上的主叶脉对油菜叶片氮营养诊断会产生一定的影响。

4.2 内压对起皱的影响

图4所示为实验得到的不同内压下弯曲内侧的起皱情况。由图4可以看出，试件的皱纹不是位于弯曲内侧圆弧的最低点，而是位于弯曲内侧圆弧靠近长直段一侧。这是由于右侧弯与中间弯之间的直段较长，右侧弯外侧轴向所受拉应力很难传递到中间弯内侧，对其轴向压应力的影响小。当内压小于2.8 MPa时，中间弯内侧圆弧靠近长直段一侧起皱；而当内压等于或大于2.8 MPa时，中间弯内侧圆弧两侧均无皱，可以获得合格试件。该值稍大于理论值，这是由于理论值未考虑材料硬化。当内压等于或大于3.2 MPa时，在弯曲过程中试件发生塑性变形，造成直径增大，导致试件在分模面处压出飞边，如图5所示。

图6所示为弯曲内侧皱纹尺寸测量示意图。其中皱纹深度h是指两皱峰与皱谷之间的垂直距离，皱纹实验得到的不同内压下的皱纹尺寸。由表1可以看出，宽度d是指皱纹沿试件环向的水平距离。表1所列为随内压的增大，皱纹的深度和宽度均逐渐减小，当内压等于或大于2.8 MPa时，皱纹完全消除。

图4 不同内压下弯曲内侧起皱情况Fig.4 Wrinkling on inner arc at different internal pressures: (a)2.2 MPa; (b) 2.4 MPa; (c) 2.6 MPa; (d) 2.8 MPa; (e) 3.0 MPa;(f) 3.2 MPa

图5 内压为3.2 MPa时分模面处飞边Fig.5 Burr along die parting face at internal pressure of 3.2 MPa

图6 皱纹尺寸测量示意图Fig.6 Schematic diagram of dimensions of wrinkles

表1 不同内压下皱纹尺寸的实验结果Table 1 Results of wrinkles dimensions at different internal pressures

4.3 内压对截面畸变的影响

图7所示为实验得到的中间截面不圆度与内压的关系。由图7可以看出，随内压的增大，截面畸变程度逐渐减小。当内压达到 2.8 MPa时，不圆度仅为1.37%，可以认为近似为圆形，说明充液能有效地减小截面畸变程度。

图7 不圆度与内压的关系Fig.7 Relationship between non-circularity and internal pressure

4.4 壁厚分布规律及内压的影响

壁厚测量选取内压等于或大于2.8 MPa时的3个合格试件。图8所示为实验得到的内压为2.8 MPa时的合格试件，其内侧与外侧沿轴向的壁厚分布如图 9所示。由图8和9可以看出，3个弯的内侧壁厚均增加，而外侧壁厚均减薄，壁厚最大减薄点位于中间截面的外侧点 B，最小壁厚为 0.893 mm，减薄率为10.7%。

图10所示为实验得到的内压为2.8 MPa时中间截面的环向壁厚分布。由图10可以看出，壁厚沿内侧点A到外侧点 B呈现下降趋势，在中性层以上(0°~90°)壁厚增厚，最大增厚率(A点)为5.8%；在中性层以下(90°~180°)壁厚减薄，最大减薄率(B点)为10.7%。

图8 内压为2.8 MPa时的合格试件Fig.8 Final sample at internal pressure of 2.8 MPa

图9 内压为2.8 MPa时的轴向壁厚分布Fig.9 Wall thickness distribution along axis at internal pressure of 2.8 MPa

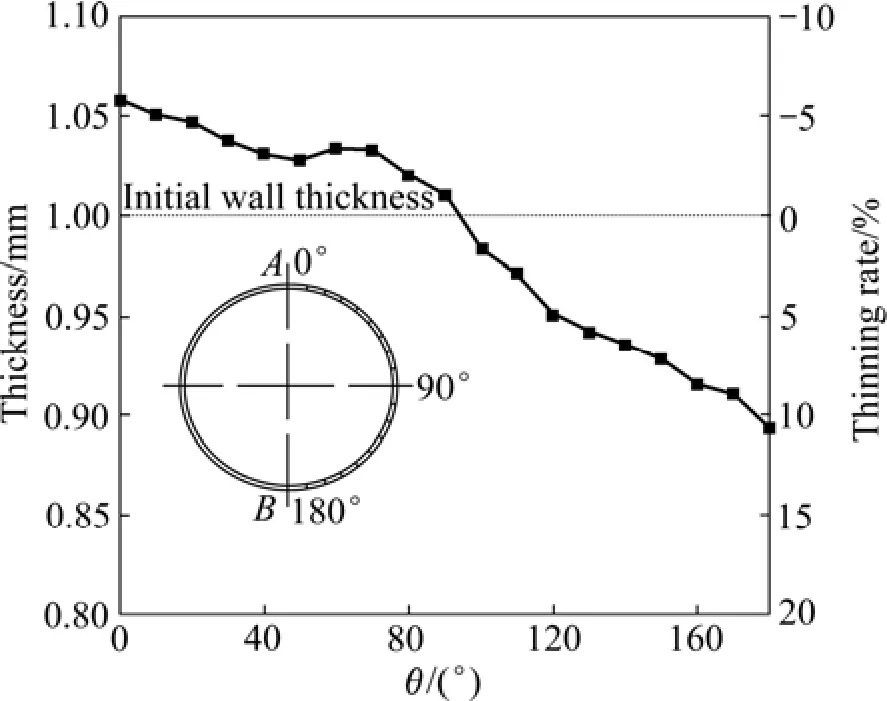
图10 内压为2.8 MPa时中间截面的环向壁厚分布Fig.10 Wall thickness distribution of middle cross-section at internal pressure of 2.8 MPa

内压对中间截面典型点A和B处壁厚的影响如图11所示。由图11可以看出，随内压的增大，内侧A点的增厚趋势减小，增厚率由 5.8%减小到 3.5%；外侧 B点的减薄趋势增大，减薄率由 10.7%增大到14.3%。较高内压下，外侧 B点壁厚明显减薄，弯曲外侧开裂的可能性增大。

图11 典型点壁厚与内压的关系Fig.11 Relationship between wall thickness at typical points and internal pressure

5 应力状态与缺陷形成机制

5.1 数值模拟模型

为深入分析缺陷形成机制，对充液压弯成形过程进行了数值模拟。所用软件为eta/DYNAFORM 5.6，求解器为LS−DYNA 971，数值模拟模型如图12所示。选用Barlat材料模型，材料力学性能参数根据拉伸试验结果选取。管坯划分为BT壳单元，模具和压板划分为刚性单元。摩擦选用Coulomb公式，摩擦因数选取0.05。内压通过沿管坯内壁的均布压力边界条件进行施加，内压选取与实验相同。

图12 数值模拟模型Fig.12 Numerical simulation model

5.2 弯曲内侧应力状态与起皱机制

成形过程中由内压引起的厚向应力较小，认为管坯的应力状态接近于平面应力状态。将内压为2.2 MPa时中间弯内侧皱谷处的节点在起皱前的应力数值与内压为2.8 MPa时同一节点在同一时刻的应力数值进行对比。图13所示为不同内压下皱谷节点的应力状态。由图13可以看出，该点均处于环向受拉、轴向受压的状态，但数值上发生了变化。当内压为2.2 MPa时，轴向压应力为−148.5 MPa；而当内压为2.8 MPa时，轴向压应力为−102.7 MPa，轴向压应力的绝对值明显降低。因此，提高内压能降低轴向压应力绝对值，减小失稳起皱趋势，有效避免弯曲内侧起皱的产生。

图13 不同内压下皱谷节点的应力状态Fig.13 Stress state at bottom of wrinkles at different internal pressures: (a) 2.2 MPa; (b) 2.8 MPa

5.3 弯曲外侧应力状态与开裂机制

图14所示为内压为2.8 MPa和3.2 MPa下相对压下量为85%时外侧点的应力状态。由图14可以看出，外侧点处于轴向和环向双拉的应力状态，并且轴向应力大于环向应力。随内压的增大，两个方向上的拉应力均呈增大趋势，由于轴向拉应力过大，弯曲外侧沿环向很容易发生开裂现象。

图14 不同内压下外侧点的应力状态Fig.14 Stress state at bottom of outer arc at different internal pressures: (a) 2.8 MPa; (b) 3.2 MPa

6 结论

1) 内压对充液压弯成形起皱影响显著，提高内压能降低轴向压应力绝对值，减小失稳起皱趋势，弯曲内侧皱纹的深度和宽度均逐渐减小，当内压超过一个临界值时，皱纹完全消除。

2) 对于直径为63 mm、壁厚为1 mm的5A02-O铝合金管材，当相对弯曲半径为1.14时，内压临界值为2.8 MPa。

3) 充液能有效地减小截面畸变程度，随内压的增大，截面畸变程度逐渐减小。当内压为2.8 MPa时，不圆度仅为1.37%。

4) 弯曲后壁厚最大减薄点位于弯曲外侧点，随内压的增大，轴向和环向拉应力均呈增大趋势，弯曲外侧壁厚减薄趋势增大。当内压为2.8 MPa时，最小壁厚为0.893 mm，减薄率为10.7%。

REFERENCES

[1] SCHUSTER C, LORETZ C, KLASS F, SEIFERT M. Potentials and limits with hydroforming of aluminium alloys[C]//Proceedings of the 4th International Conference on Hydroforming. Fellbach: MAT INFO, 2005: 113−135.

[2] LOVRIC M. Press-bending of thin-walled tubes/Increasing the productivity of internal high pressure forming processes[C]//Proceedings of the 4th International Conference on Hydroforming. Fellbach: MAT INFO, 2005: 365−386.

[3] PEEK R. Wrinkle of tubes in bending from finite strain three-dimensional continuum theory[J]. International Journal of Solids and Structures, 2002, 39: 709−723.

[4] 詹 梅, 杨 合, 江志强. 管材弯曲成形的国内外研究现状及发展趋势[J]. 机械科学与技术, 2004, 23(12): 1509−1514.ZHAN Mei, YANG He, JIANG Zhi-qiang. State of the art of research on tube bending process[J]. Mechanical Science and Technology, 2004, 23(12): 1509−1514.

[5] VOLLERTSEN F, SPRENGER A, KRRAUS J, ARNET H.Extrusion, channel, and profile bending: A review[J]. Journal of Materials Processing Technology, 1997, 87: 1−27.

[6] 赵长喜. 低熔点合金在复杂薄壁零件制造中的应用研究[J].航天制造技术, 2006(2): 15−18.ZHAO Chang-xi. Application of low melting point alloys to manufacturing of complex thin-walled parts[J]. Aerospace Manufacturing Technology, 2006(2): 15−18.

[7] 刘泽宇. 薄壁管的充液压弯成形研究[D]. 哈尔滨: 哈尔滨工业大学, 2007.LIU Ze-yu. Press-bending of the thin-walled tube with internal pressure[D]. Harbin: Harbin Institute of Technology, 2007.

[8] 刘泽宇, 滕步刚, 苑世剑. 内压对薄壁管充液压弯时的影响[J]. 塑性工程学报, 2009, 16(4): 35−38.LIU Ze-yu, TENG Bu-gang, YUAN Shi-jian. Effect of internal pressure on thin-walled tubes bending with internal pressure[J].Journal of Plasticity Engineering, 2009, 16(4): 35−38.

[9] 戴宇昕. 不锈钢−碳钢双层复合弯头充液成形研究[D]. 哈尔滨: 哈尔滨工业大学, 2009.DAI Yu-xin. Research on hydroforming of double-layer cladding elbow composed of stainless steel and low-carbon steel[D].Harbin: Harbin Institute of Technology, 2009.

[10] SHR Shiuan-guang. Bending of tubes for hydroforming: A state-of-the-art review and analysis[D]. Columbus: The Ohio State University, 1998.

[11] 申世军, 杨 合, 詹 梅, 李 成, 李 恒, 李海峰. 铝合金大口径薄壁管数控弯曲实验研究[J]. 塑性工程学报, 2007,14(6): 78−82.SHEN Shi-jun, YANG He, ZHAN Mei, LI Cheng, LI Heng, LI Hai-feng. Experimental study on large diameter and thin-walled aluminum tube NC bending process[J]. Journal of Plasticity Engineering, 2007, 14(6): 78−82.

[12] 寇永乐. 铝合金薄壁管小弯曲半径数控弯曲成形的实验研究[D]. 西安: 西北工业大学, 2007.KOU Yong-le. Experimental research on NC bending with small bending radius of aluminum alloy thin-walled tube[D]. Xi’an:Northwestern Polytechnical University, 2007.

[13] 李秋强. 薄壁管充液压弯的数值模拟和实验研究[D]. 哈尔滨:哈尔滨工业大学, 2009.LI Qiu-qiang. Numerical simulation and experimental research of thin-walled tube press-bending with internal pressure[D].Harbin: Harbin Institute of Technology, 2009.

[14] LIEWALD M, WAGNER S. State-of-the-art of hydroforming tubes and sheets in Europe[C]//Tube Hydroforming Technology:Proceedings of TUBEHYDRO 2007. Harbin: Harbin Institute of Technology Press, 2007: 19−26.

[15] LIEWALD M. Main research and current developments in hydroforming at the institute for metal forming technology(IFU)[C]//Proceedings of the 5th International Conference on Hydroforming of Sheets, Tubes and Profiles. Fellbach: MAT INFO, 2008: 111−130.

Influence of internal pressure on hydro-bending of thin-walled aluminum alloy tube

SONG Peng, WANG Xiao-song, XU Yong-chao, YUAN Shi-jian
(School of Materials Science and Engineering, Harbin Institute of Technology, Harbin 150001, China)

The influence of internal pressure on faults was investigated for a 5A02 aluminum alloy thin-walled tube in hydro-bending process by experiment and finite element method. The effects of internal pressure on wrinkling on the inner arc, cross-section distortion and wall thickness distribution were analyzed, and the thickness variation regularity was achieved. The mechanism of defect was revealed through stress state given by numerical simulation. The results show that the absolute value of axial compressive stress can be reduced by improving the internal pressure, and the wrinkling tendency declines. The wrinkles can be completely eliminated while the internal pressure reaches a critical value, and the critical value is 2.8 MPa for a 5A02-O aluminum alloy tube with an outer diameter of 63 mm and a wall thickness of 1 mm. The cross-section distortion decreases with the internal pressure increasing. The biggest thickness thinning of the specimen appears at the bottom of the outer arc. The axial stress and hoop stress enhance as the internal pressure rises, and the tendency of thickness thinning on the outer arc increases.

internal pressure; thin-walled tube; aluminum alloy; hydro-bending; wrinkling

TG394

A

1004-0609(2011)02-0311-07

国家自然科学基金资助项目(50875060)

2010-03-09；

2010-06-01

王小松，副教授，博士；电话：0451-86415754；E-mail: hitxswang@hit.edu.cn

(编辑 李艳红)