Cu-Cr纳米金属多层膜屈服强度/硬度的尺寸依赖性
2011-11-03张金钰牛佳佳雷诗莹
张金钰, 牛佳佳, 张 欣, 雷诗莹, 张 鹏, 刘 刚, 孙 军
(西安交通大学 金属材料强度国家重点实验室,西安 710049)
Cu-Cr纳米金属多层膜屈服强度/硬度的尺寸依赖性
张金钰, 牛佳佳, 张 欣, 雷诗莹, 张 鹏, 刘 刚, 孙 军
(西安交通大学 金属材料强度国家重点实验室,西安 710049)
采用磁控溅射方法分别在聚酰亚胺基体以及单晶硅基体上制备恒定调制比(η)以及恒定调制周期(λ)的Cu-Cr纳米金属多层膜;通过单轴拉伸试验以及纳米压痕试验系统研究Cu-Cr多层膜屈服强度及硬度的尺度依赖性。微观分析结果表明:基体对多层膜的微观结构无影响,Cu-Cr多层膜在生长方向上均呈现 Kurdjumov-Sachs取向关系,即{111}Cu//{110}Cr和〈110〉Cu//〈111〉Cr。力学测试结果表明:调制比恒定的Cu-Cr多层膜的屈服强度及硬度随调制周期的缩短而增加;调制周期恒定的Cu-Cr多层膜的屈服强度/硬度随调制比的增加而增加。Cu-Cr多层膜变形机制在临界调制周期(λc≈25 nm)和临界调制比(ηc≈1)由Cu层内单根位错滑移转变为负载效应。
纳米金属多层膜;强度;硬度;调制周期;调制比
由两种或两种以上的组元材料以相同或不同的单层厚度交替叠加组成纳米金属多层膜,可作为一种先进的工程材料,由于其独特的力学性能(如高强度/硬度)而广泛应用于微电子和微机械等高新技术领域[1−3]。作为高性能微电子器件及互连结构的核心材料体系,纳米金属多层膜在复杂的微加工制备和随后的服役过程中经常承受拉伸及循环载荷的作用,其变形损伤是导致系统失效的关键因素。因此,纳米金属多层膜的服役特性是当前的研究热点。目前,纳米金属多层膜的力学性能参量——硬度,主要是通过纳米压痕试验[4−9]测试获得,相应的研究结果整体表现出“越小越强”的趋势,即调制周期(或单层厚度)越小,多层膜的强度/硬度越高[4−9]。然而,通过单轴拉伸实验研究纳米金属多层膜力学性能的报道较少[10−11]。因此,有必要对纳米金属多层膜的拉伸性能(强度)进行系统的研究,以阐明其尺寸依赖性。
目前,关于金属多层膜强度/硬度的理论机制主要有以下3种:1) 基于类似于Hall-Petch关系的强化模型,即 σy∝(hM)−α(σy为屈服强度;hM为单层厚度;α为指数)[4,8,12]。大量研究结果表明:当hM>100 nm时,指数 α=0.5;当(hM<100 nm)时,指数 α<0.5。2) 基于被界面定扎的单个位错在软相滑移的束缚层滑移(Confined layer slip, CLS)模 型[1,8,13], 即 σy与(bμ/hM)ln(hM/b)成比例 (b和μ分别是软相材料的伯氏矢量和剪切模量)。3) 界面强度模型,此模型主要考虑了模量失配[14]和/或失配位错与界面的交互作用[15−16]。MISRA 等[8]结合 Hall-Petch 关系(hM>100 nm)和CLS模型(hM<100 nm),提出了面心立方(FCC)/体心立方(BCC)金属多层膜的全尺度强度/硬度变化机制,此变化机制与实验结果吻合较好。然而,目前关于多层膜强度/硬度的实验结果及以上强化模型只针对于调制比η=1即各单层厚度相等的情况。对于具有不同调制比的金属多层膜强度/硬度的变化规律,上述强化模型的适用性是亟待研究的问题。因此,本文作者研究具有不同特征尺寸的Cu-Cr纳米金属多层膜的拉伸性能及其尺寸效应,这对深入理解 FCC/BCC体系金属多层膜的介观服役特性具有重要的工程意义和理论价值。

图1 调制周期为50和100 nm的聚酰亚胺基体Cu-Cr纳米多层膜的应力—应变曲线及硅基体 Cu-Cr纳米多层膜的载荷—深度曲线Fig.1 Typical stress—strain curves of Cu-Cr nanostructured multilayers with modulation period (λ) of 50 and 100 nm on polyimide substrate (a) and typical load—depth curves of Cu-Cr nanostructured multilayers with modulation period λ of 50 and 100 nm on Si substrate (b)
1 实验
1.1 样品制备及微观结构表征
采用UDP450型闭合场非平衡磁控溅射离子镀设备在125 μm厚的狗骨状聚酰亚胺基体以及〈111〉单晶硅基体上分别制备具有相同调制比 η(定义为 Cr单层厚度hCr与Cu单层厚度hCu之比,即η=hCr/hCu=1)、不同调制周期 λ(λ=hCr+hCu=10~250 nm)以及相同调制周期 λ(λ=25 nm)、不同调制波比 η (η=0.11~3)的 500 nm厚Cu-Cr纳米金属多层膜。表层为Cu层,Cr层与基体表面相结合。溅射沉积前,采用1 keV Ar+离子轰击清洗基体5 min,磁控溅射的本底真空约为1×10−4Pa,镀膜偏压为75 V。沉积态的Cu-Cr纳米金属多层膜试样在真空腔中于150 ℃退火2 h,以稳定组织和消除残余应力。实验用7000S型X射线衍射仪(XRD) (Cu Kα射线, 40 mA, 40 kV, θ−2θ扫描方式) 表征多层膜微结构并测定残余应力,采用石墨单色器, 步长为 0.02°,扫描速率为0.1(°)/s,使用去除 Kα2的程序扣除诸线的Kα2衍射峰。通过JEOL−2100F透射电子显微镜(TEM)对Cu-Cr多层膜样品进行微观结构分析。
1.2 力学性能测试
室温下,采用 Micro-force test system (MTS®Tytron 250)对聚酰亚胺基体Cu-Cr多层膜进行单轴拉伸试验,试样标距部分为30 mm×3 mm(长×宽),应变速率为 1×10−4s−1。拉伸实验采用恒位移控制。薄膜/基体系的载荷及位移数据由试验机和高分辨率激光检测系统自动记录。为了得到薄膜本身的载荷,对相同几何尺寸的聚酰亚胺基体也进行拉伸测试,并记录其载荷及位移。采用应力分离法[17−18]得到多层膜的本征拉伸响应,获得屈服强度(σ0.2),如图1(a)所示。
试验中使用 MTS 公司生产的 Nano-Indenter XP型纳米压入仪(采用Berkovich 三棱锥金刚石压头,载荷分辨率为50 nN,位移分辨率为0.1 nm),采用准静态法(Oliver-Pharr方法[19],简称 O&P方法)在室温下测量Cu-Cr多层膜的硬度,最大压入深度为100 nm,如图1(b)所示。为保证测试的可靠性,对每个样品至少行测量8 次,各测试点的间距大于50 μm,取其平均值作为多层膜的硬度。
2 结果与讨论
2.1 微观结构
图2所示为不同调制周期 Cu-Cr多层膜(η=1)的XRD 谱。图2表明:FCC 结构的Cu层具有(111)择优取向,BCC结构的Cr层具有(110)择优取向。随着调制周期λ的减小,Cu-(111)和Cr-(110)的衍射峰强度降低且逐渐宽化,呈现纳米晶结构特征。采用“sin2ψ”方法计算后发现:150 ℃退火2 h后,各Cu-Cr纳米多层膜的残余应力为100~300 MPa,远低于其相应的屈服强度[20−21]。

图2 调制比 η=1时不同调制周期的 Cu-Cr纳米多层膜的XRD谱Fig.2 XRD patterns of Cu-Cr nanostructured multilayers at modulation ratio of η=1 in different modulation modulation periods (λ)
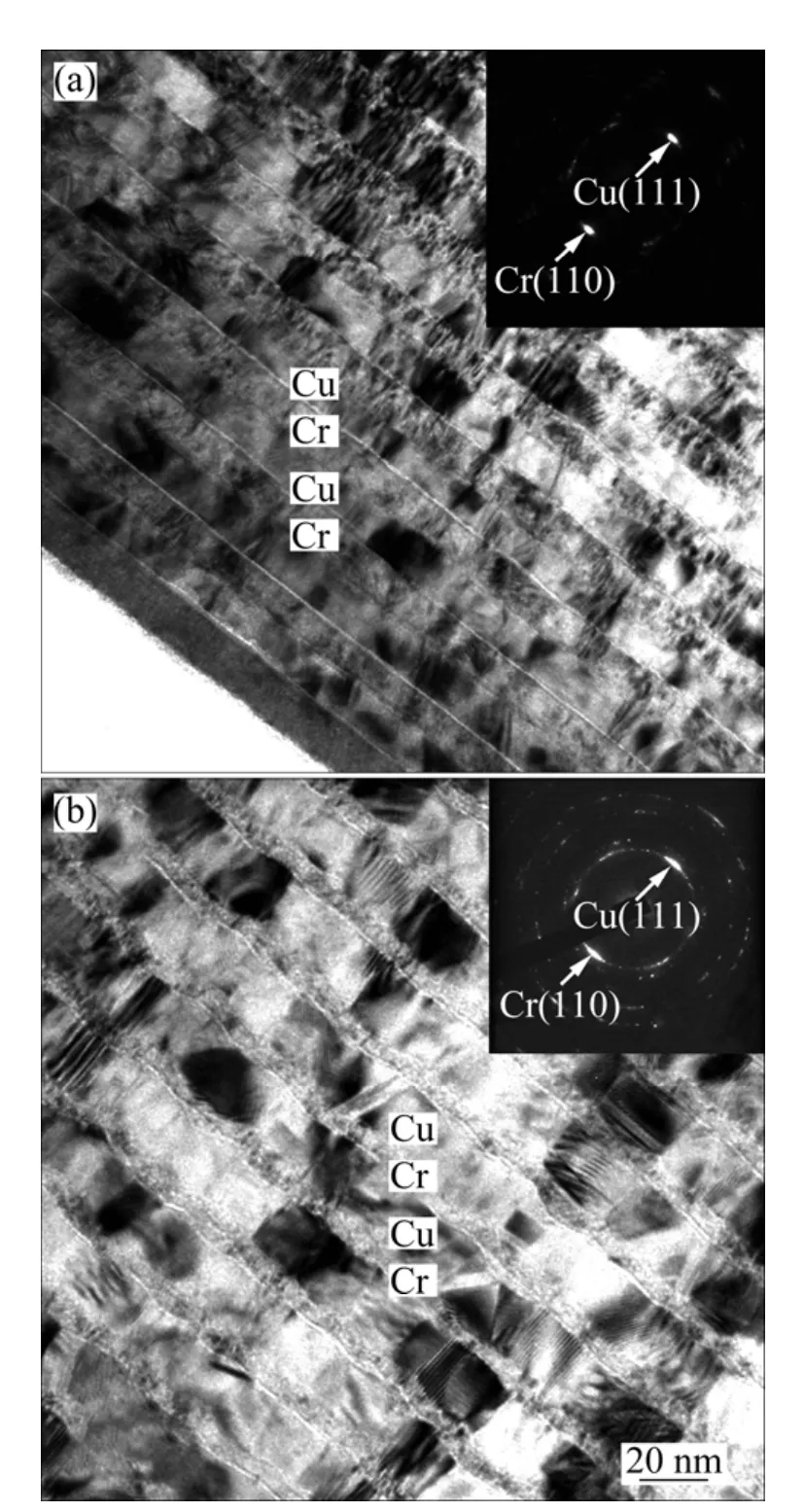
图3 所示为不同调制比及λ=25 nm的Cu-Cr纳米多层膜的TEM像和相应的选区电子衍射斑(SADP)。从图3可以看出:Cu-Cr纳米多层膜清晰地呈现组元材料周期变化的调制结构,这主要是由于Cu和Cr之间的互溶度较低,600 ℃以下则几乎不溶,且室温下溅射沉积制备没有足够的热能,导致Cu和Cr层二者互混[22]。其中:Cu层呈柱状纳米晶,Cr层呈极细小的纳米晶。晶粒尺寸随着单层厚度的减小而减小。从SADP可以看出:Cu与Cr层在生长方向呈现明显的Kurdjumov−Sachs (K−S)取 向 关 系[11],即 {111}Cu//{110}Cr和〈110〉Cu//〈111〉Cr,这与 XRD 结果一致。进一步的微观分析表明:基体对Cu-Cr纳米多层膜的微观结构无影响,这可能是由于室温下溅射沉积及基体温度较低造成的。
2.2 屈服强度/硬度及其强化模型
图4所示为柔性基体 Cu-Cr多层膜的屈服强度(σ0.2)与调制周期和调制比的关系。图4中实线是通过CLS模型计算得到的束缚层单根位错滑移所需应力(σcls);虚线是通过混合法则计算得到的多层膜的复合强度(σmix)。由图 4 可知:在调制比一定的情况下(η=1),Cu-Cr多层膜的屈服强度随调制周期(或单层厚度 hM)的减小而增大;当调制周期小于25 nm或hM小于12.5 nm时,屈服强度变化不大,如图4(a)所示。这与MISRA和 KUNG[4]的实验结果是一致的。屈服强度的这一变化趋势说明变形机制可能在某一临界尺寸发生了转变。在调制周期一定的情况下(λ=25 nm),Cu-Cr多层膜的屈服强度随调制比(或硬相Cr的体积分数)的增加而增加;当调制比η>1时,屈服强度缓慢增加,如图4(b)所示。屈服强度的增加除了特征结构对位错活动约束效应外,主要是由于硬相Cr体积分数的增加。此外,Cu-Cr多层膜的屈服强度明显高于相同厚度纯铜薄膜的屈服强度。这主要归因于特征尺寸(膜厚h和晶粒尺寸d)以及界面对位错形核、运动的抑制约束[1,4,8]。

图4 Cu-Cr纳米多层膜的屈服强度(σ0.2)与调制周期和调制比的关系Fig.4 Yield strength (σ0.2) of Cu-Cr nanostructured multilayers as function of modulation period λ (a) and modulation ratio η (b)

图5 Cu-Cr纳米多层膜的硬度(H)与调制周期(a)和调制比(b)的关系Fig.5 Hardness (H) of present Cu-Cr nanostructured multilayers as function of modulation period (λ) at η=1 (a) and modulation ratio (η) at λ=25 nm (b)
图5 所示为调制周期以及调制比对Cu-Cr多层膜硬度(H)的影响。纳米压入结果表明,Cu-Cr多层膜的硬度与其屈服强度的变化趋势相似。Cu-Cr多层膜(η=1)的硬度随调制周期的减小而增加,当调制周期小于某一临界尺寸(约为 25 nm)时,硬度达到饱和值,如图5(a)所示。并且本实验中 Cu-Cr多层膜的硬度明显高于文献[4]中的硬度。这主要是由于前者总厚度仅为500 nm,而后者的总厚度为1 μm。另外,Cu-Cr多层膜的微观结构也可能存在差异。对于调制周期恒定(λ=25 nm)的 Cu-Cr多层膜而言,当调制比小于1时,其硬度随调制比的增加急剧增加;当调制比大于某一临界值(约为1)时,硬度随调制比的增加缓慢增加,如图5(b)所示。此外,硬度值相当于屈服强度的5~6倍。这主要是由于硬度值相当于 7%~8%的塑性应变所对应的应力[4,8,11],而屈服强度仅相当于大约1%的塑性应变所对应的流变应力。
金属多层膜由异质材料交叠调制而成,其变形最先(或最易)受到某一主导相(软相)的控制[1,13]。对于Cu-Cr多层膜,Cu为软相,先发生塑性变形。在多晶薄膜中,强度由微结构尺寸(膜厚h和晶粒尺寸d)中较小者决定。但本实验中,Cu层的晶粒尺寸大于其单层厚度,因此,这里主要讨论 Cu层厚度对屈服强度的影响。根据CLS模型,Cu层单根位错滑移所需应力(σcls)可以表示为[1,8]
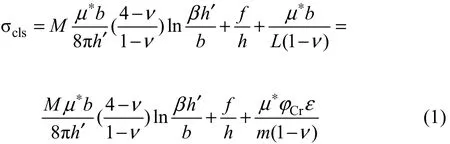
式中:M 为泰勒常数;h′为平行于滑移面的层厚;b为柏氏矢量的绝对值;v为 Cu的泊松比;β为位错芯参数;f为界面应力;Cu-Cr多层膜的平均剪切模量,μCu与 φCu分别为 Cu的剪切模量和Cu层的体积分数,Cr层亦然;L为平行排列的滑移位错环间距(L=bm/(εφCr))[1],ε为面内塑性应变,m为激活滑移系的应变因子,约为0.5)。拉伸实验结果[10−11]表明:纳米金属多层膜在最初的1%~2%的塑性应变后表现出较低的加工硬化速率。MISRA等[8]发现:在CLS模型中,1%~ 2%的塑性应变所对应的流变应力能够很好地吻合强度数值。根据这些结果以及式(1),在本实验中选 ε为 1%来计算Cu-Cr多层膜的屈服强度。其他参数值选取为M=3,μCu=48.3 GPa,μCr=115.4 GPa,ν =0.343,b=0.255 6 nm,β= 0.2,f =3 J/m2,ε=1%, h′=h,图 4(a)与(b)分别表示σcls与调制周期和调制比的关系。如图4(a)所示,当调制比恒定(η=1)且调制周期大于25 nm时,计算值与实验结果吻合较好;进一步减小调制周期,CLS模型计算得到的屈服强度明显偏高。当调制周期恒定(λ=25 nm )且调制比小于1时,CLS模型也能够很好地吻合实验值;当调制比大于1时,CLS模型不再适用。这是因为Cu层(厚度小于12.5 nm)中位错的被界面强烈钉扎,导致Cu层脆化和Cr层一样。这时,Cu-Cr多层膜可以视为两相复合材料。根据复合材料屈服强度混合法则,其屈服强度(σmix)可以表示为

3 结论
1) 具有非共格界面的 Cu-Cr纳米金属多层膜调制结构清晰,在生长方向上具有择优取向,表现出Kurdjumov–Sachs (K−S)取向关系:{111}Cu//{110}Cr且〈110〉Cu//〈111〉Cr。
2) Cu-Cr纳米金属多层膜的屈服强度/硬度具有强烈的尺寸(调制周期以及调制比)依赖性。当调制比恒定(η=1)时,多层膜的屈服强度/硬度随调制周期的减小而增大;当调制周期小于某一临界尺寸(约为 25 nm)时,屈服强度/硬度达到饱和值。当调制周期恒定(λ=25 nm)时,多层膜的屈服强度/硬度随调制比的增大而增大;当调制比大于某一临界值(约为1) 时,屈服强度/硬度变化缓慢。当调制比η=1的Cu-Cr多层膜的调制周期大于此临界调制周期或调制周期 λ=25 nm 的Cu-Cr多层膜的调制比小于临界调制比时,Cu-Cr多层膜的屈服强度可以通过CLS模型拟合;反之,可以采用复合材料强度混合法则进行计算。
REFERENCES
[1] EMBURY J D, HIRTH J P. On dislocation storage and the mechanical response of fine scale microstructures[J]. Acta Metall Mater, 1994, 42(6): 2051−2056.
[2] DAYAL P, SAWIDES N, HOFFMAN M. Characterisation of nanolayered aluminium/palladium thin films using nanoindentation[J]. Thin Solid Films, 2009, 517(13): 3698−3703.
[3] ANDERSON P M, CARPENTER J S. Estimates of interfacial properties in Cu/Ni multilayer thin films using hardness data[J].Scripta Mater, 2010, 62(6): 325−328.
[4] MISRA A, KUNG H. Deformation behavior of nanostructured metallic multilayers[J]. Advanced Eng Mater, 2001, 3(4):217−222.
[5] WEN S P, ZONG R L, ZENG F, GAO Y, PAN F. Evaluating modulus and hardness enhancement in evaporated Cu/W multilayers[J]. Acta Mater, 2007, 55(1): 345−351.
[6] LAI W S, YANG M J. Observation of largely enhanced hardness in nanomultilayers of the Ag-Nb system with positive enthalpy of formation[J]. Appl Phys Lett, 2007, 90(18): 181917−1−3.
[7] HAN S M, PHILLIPS M A, NIX W D. Study of strain softening behavior of Al-Al3Sc multilayers using microcompression testing[J]. Acta Mater, 2009, 57(15): 4473−4490.
[8] MISRA A, HIRTH J P, HOAGLAND R G.Length-scale-dependent deformation mechanisms in incoherent metallic multilayered composites[J]. Acta Mater, 2005, 53(18):4817−4824.
[9] MARA N A, BHATTACHARYYA D, DICKERSON P,HOAGLAND R G, MISRA A. Deformability of ultrahigh strength 5 nm Cu/Nb nanolayered composites[J]. Appl Phys Lett,2008, 92(23): 231901−1−3.
[10] WANG Y M, LI J, HAMZA A V, BARBEE J T W. Ductile crystalline-amorphous nanolaminates[J]. Proc Natl Acad Sci USA, 2007, 104(27): 11155−11160.
[11] MARA N A, BHATTACHARYYA D, HOAGLAND R G,MISRA A. Tensile behavior of 40 nm Cu/Nb nanoscale multilayers[J]. Scripta Mater, 2008, 58(10): 874−877.
[12] ANDERSON P M, LI C. Hall-Petch relations for multilayered materials[J]. Nanostruct Mater, 1995, 5(3): 349−362.
[13] PHILLIPS M A, CLEMENS B M, NIX W D. A model for dislocation behavior during deformation of Al/Al3Sc (fcc/L12)metallic multilayers[J]. Acta Mater, 2003, 51(11): 3157−3170.
[14] KOEHLER J S. Attempt to design a strong solid[J]. Phys Rev B,1970, 2(2): 547−551.
[15] RAO S I, HAZZLEDINE P M. Atomistic simulations of dislocation-interface interactions in the Cu-Ni multilayer system[J]. Philos Mag A, 2000, 80(9): 2011−2040.
[16] HOAGLAND R G, KURTZ R J, HENAGER C H. Slip resistance of interfaces and the strength of metallic multilayer composites[J]. Scripta Mater, 2004, 50(6): 775−779.
[17] YU W D Y, SPAEPEN F. The yield strength of thin copper films on Kapton[J]. J Appl Phys, 2004, 95(6): 2991−2997.
[18] NIU R M, LIU G, WANG C, ZHANG G, DING X D, SUN J.Thickness dependent critical strain in submicron Cu films adherent to polymer substrate[J]. Appl Phys Lett, 2007, 90(16):161907−1−3.
[19] OLIVER W C, PHARR G M. An improved technique for determining hardness and elastic modulus using load and displacements sending indentation experiments[J]. J Mater Res,1992, 7(6): 1564−1583.
[20] ZHANG J Y, LIU G, ZHANG X, ZHANG G J, SUN J, MA E. Amaximum in ductility and fracture toughness in nanostructured Cu/Cr multilayer films[J]. Scripta Mater, 2010, 62(6): 333−336.
[21] ZHANG J Y, ZHANG X, LIU G, ZHANG G J, SUN J. Scaling of the ductility with yield strength in nanostructured Cu/Cr multilayer films[J]. Scripta Mater, 2010, 63(1): 101−104.
[22] FU E G, LI N, MISRA A, HOAGLAND R G, WANG H,ZHANG X. Mechanical properties of sputtered Cu/V and Al/Nb multilayer films[J]. Mater Sci Eng A, 2008, 493(1/2): 283−287.
Size-dependent yield strength and hardness of Cu-Cr nanostructured metallic multilayers
ZHANG Jin-yu, NIU Jia-jia, ZHANG Xin, LEI Shi-ying, ZHANG Peng, LIU Gang, SUN Jun
(State Key Laboratory for Mechanical Behavior of Materials, Xi’an Jiaotong University, Xi’an 710049, China)
Polyimide-supported and silicon-supported Cu-Cr nanostructured metallic multilayers with constant modulation ratio (η) and constant modulation period (λ) were respectively synthesized by means of direct current (DC)magnetron sputtering. The size-dependent yield strength and hardness of Cu-Cr multilayers were respectively investigated by uniaxial tensile test and nanoindentation test. It is revealed from the microstructure analysis that the substrates have no influence on the microstructure of Cu-Cr multilayers, and that the layers are textured in the growth direction with the Kurdjumov-Sachs orientation relationship, i.e., {111}Cu//{110}Cr and 〈110〉Cu//〈111〉Cr. The mechanical test results show that both the yield strength and hardness of Cu-Cr multilayers with constant η increase with reducing λ, while those of the ones with constant λ increase with increasing η. The deformation mechanism of Cu-Cr nanostructured metallic multilayers transit from the slide of single dislocation confined to individual Cu layers to the load bearing effect at a critical modulation period λc(≈25 nm) or a critical modulation ratio ηc( ≈1).
nanostructured metallic multilayers; strength; hardness; modulation period; modulation ratio
TG113
A
1004-0609(2011)03-0618-06
国家重点基础研究发展计划资助项目(2010CB631003);国家自然科学基金资助项目(50971097)
2010-08-26;
2010-09-29
张金钰,博士;电话: 13484549249;E-mail: jinyuzhang@stu.xjtu.edu.cn
(编辑 陈卫萍)
