带有 p-Lap lacian算子的二阶微分方程组多个正解的存在性

王 斌,江卫华,黄晓芹,李国刚

(1.河北化工医药职业技术学院基础部,河北石家庄 050026;2.河北科技大学理学院,河北石家庄 050018)

带有 p-Lap lacian算子的二阶微分方程组多个正解的存在性

王 斌1,江卫华2,黄晓芹2,李国刚2

(1.河北化工医药职业技术学院基础部,河北石家庄 050026;2.河北科技大学理学院,河北石家庄 050018)

利用五个泛函的不动点定理,研究带有 p-Lap lacian算子的二阶微分方程组分别在3种边界条件下至少3个正解的存在性,并给出例子验证所得结论。

p-Lap lacian算子;五个泛函的不动点定理;锥;正解

对于带有 p-Lap lacian算子的微分方程的研究已有很多结论[1-4],文献[1-2]分别利用锥上的不动点定理和五个泛函的不动点定理研究了带有 p-Lap lacian算子的二阶微分方程正解的存在性。文献[3-4]分别利用锥上的不动点指数理论和锥拉伸和锥压缩不动点定理给出了带有 p-Lap lacian算子的微分方程组边值问题至少1个正解存在的条件,笔者利用五个泛函的不动点定理研究带有 p-Lap lacian算子的二阶微分方程组

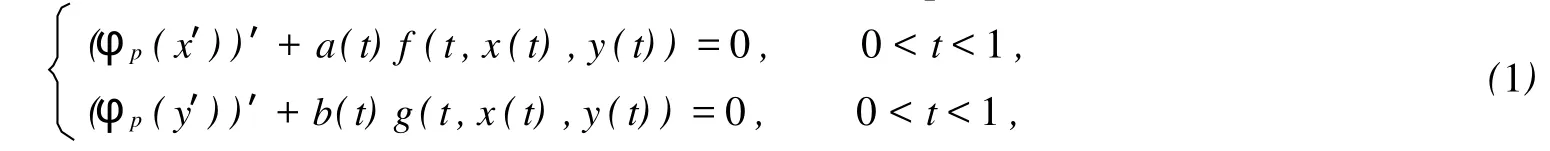
分别在

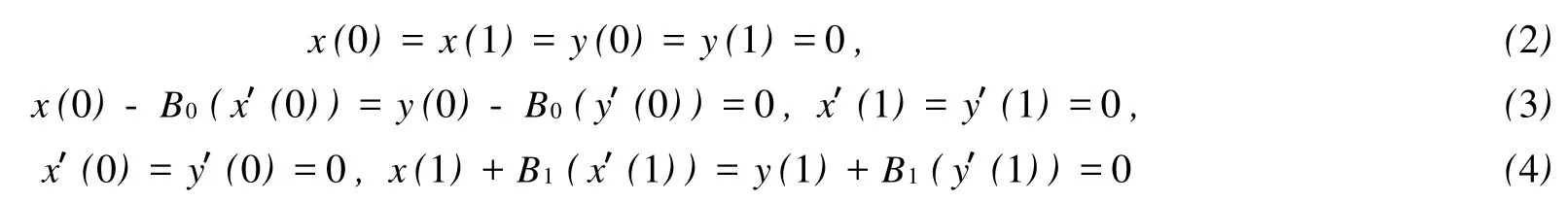
的边值条件下至少有3个正解的存在性,其中φp(v)=|v|p-2v。

1 主要结果

以下用到的基本概念和定理见文献[5]。假设如下条件成立:

H1)f,g:[0,1]×[0,∞)×[0,∞)→[0,∞)是连续的;

H2)B0(v)和B1(v)是2个定义在 R的连续奇函数,并且存在 m>0,使得对所有 v≥0,有0≤Bj(v)≤m v,j=0,1;其中ψp是φp的反函数。易知A为全连续算子,且(x,y)为问题(1)和(2)的解的充分必要条件是(x,y)是A的不动点。

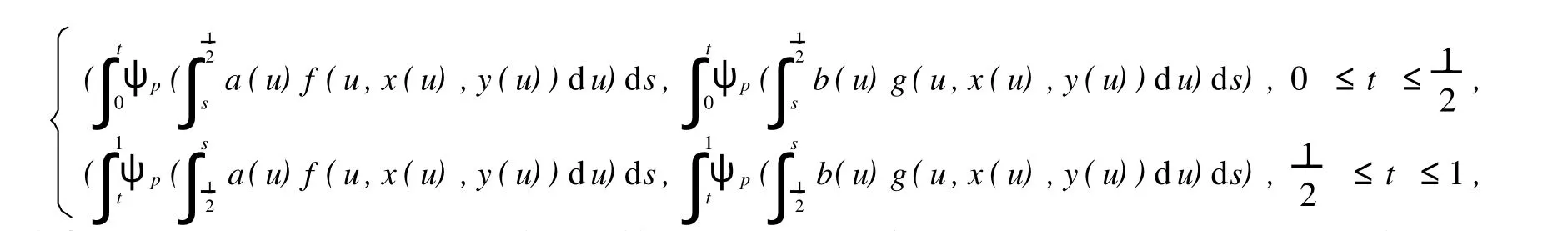
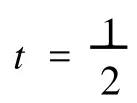
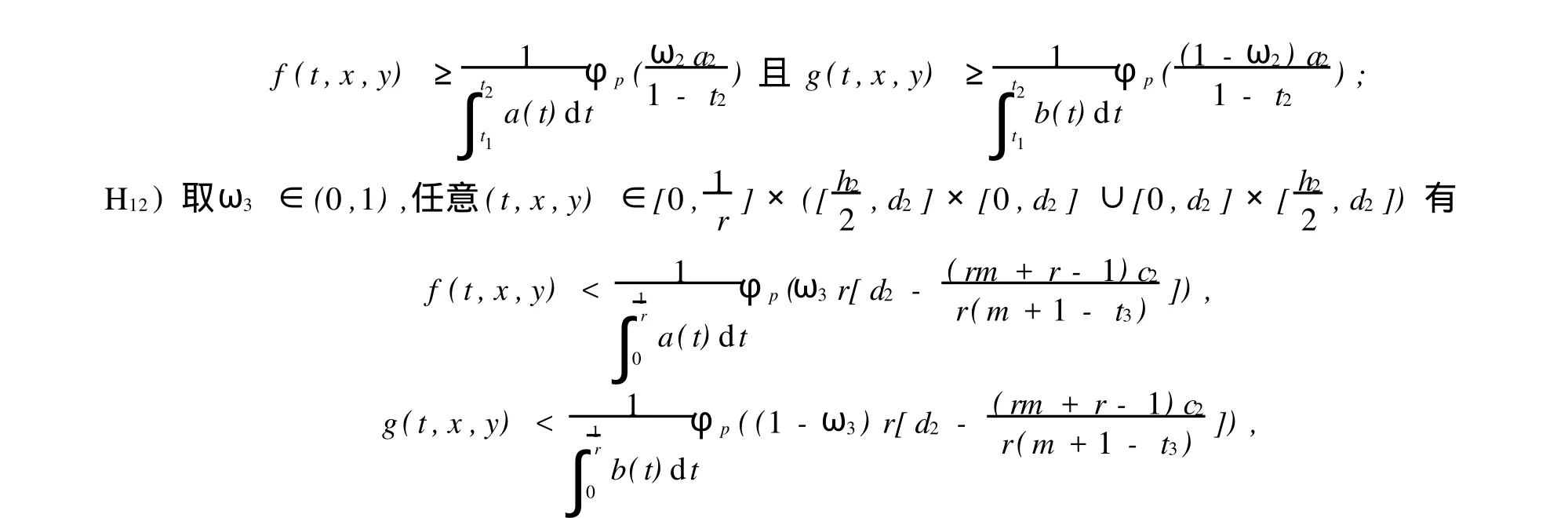
则问题(1)和(4)至少存在3对正解(xi,yi),满足

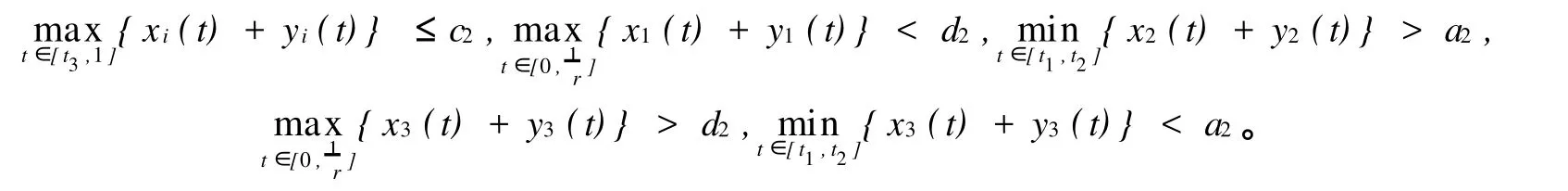
证明 定义全连续算子 T2为

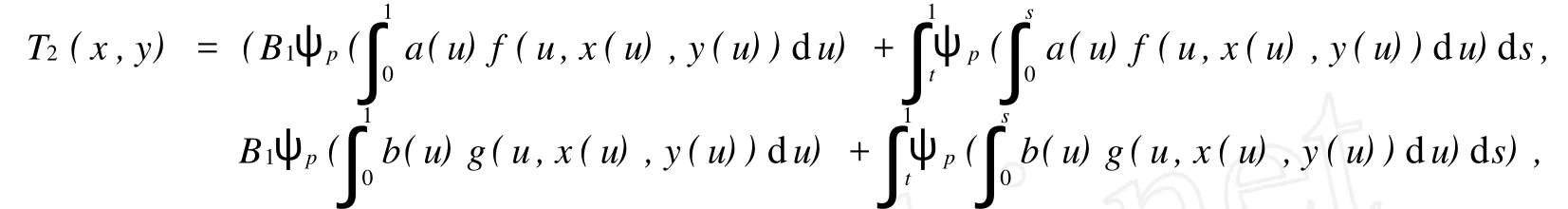
类似定理1证明可得结论成立。

2 示 例

考虑下列边值问题:

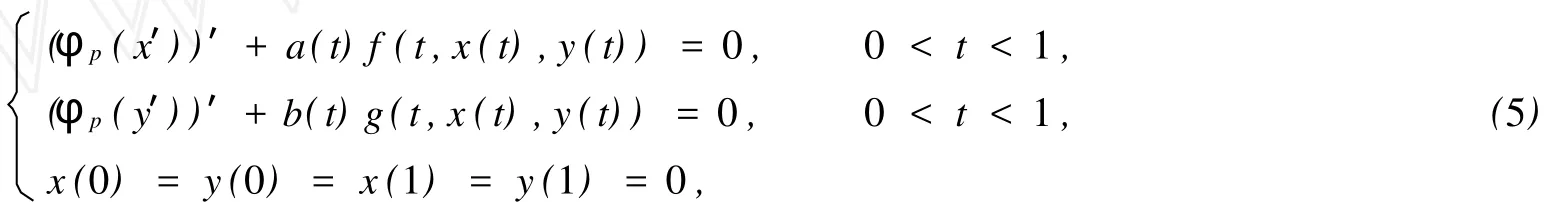
其中

[1] WANG Jun-yu.The existence of positive solutions for the one-dimensional p-Lap lacian[J].Proceedings of the American Mathematical Society,1997,125(8):2 275-2 283.

[2] GUO Yan-ping,GEWei-gao.Three positive solutions for the one-dimentional p-Laplacian[J].J Math Anal Appl,2003,286:491-508.

[3] 王 芳,钟承奎,王彩勋.一类一维奇异 p-Laplacian方程组边值问题正解的存在性[J].兰州大学学报(自然科学版)(Journal of Lanzhou University(Natural Sciences)),2009,45(1):103-106.

[4] 田元生,刘春根.p-拉普拉斯四点边值问题拟对称正解的多重性[J].系统科学与数学(Journal of System Science and Mathematical Science),2010,30(3):349-357.

[5] ZHANGB,L IU X.Existence of multiple symmetric positive solutions of higher order Lidstone p roblems[J].J Math Anal Appl,2003,284:672-689.

Existence of multiple positive solutions of second-order differential system s w ith p-Laplacian

WANGBin1,JIANGWei-hua2,HUANG Xiao-qin2,L IGuo-gang2

(1.Department of Basic Courses,Hebei Professional and Technological College of Chemical and Pharmaceutical Engineering,Shijiazhuang Hebei 050026,China;2.College of Sciences,Hebei University of Science and Technology,Shijiazhuang Hebei 050018,China)

Using five functions fixed point theorem,we p rove the existence of at least three positive solutions to second-order system s w ith p-Lap lacian under three kindsof boundary conditions,respectively.We give an examp le to illustrate our result.

p-Laplacian operator;five functions fixed point theo rem;cone;positive solution

O152.7

A

1008-1542(2011)01-0015-05

2010-06-15;

2010-10-10;责任编辑:张 军

国家自然科学基金资助项目(10875094);河北省自然科学基金资助项目(A2009000664)

王 斌(1964-),男,河北石家庄人,副教授,主要从事微分方程方面的研究。