多散射杂质对二维电子系统输运特性的影响
2011-11-02白志明
白志明,马 强
(河北科技大学理学院,河北石家庄 050018)
多散射杂质对二维电子系统输运特性的影响
白志明,马 强
(河北科技大学理学院,河北石家庄 050018)
利用散射矩阵理论研究了含有多个矩形散射杂质二维系统中电子输运问题。绝对零度下,电导随入射电子能量增大,呈台阶式上升形式;杂质宽度的减小使得电导的量子化现象增强;杂质长度的增大,使得电导在最初阶段急剧减小,而后呈现周期性振荡;随着散射杂质数量的增加,电导由急剧减小也呈现周期性振荡。温度的升高使得电导台阶倾斜,量子化现象逐渐消失。
杂质;电导量子化;散射矩阵理论
在凝聚态物理中,研究电子输运现象已有很长时间,研究对象绝大多数是室温下的宏观物体。室温下,由晶格振动所引起的非弹性效应会非常频繁地作用于电子,使其带有的相位信息被破坏掉[1-9],因此,电子的波动性已几乎不起作用,于是电子的粒子性占据了主导地位,所运用的理论通常也是经典与半经典的方法(比如,经典的玻尔兹曼方程,它把电子看成是具有确定位置和动量的经典粒子,受到外场、晶格振动、杂质和缺陷的共同作用)。尽管像玻尔兹曼方程这样的方法在上述领域中已经取得了不错的成果,但是还有很大的局限性,它很难解决电子波动性起主要作用的电子输运问题。因为当所研究的体系尺度小到可以和电子的德布罗意波长相比较,且在低温的情况下时,电子的波动性将起到明显的作用。而根据不确定关系,这时体系中的电子不能同时具有确定的位置和确定的动量。在这样的情况下,很多经典的概念和方法是失效的。为了研究这种微小体系的物理特性,需要用量子理论进行研究。上述的微小体系正好属于介观体系的范畴。电子器件一旦做到介观尺度,在研究电子输运时就不得不考虑电子的相干性。为此,人们做了大量的实验和理论性工作,提出了一些理论模型和数值计算方法。散射矩阵理论方法[10-12]是常用的方法之一。
在低温下,介观体系表现出很多新的量子效应现象 (其中最重要的现象就是电导量子化),为进一步对新的量子效应现象进行研究,笔者利用散射矩阵理论对含有多个矩形散射杂质的二维系统中电子波输运问题进行分析,并利用量子理论给出系统的电导。
1 理论和模型
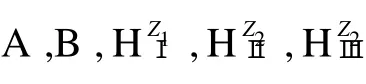


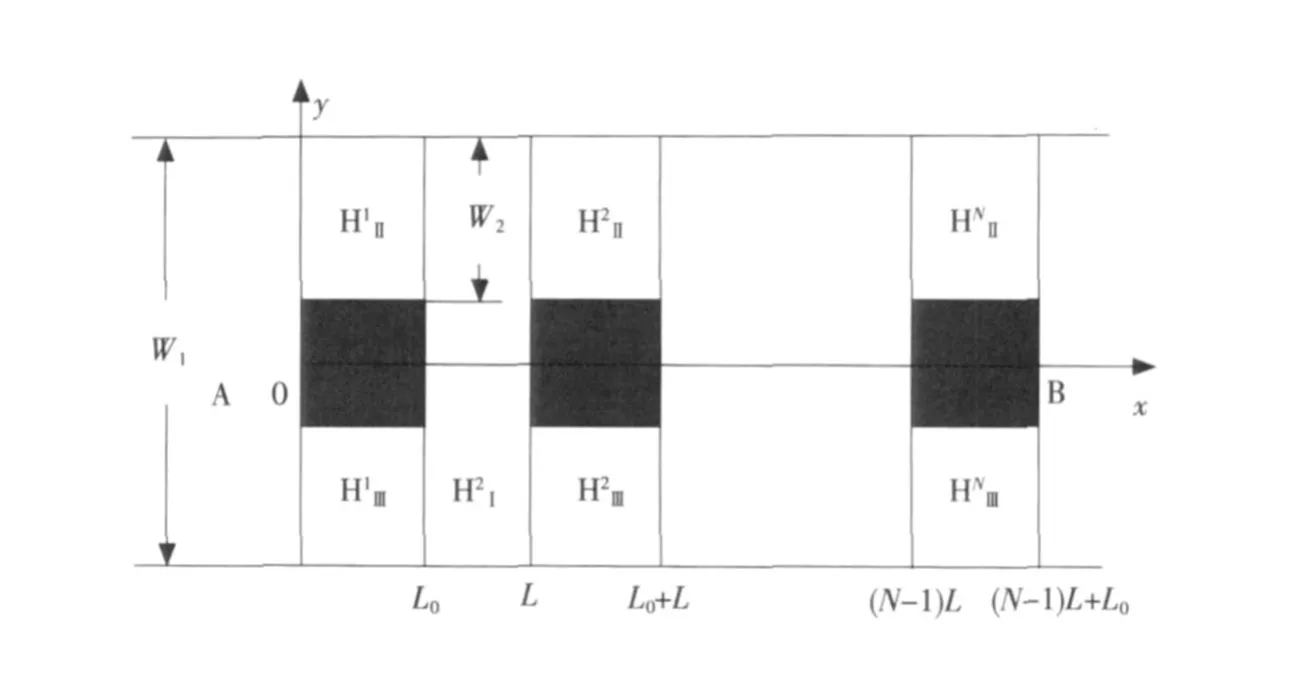
图1 含有多个散射杂质的二维电子系统Fig.1 Two-dimensional electron system w hich containsmultip le scattering impurities
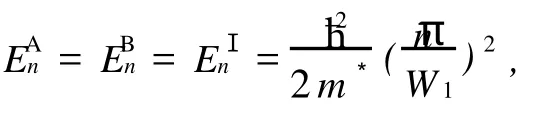
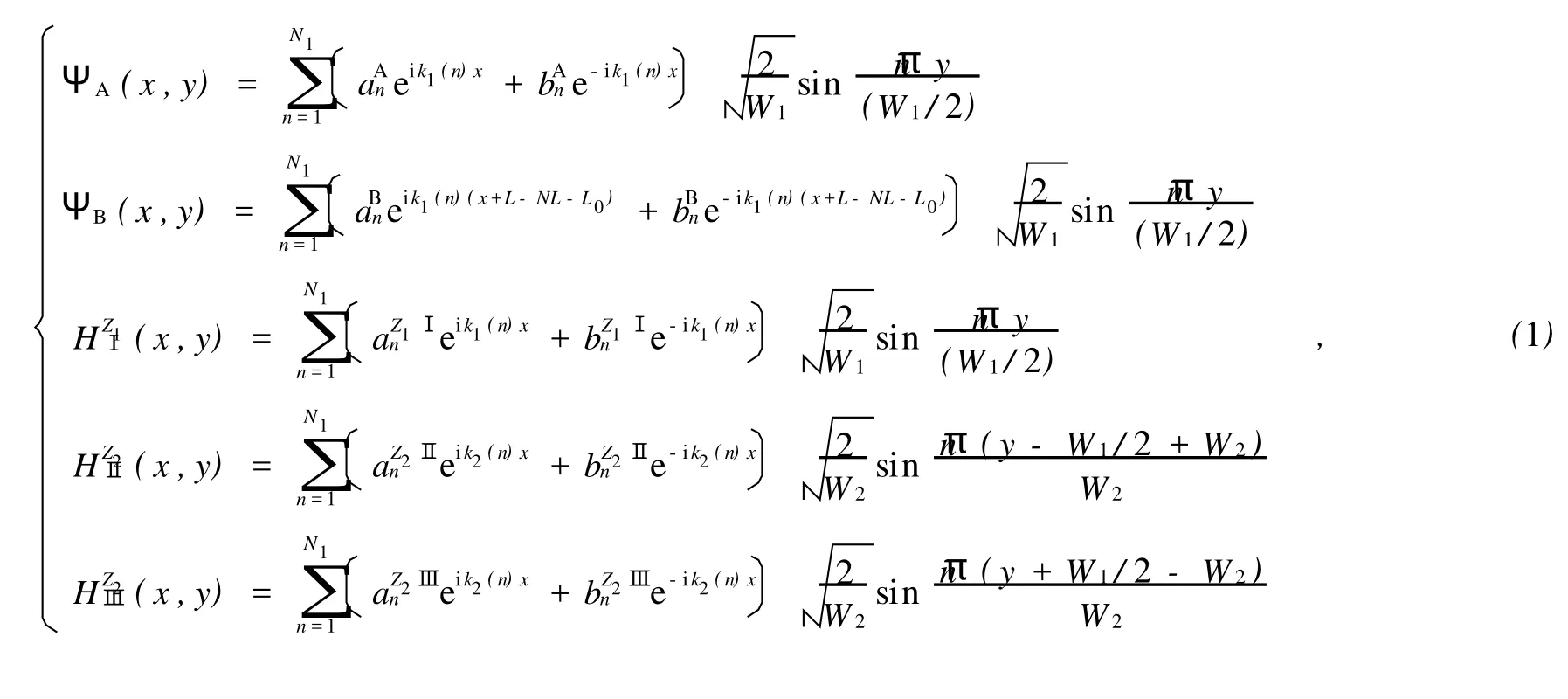
其中 Z1∈[2,N],Z2∈[1,N]。k1(n),k2(n)分别为电子在导电区域方向上不同区域 x的波矢。式(1)右端的两项分别代表向前和向后运动的电子波。N1为电子可能占据横向子能级数。电子的总能量与波矢及模向量子化能量之间有如下关系
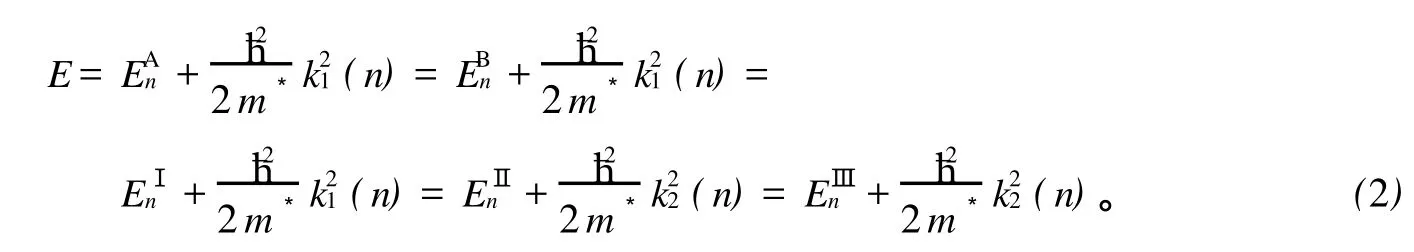
在给定的费米能量 EF下,电子输运通道数由式(2)决定。在不同区域的交界面处,电子波函数及其导数连续,因此在 x=0处有方程

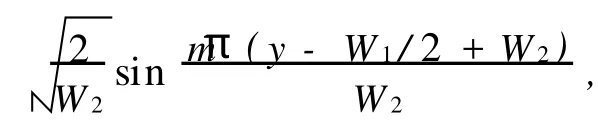

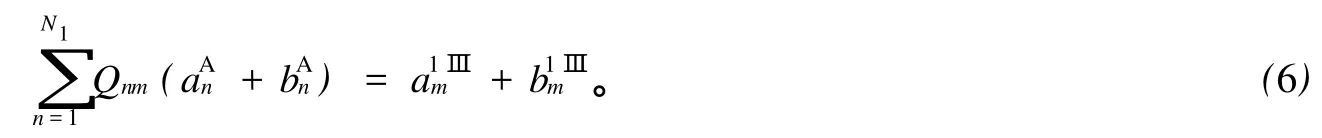
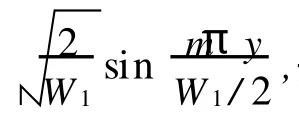
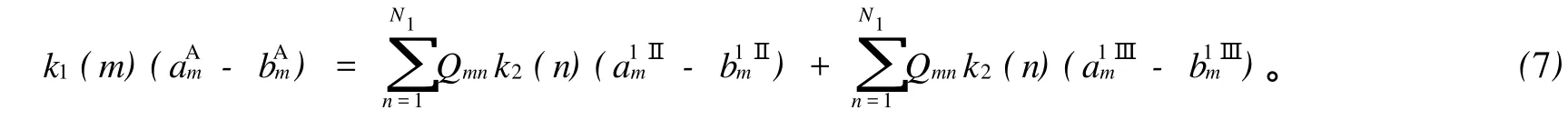
式(5)、式(6)和式(7)可以写成矩阵形式
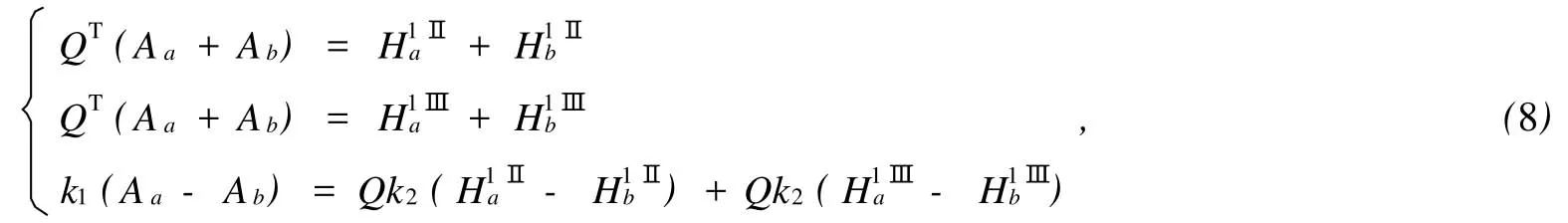
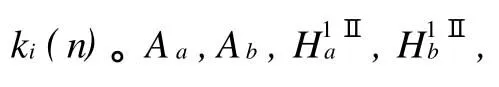
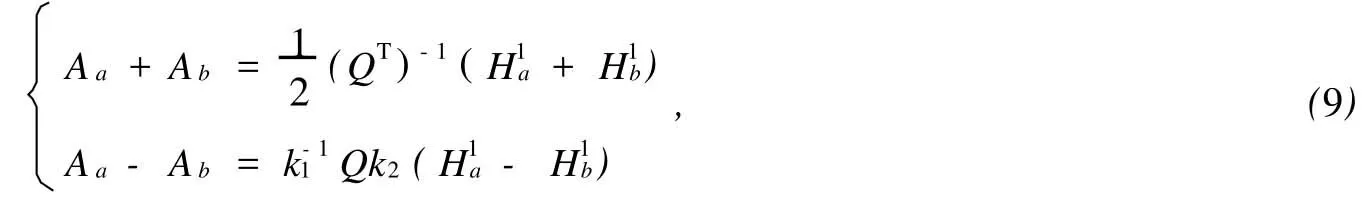
由此得到

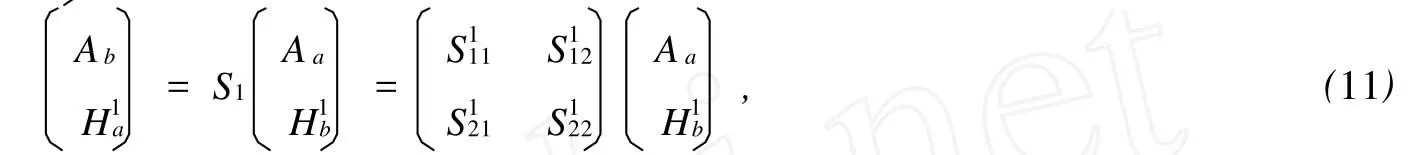
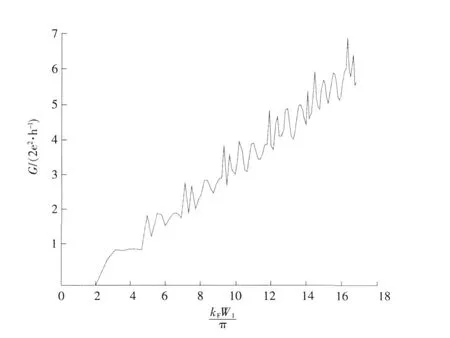
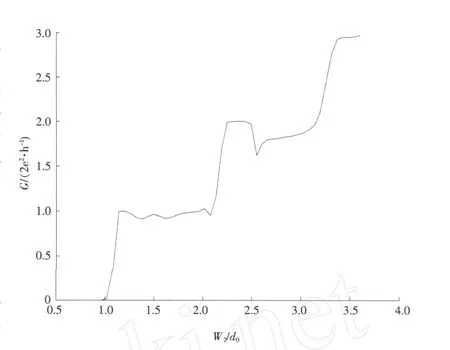
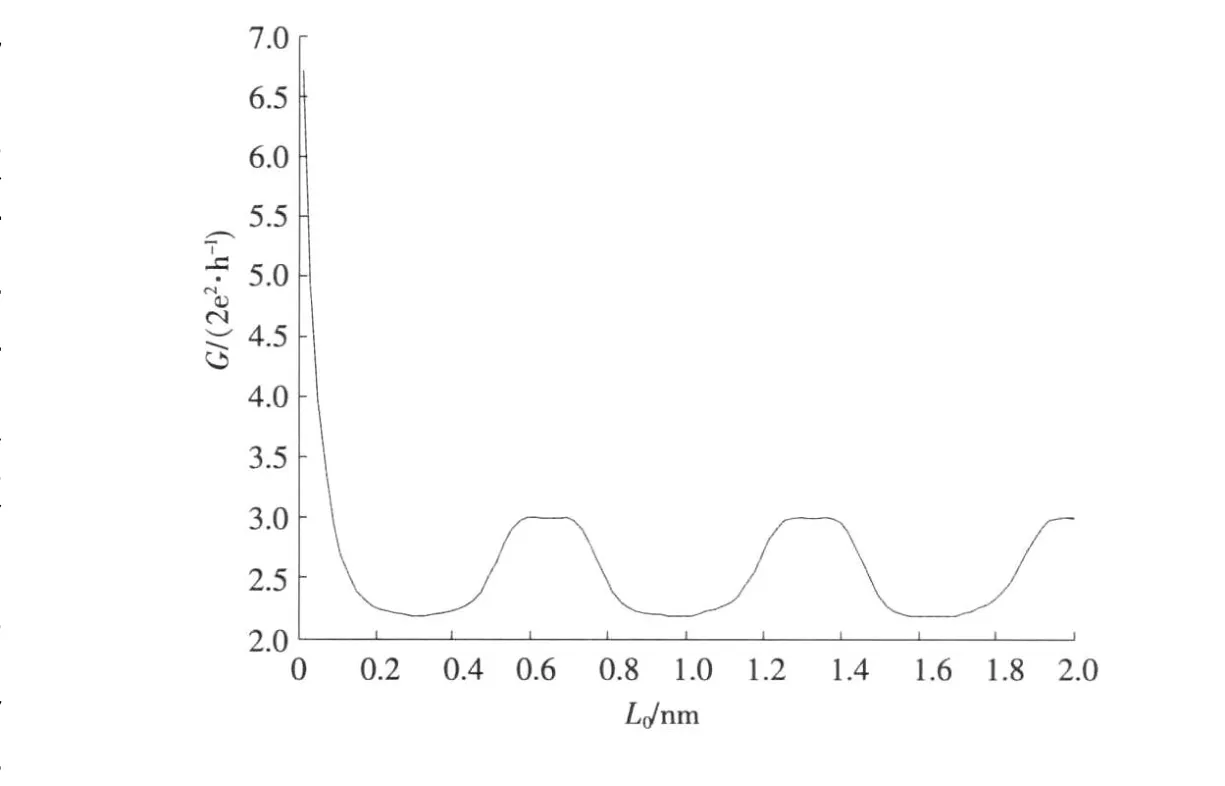
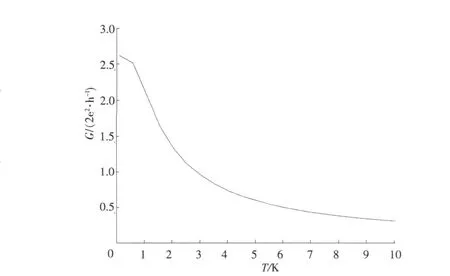
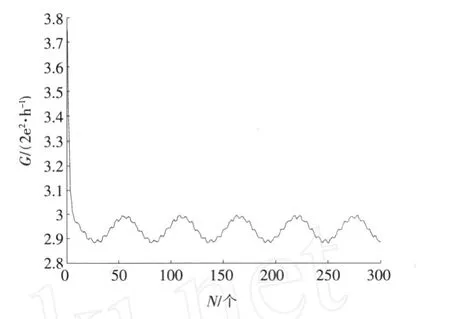
在0 同理,在 x=L0处有 在L0≤x≤L的区域内,电子波传播的散射矩阵S4可以直接写出 S4就是电子波在相邻2个矩形之间传播的散射矩阵。因此,电子波从 x=0处(即第1个矩形的左侧)传播到x=L0处(即第1个矩形的右侧)的散射矩阵为 同理得到电子波从每一个矩形散射杂质左侧传播到右侧的散射矩阵均为SA。令SB=S4⊗SA,SB为电子波从一个矩形散射杂质右侧传播到下一个矩形散射杂质右侧的散射矩阵。因此,电子波从区域A传播到区域B的总散射矩阵为 根据散射矩阵的定义,有 因此S是1个2N1×2N1维的矩阵,它将入射区域A和透射区域B中电子波的振幅联系起来。由于区域B是输出端,则由式(17)得到 若已经求得S11,S21,又因为Aa是已知的,则Ab和Ba可以容易地求得。例如:假如在区域A中只有第1个模注入,则矩阵 Aa,Ab和Ba分别为 其中rn1代表由第1个模输入,由第n个模反射的波振幅,tn1代表由第1个模输入,由第n个模透射的波振幅。k1(n)(n=1,2,…,N1)因子的引入是为了保证流守恒条件 T+R=1。因为Aa是已知的,则由式(18)得到透射率和反射率分别为 如果区域中有多个横向模的电子输入,则需要多次计算而求得总的透射率和反射率。零温下电导与透射率的关系为 而在非零温度情况下,系统电导为 图2 绝对零温下两杂质系统的电导 G随入射电子费米波矢kF的变化关系Fig.2 G VS Fermiwave vecto r of the incident electron at zero temperature for a two-impurity system 电子在散射区域 HⅡ和 HⅢ的传播过程中,当电子占据比较高的横向子能级时,由于散射杂质的存在,式(12)中的k2可能为纯虚数,此时为衰减波。由于以k2输运的电子运动路径有限,因此衰减波在数值处理过程中应予考虑。 图3 零温下两杂质系统的电导 G随着W2的变化关系Fig.3 G VS W2at absolute zero temperature fo r a two-impurity system 图4 绝对零温下两杂质系统的电导G随着L0的变化关系Fig.4 G VS L0at absdute zero temperature for a two-impurity system 图4给出了绝对零温下含有两散射杂质系统的电导 G随着L0的变化关系。参数选择为 E=5 eV,W1=2 nm,W2=0.9 nm,L=L0+0.5 nm,0.01 nm≤L0≤2 nm。在系统的尺寸和散射杂质的宽度以及间隔,还有入射电子的能量确定的情况下,随着散射杂质长度L0从0不断增大,最初阶段电导G急剧减小,接着呈现周期性振荡。当L0=0时,相对于整个导电区域中没有散射杂质,电子在传输过程中不会受到散射作用。在这样的情况下,若在区域A电子占据 N个通道,则有电导 G=NG0,此时的电导为最大值,图4中的曲线是符合这一理论解释的。当L0>0时,开始存在散射作用。在L0比较小的时候,电导G随着L0的不断增大急剧减小,电导的这种减小是一种散射效应。当L0增大到0.2 nm时,随着 L0的增大,电导 G呈现周期性振荡,周期在0.6~0.7 nm之间,振幅小于1个单位的量子电导 G0。这是一种干涉效应,是电子波动性的体现。电子在区域A中沿 x轴正向传输,遇到矩形散射杂质,受其散射作用,分为2个电导区域,电子在区域 HⅡ,HⅢ中传输,越过矩形散射杂质后,汇合到区域 HⅠ中。电子在传输的时候,经历了 N个这样的过程,最后在区域B汇合,由于系统的对称性,电导G呈现周期性振荡。 图5 含有五个杂质系统的电导 G随着 T温度的变化关系Fig.5 G VS temperiture T for a five-impurity system 图5给出了含有5个散射杂质系统的电导G随着温度 T的变化关系。参数选择为EF=5 eV,W1=2 nm,W2=0.9 nm,L=1 nm,L0=0.5 nm,0.1 K≤T≤10 K。在系统尺寸以及入射电子的能量确定的情况下,系统的电导 G随着温度 T的升高而不断减小。在绝对零温情况下,电子在导电区域传输过程中,由于受到 y方向的限制作用,其能量是量子化的,形成了电子占据通道的传输模式,从而使得电导呈现台阶式的量子化现象。温度对电导的影响是极其复杂的,本方法只是考虑了温度对费米分布函数的影响。随着温度的不断上升,只有能量集中于费米能级 EF附近几个kBT范围内的电子才对系统的电导有贡献。所以系统的电导随着温度的不断上升而逐渐减小。 图6 绝对零温下电导 G随着散射杂质个数 N的变化关系Fig.6 G VS the number of scattering impurities N at absolute zero temperature 图6给出了绝对零温下电导 G随着散射杂质个数N的变化关系。参数选择为 E=10 eV,W1=2 nm,W2=0.9 nm,L=1.5 nm,L0=1 nm。由图6看出,在系统尺寸以及间隔,还有入射电子的能量确定的情况下,随着散射杂质的个数 N的不断增大,最初阶段电导 G开始从最大值急剧地减小,接着呈现周期性振荡。这一点与图4十分相似。只有1个散射杂质时,电子波的传输受到杂质的散射分为2个导电区域,从而发生干涉作用,形成电导 G的周期性振荡;现在散射杂质变为多个,那么电子波在传输过程中每遇到1个散射杂质,就会发生1次干涉作用,所以最终总的干涉作用叠加在一起,也形成了电导G的周期性振荡的现象。 在绝对零温的情况下,当散射杂质的尺寸以及间隔确定时,随着入射电子能量的增大,电导呈现台阶式上升的量子化现象;当系统尺寸、散射杂质的长度及间隔和入射电子能量确定时,随着散射区域宽度的增大,电导呈现台阶式上升的量子化现象;当系统的尺寸和散射杂质的宽度以及间隔,还有入射电子的能量确定时,随着杂质长度从零不断增大,电导在最初阶段急剧减小,接着呈现周期性振荡;当系统和散射杂质的尺寸以及间隔,以及入射电子的能量确定时,系统的电导随着温度的升高而不断减小;当散射杂质的尺寸以及入射电子能量确定时,随着散射杂质的个数的不断增大,最初阶段电导急剧减小,接着呈现周期性振荡。 [1] HANG Xie,PING Shen.Fluctuation-induced tunneling conduction through nano-constrictions[J].Phys Rev B,2009,79:165 419. [2] X IA Jian-bai,SHENGWei-dong.On the soft wall guiding potentials in realistic quantum waveguides[J].J App l Phys,1996,79(10):7 780-7 784. [3] XIA Jian-bai.Quantum waveguide theo ry for microscopic structures[J].Phys Rev B,1992,45(7):3 593-3 599. [4] 夏建白.半导体中的输运过程[J].物理(Physics),1999,28(9):525-529. [5] 戴振宏,余亚宾,孙金祚.原子尺寸点接触中的电子输运性质[J].固体电子学研究与进展(Research and Progress of SSE Solid Slate Electronics),1997,17(4):340-346. [6] 顾本源,顾 雷.“介观”系统中的量子相干输运和性质[J].物理(Physics),1990,19(10):586-590. [7] 顾本源,史继荣.低维介观系统中磁边缘态输运特性[J].物理学进展(Progress in Physics),1998,18(2):117-138. [8] 杨玉峰,白志明.介观金属环中量子干涉晶体管对电子相干性的影响[J].河北科技大学学报(Journal of Hebei University of Science and Technology),2006,27(3):204-208. [9] 高 鹤.微波场作用下Fano效应对量子点电子态密度近藤峰的影响[J].河北科技大学学报(Journal of Hebei University of Science and Technology),2009,30(4):298-301. [10] 张 丽,余亚斌,蔡梦秋,等.相干输运中的接点问题[J].物理学报(Acta Physica Sinica),2008,57(5):3 166-3 170. [11] 王会娴,熊诗杰.四端介观量子网络中电子的相干输运性质[J].新乡学院学报(自然科学版)(Journal of Xinxiang University(Natural Science Edition)),2008,25(3):48-51. [12] 侯阳来,侯三林,卢建夺.电子在波导管中的输运研究[J].四川大学学报(自然科学版)(Journal of Sichuan University(Natural Science Edition)),2008,45(5):1 155-1 160. [13] 冯 端,金国钧.凝聚态物理(上卷)[M].北京:高等教育出版社,2003. [14] 阎守胜.现代固体物理学导论[M].北京:北京大学出版社,2008. [15] 夏建白.现代半导体物理[M].北京:北京大学出版社,2000. Influence of multi-scattering impurities on transport p roperties of two-dimensional electron system s BA IZhi-m ing,MA Qiang By using scattering matrix theory,the electron transpo rt in a two-dimensional system containing multi-rectangular scattering impurities is studied.A t zero temperature,the conductance show s the quantum phenomena w hich increasesw ith the increase of electron energy and w ith the decrease of the w idth of scattering impurities.The impurity makes the conductance decrease rapidly at its small length,and at large length the conductance show s periodic oscillation.In themulti-scattering system,the conductance no longer decreases rapidly butoscillatesw ith increasing number of scattering impurities.The increase of temperaturemakes the conductance stages tilt and the quantum phenomena disappear gradually. impurity;conductance quantization;scattering matrix theory O469;O481.3 A 1008-1542(2011)01-0001-07 2010-05-07; 2010-09-21;责任编辑:王士忠 白志明(1962-),男,河北冀州人,教授,博士,主要从事凝聚态物理理论方面的研究。
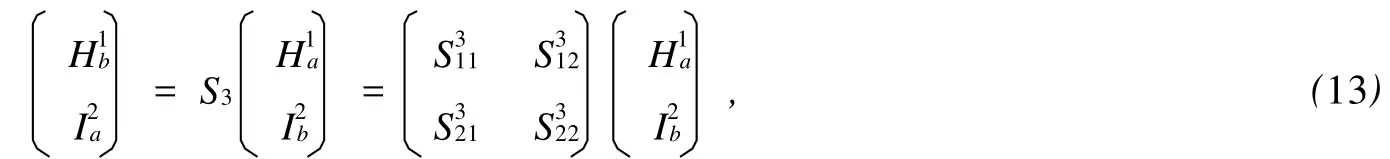
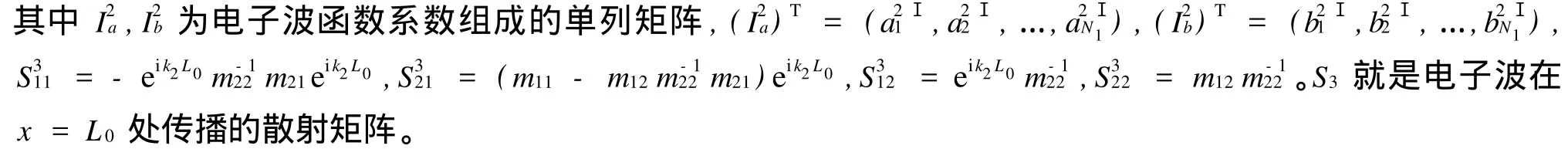


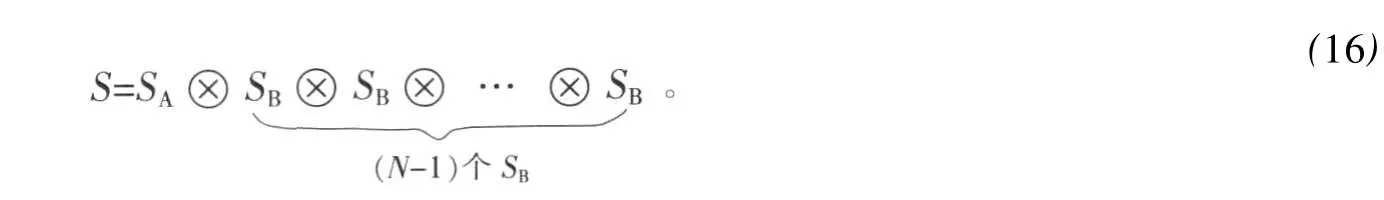
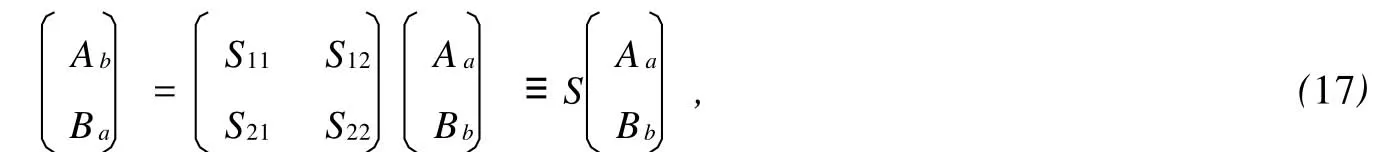

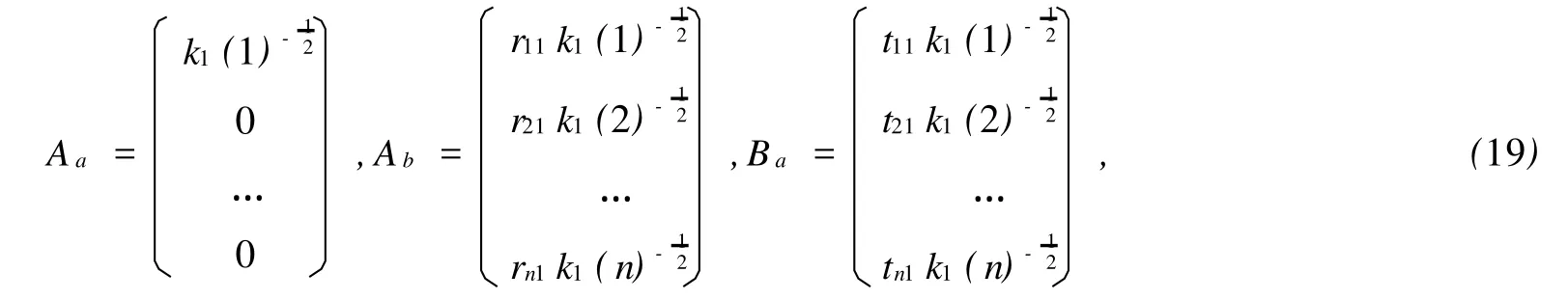
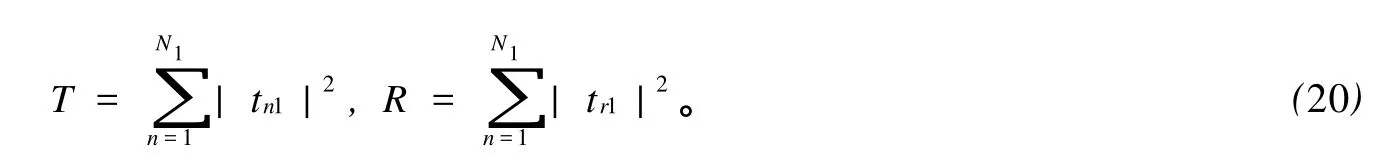
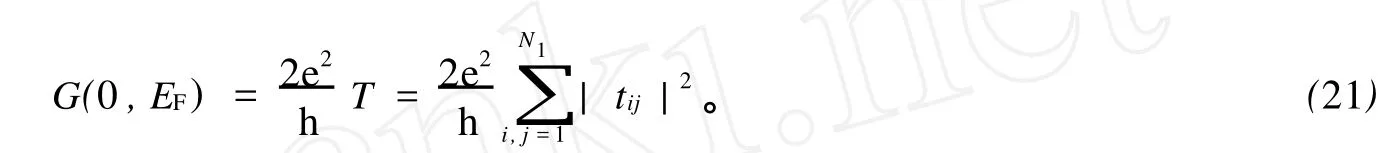
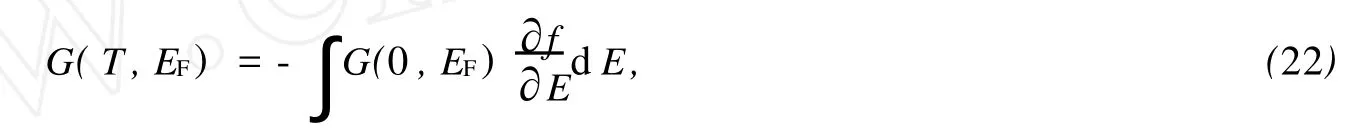
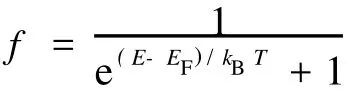
2 数值计算和结果分析

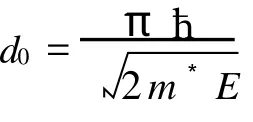
3 结 论
(College of Sciences,Hebei University of Science and Technology,Shijiazhuang Hebei 050018,China)
