Co50Fe50－xSix合金的结构相变和磁性*

赵晶晶 舒迪 祁欣 刘恩克 朱伟 冯琳 王文洪 吴光恒

Co50Fe50－xSix合金的结构相变和磁性*

赵晶晶1)2)舒迪1)祁欣1)刘恩克2)朱伟2)冯琳2)王文洪2)吴光恒2)

1)(北京化工大学理学院，北京100029)
2)(中国科学院物理研究所磁学国家重点实验室，北京100190)
(2011年1月28日收到;2011年4月20日收到修改稿)

利用实验测量和理论计算相结合的方法，研究了介于B2结构CoFe低有序合金和L21结构Co2FeSi高有序合金之间的Co50Fe50－xSix合金的结构相变、磁相变、分子磁矩和居里温度．采用考虑Coulomb相互作用的广义梯度近似(GGA+U)方法计算了合金的能带结构．研究发现，合金出现较强的原子有序倾向，表现出较强的共价成相作用．合金的晶格常数、磁矩、居里温度随Si含量的增加而线性地降低，极限成分Co2FeSi合金的分子磁矩和居里温度分别达到5.92μB和777℃．原子尺寸效应导致合金晶格发生变化，但并未成为居里温度和分子磁矩变化的主导因素．分子磁矩的变化符合Slater－Pauling原理，但发现原子磁矩的变化并非线性，据此提出了共价成相对磁性影响的观点．采用Stearns理论解释了居里温度的变化趋势，排除了原子间距对居里温度的主导影响作用．能带计算的结果还表明，Co2FeSi作为半金属材料并非十分完美，可能在实际应用中会出现自旋极化率降低的问题．发现该系列合金的结构相变和磁相变随着成分的变化聚集在窄小的成分和温度范围内．

磁性，Heusler合金，结构相变

PACS:71．20．Be，71．20．Lp，75．50．Bb

1.引言

L21结构的Co2FeSi在Heusler合金中具有最高的分子磁矩(6μB)和最高的居里温度(TC=1100± 20 K)［1］．2007年，Nakatani等［2］报道用考虑Coulomb相互作用的广义梯度近似(GGA+U)方法对Co2FeSi的电子结构计算，获得了与实验测量结果一致的分子磁矩6.0μB，并指出Co2FeSi合金具有半金属性，从而成为在磁电子学方面具有潜在应用前景的候选材料之一．因此，近年来对Co2FeSi合金的研究工作不断增多．研究Heusler合金磁性的有效方法之一就是对其中某种元素进行替代，观察一系列等结构合金的磁性、晶体结构和成相行为等物理性质的变化．替代的方式有的是在两种Heusler合金间替换转变，还有的是在Heusler合金与一种二元基体合金间的替代转变．CoFe是目前已知的具有最大分子磁矩的过渡金属二元合金，具有低磁晶各向异性和矫顽力、高磁导率和低剩磁等特性，其磁性和原子有序化问题在很多前期研究中都有所报道［3，4］．但从CoFe到Co2FeSi之间替代转变的角度，对Heusler合金Co2FeSi的研究目前尚未见报道．

为了从一个新的角度深入研究Co2FeSi的基本物理性质，寻找研究磁性-结构相关性的新出发点，本工作采用实验测量与理论计算相结合的方法，研究了B2结构有序合金CoFe经过Si替代Fe转变成L21结构Heusler合金Co2FeSi的一系列结构相变、磁相变、分子磁矩和居里温度(TC)等物理行为．研究发现，在Co50Fe50－xSix合金中随Si成分的增加，晶格常数、原子磁矩和分子磁矩、居里温度等物理参数有规律地单调变化;在晶体结构变化与磁结构变化纠缠在一起的窄小成分区间，出现了一些结构和磁性行为的异常;电子浓度的变化导致了Fermi能级的相对右移和交换作用的减弱;合金的态密度的变化造成了半金属性在实际应用中将出现低抗干扰的问题．本工作对这些现象给予了物理解释，并认为这些初步发现可以成为今后深入研究Co2FeSi合金的新出发点．

2 ．实验与计算方法

Co50Fe50－xSix系列多晶样品采用氩气保护的电弧熔炼方法制备，使用的金属纯度均大于99.9%．每个样品熔炼四次以保证成分均匀．熔炼后的合金样品密封在氩气保护的石英管中，在1000℃均匀化热处理48 h，考虑到CoFe合金在730℃附近有一个有序化转变［5］，所以在700℃将样品有序化热处理24 h后炉冷，以获得高度原子有序．用Cu靶X射线衍射仪分析样品的晶体结构，磁测量采用超导量子干涉器(SQUID)．用差热分析(DTA)方法测量样品的结构相变和原子有序化相变温度．由于CoFe合金发生自发磁化时伴有较强的比热变化［6］，因此，DTA测量也可以观察到系列合金的居里温度．为了突出DTA测量的效果，DTA测量中采取了适当增大样品质量(约为300 mg)和改善样品与坩埚导热接触的措施．电子结构的计算采用基于密度泛函理论(DFT)方法及考虑电子间Coulomb相互作用(U)的广义梯度近似(GGA)方法，即GGA+U，这里UCo= 3．0 eV，UFe=2.5 eV．在k空间中，平面波截止能选400 eV，k网格点为8×8×8，以保证体系能量和构型的收敛．

3 ．结果与讨论

CoFe合金为体心立方结构，空间群Pm3 m，Co原子占据A(0，0，0)位，Fe原子占据B(0．5，0．5，0．5)位．Co2FeSi是金属间化合物，呈L21结构，空间群Fm3 m．两个Co原子分别占据A(0，0，0)和C(0．5，0．5，0．5)位;Fe原子占据B(0．25，0．25，0．25)位，而Si原子占据D(0．75，0．75，0．75)位．本工作研究的对象是Co50Fe50－xSix(x= 0—25)系列合金，也就是在CoFe合金中用Si逐渐替代Fe，直至x=25时成为Heusler合金Co2FeSi．

图1 合金样品的粉末XRD图(a)CoFe;(b)Co50Fe34Si16; (c)Co2FeSi

粉末X射线衍射(XRD)方法可以确定合成的样品的结构，判断样品中原子占位的有序程度．在一些高有序的Heusler合金中，可以观察到(111)和(200)超晶格衍射峰，其中(111)峰代表B位和D位之间的原子有序，(200)峰代表A位、C位和B位之间的原子有序结构［7］．图1给出了CoFe，Co50Fe34Si16，Co2FeSi三种典型合金样品的粉末XRD图谱．可以看出，样品均为立方结构单相．CoFe合金的XRD谱中虽然没有出现超晶格峰，但从下面的测量结果可知的确是有序的B2结构，没有出现(200)峰的原因是Co和Fe原子的散射因子很接近［5］．在Si取代Fe后的Co50Fe34Si16样品中出现了(200)峰(见插图)，表明合金中Co原子有序占据在A和C位，而Fe和Si原子由于成分的缘故在B和D位无序占据，合金呈B2结构．随着Si原子的继续增加，合金变为Co2FeSi时，(111)和(200)两个超晶格峰出现，表明在正分成分中Fe和Si原子的占位是有序的，合金呈L21结构．因此，随着Si原子的增加，Co50Fe50－xSix系列合金逐渐从B2结构转变为L21结构．

通过拟合，我们得到Co50Fe50－xSix系列合金的晶格常数，如图2所示，两端的合金CoFe和Co2FeSi的晶格常数分别为0.5714 nm和0.5637 nm．在Fe逐渐被Si取代的过程中，晶格常数呈线性下降．这主要是因为Si原子的半径小于Fe的原子半径．线性拟合实验点，得到了理想的晶格常数的成分关系，并用于此后的能带计算中．

图3是Co-Fe二元相图［5］，从图中可以看到中间成分Co50Fe50(CoFe)合金随着温度的降低，在1476℃—985℃区间呈面心立方A1(αCo，γFe)相，在985℃发生从A1到体心立方A2相(αFe)的相转变．然后又在730℃时发生从A2相到B2(α')相的转变．其中A1相呈顺磁态，其TC低于A1-A2转变温度．CoFe的A2相呈铁磁性，但因其TC高于A1-A2相转变温度而不可测量．

我们已经知道，Co2Fe Z(Z为主族元素)基的Heusler合金在凝固过程中，可直接成体心立方相．而Heusler合金Co2FeSi实际上就是用Si替代CoFe合金中50%的Fe．因此，CoFe合金表现出来的A1-A2相转变，必将随着Si替代Fe量的增加，消失在某一Si含量的成分处．本工作采用DTA测量方法，研究了这一替代过程中的结构相变和磁相变行为．

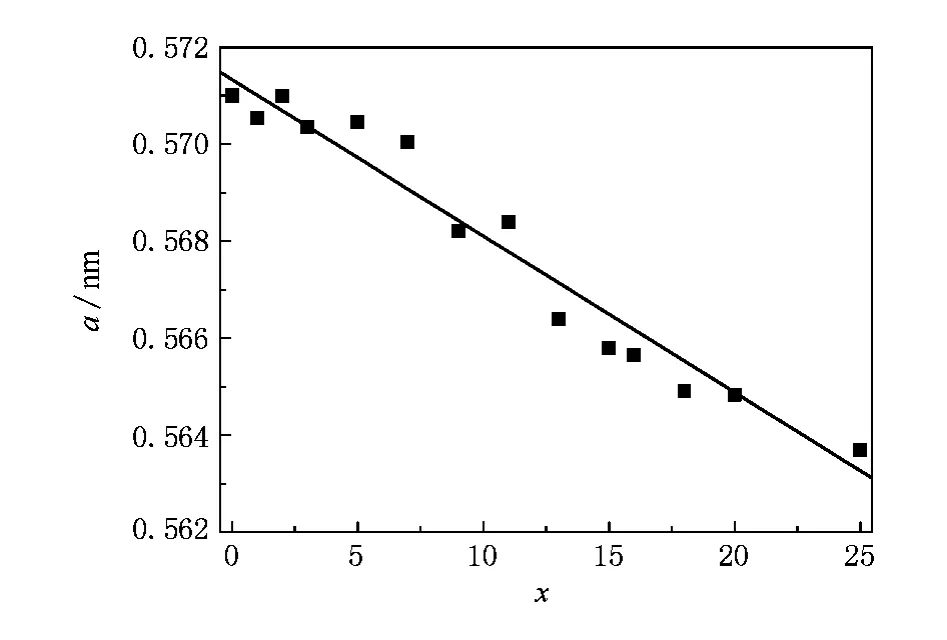
图2 Co50Fe50－xSix的晶格常数随Si含量的变化

图3 Co-Fe二元相图［5］

如图4(a)所示，在CoFe合金的DTA测量中观察到了在997℃和968℃出现两个明显的吸/放热峰，这对应于A1-A2相转变，伴随约30℃的热滞．由于这里叠加了A1-A2一级相变和顺磁-铁磁二级相变两个相变，因此相变峰很明显．考虑到测量设备和测量方法所产生的误差，可以认为与图3中的A1-A2相变温度是基本一致的．而发生在730℃和725℃的两个吸/放热峰属于CoFe合金A2-B2的有序转变，与相图所示一致．这两个热峰宽化程度并不严重，热滞也很小．这显示了这种材料的一个特征:A2-B2有序化相变虽然是原子扩散型一级相变，但进行得迅速而充分．

图4 合金样品(a)Co50Fe50，(b)Co50Fe38Si12，(c)Co50Fe34Si16，(d)Co50Fe25Si25的DTA变温曲线

当Si含量增加到x=12时，如图4(b)所示，Co50Fe38Si12合金的DTA测量分别在升温的945℃和降温的880℃，测量到了A2-A1的相变峰，其热滞增大到65℃．值得指出的是，在降温过程中，在出现A1-A2相变峰之前，观察到了在大约915℃出现的另外一个小的热过程．这对应于A1相的居里温度．这个磁转变在升温过程中没有观察到单独的吸热峰，可能的原因是由于A2到A1的一级相变温度滞后造成了结构相变与磁相变的重合，这可以从升温曲线的吸热峰更加宽化得到印证．这个样品的A2-B2的原子有序化相变用当前的测试方法已经无法观察到明显的热变化峰，其原因可能是凝固成相时，已经有部分B2相形成，而造成低灵敏度的DTA测量方法无法明显显示．在少量增加了Si含量至x =16时，如图4(c)所示，Co50Fe34Si16合金的DTA测量只在891℃出现了一个比较宽化的热峰，这对应着样品B2相的居里温度，但A1-A2相变的迹象则消失了．由此可以确定，CoFe合金原有的A1-A2相变，由于Si对Fe的替代，在Si成分为12≤x≤16之间的样品中消失了，说明这是一个临界成分区域，当0≤x≤12时，合金是B2相;当16＜x≤25时，合金逐渐趋向于L21相．

从以上结果可以看出，在12≤x≤16的Si成分范围中，出现了一系列值得注意的晶体结构和磁结构的变化．首先，原有的A1-A2的相变在此消失，样品直接成A2相;其次，A1相的居里温度(x=12时，TC=915℃)由于Si的替代而升高，出现在这个成分区间的样品中;第三，A2(B2)相的居里温度也在这个成分区间开始出现;第四，A1-A2相变出现了异常，热滞明显增大．需要特别指出的是，根据目前的测量结果，上述物理性质转变不仅聚集在一个窄小的成分区间，也有可能发生在一个窄小的温度范围(大约50 K)内．这种在接近相同的温度下出现的晶体结构相变和磁结构相变聚集的材料体系，以及结构和磁性的异常现象，为研究磁性对结构的影响提供了难能可贵的实验平台．有关研究结果将在后续工作中予以报道．

继续增加Si含量到x=25，从图4(d)可以看出DTA测量到我们合成的正分Heusler合金Co2FeSi的居里温度为777℃．必须指出的是，Heusler合金Co2FeSi的居里温度在以往不同文献报道中出现了从707℃(980 K)到827℃(1100 K)［1］很大范围的差异．一种解释认为，这与Co2FeSi中原子有序度有关［1］．但我们认为这也许与居里温度的测量方式和确定方式不同有关．例如，在文献［8］报道的热磁曲线中，若将磁化强度变化率最大的温度点定为居里温度，则为大约1055 K(782℃)，与本工作采用DTA方法测量到的居里温度基本一致．而本工作的热处理时间仅为48 h(1000℃)+24 h (700℃)，比文献［8］的20 d(1027℃)短得多，并且观察到了DTA测量中B2-L21转变不明显的事实．这意味着Co2FeSi的有序化成相水平是很高的．从中可以推测，原子间较强的成键作用(在本工作中是Co-Si，Fe-Si间的极性共价键作用)在Co2FeSi合金中较强．这部分的深入工作将采用更精确的示差扫描热量分析(DSC)和同步磁场中热重(TG)分析的方法，研究结果将在后续工作中予以报道．

当A1-A2相变消失后，Co50Fe50－xSix系列合金的自发磁化将从结构相变的掩盖中显现出来，使材料的居里温度得以测量．如图5所示，在16≤x≤25的成分区间，合金居里温度从Co50Fe34Si16的891℃线性地减小到Co2FeSi的777℃．以往对这类现象的解释，多采用非磁性元素(本工作中的Si)替代了磁性元素Fe的“稀释”作用，或者归因于“价电子”浓度的变化．我们认为，这些解释过于表面化，并未触及交换作用的本质．

Stearns针对磁性过渡金属合金和Heusler合金的交换相互作用所做的研究认为，过渡金属中3d电子除了大部分呈局域性(dl)外，还存在少量的巡游性(di)．dl和di电子之间的交换作用使di极化，而di电子的浓度主导了材料体系的磁交换相互作用［9，10］．Si原子取代Fe原子的成分增加过程中，Fe原子的浓度降低．使合金中di电子浓度降低．这就使得dl和di电子之间的交换作用减弱，导致了居里温度的降低．Stearns关于交换相互作用的理论指出di电子的自旋极化率随原子间距的增大而减小，而我们前面的结构分析指出，随着Si含量的增加，晶格常数是减小的．由此可知，在本工作的系列合金中居里温度的降低，与元素替代造成的原子间距变化无关，而主要是由di电子的浓度变化主导的．

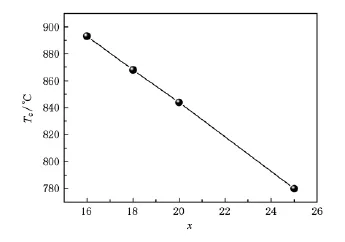
图5 Co50Fe50－xSix合金的居里温度随Si成分的变化

图6 所示为实验测量的Co50Fe50－xSix系列样品分子磁矩随成分的变化，并与能带计算的结果进行了对比．分子磁矩是根据5 K温度下测量的磁化曲线(见图6插图)计算所得．从图中可以看出实验值与理论值符合得很好，这也证明了计算方法和结果是可靠的．两个端点成分CoFe和Co2FeSi的分子磁矩分别为9.46μB和5.92μB，与前人文献报道的实验值一致［1，11］．由于我们考虑了电子间Coulomb相互作用，所以Co2FeSi的分子磁矩的计算得以与实验结果一致．此前一些计算工作中，如果不考虑Coulomb相互作用，Co2FeSi的分子磁矩计算值大约在5.72μB

［12］，与实验结果相差较大．考虑Coulomb相互作用时，原子磁矩之间的交换作用起源于电子之间的Coulomb相互作用［8］，本文关于Co2FeSi的计算考虑了Co，Fe原子电子之间的Coulomb相互作用，即更为精细地考虑了它们之间的交换作用，使得计算结果与实验值相符．

从图6可知，随着Si含量的增加，Co50Fe50－xSix的分子磁矩在整个替代过程中线性地下降了3.54 μB，符合Slater-Pauling原理，磁矩随着“价电子”浓度的降低而减小．计算显示，这种现象更本质的原因是，随着Si的成分增加，磁性原子3d电子的浓度降低，态密度发生变化，导致Fermi能级(EF)随着合金电子浓度的减小而相对右移(见图8)，这样就减弱了合金的磁性［13］．

图6 Co50Fe50－xSix系列样品的分子磁矩随Si成分的变化

Co50Fe50－xSix系列样品的分子磁矩随成分呈线性变化，但各原子磁矩随Si含量的变化却并非如此．图7给出了计算得到的Co50Fe50－xSix系列合金的磁矩随Si成分增加的变化．这首先说明Co50Fe50－xSix系列合金在Si含量的变化过程中Co和Fe原子磁矩都是铁磁性排列的．在Si替代Fe的过程中，Co的磁矩逐渐减小，从1.62μB降低到了1.36 μB，变化比较大，主导着分子磁矩的变化．而Fe原子的磁矩从3.12μB升高到了3.22μB，变化相对较小．

图7 计算得到的Co50Fe50－xSix合金的分子磁矩和各原子磁矩随Si含量增加的变化

从计算结果中可以看到合金中的分子磁矩呈线性变化，已经为实验结果所证实．而各个磁性元素的原子磁矩的变化则并非线性．这表明在元素替代的过程中，各个磁性原子的磁矩变化与分子磁矩变化并非主从关系，而Slater-Pauling原理仅仅是对分子磁矩变化的唯象解释．这更容易令人注意到分子磁矩的线性变化与Si(Fe)原子浓度线性变化的一致性，强共价作用导致了磁矩的降低［14］，而共价作用与Si原子数成正比，这很可能是分子磁矩线性变化的原因．

图8 计算得到的Co50Fe50－xSix合金的态密度(a)CoFe，(b)Co2Fe1．5Si0．5，(c)Co2FeSi

计算得到的三个典型的Co50Fe50－xSix合金的态密度如图8所示．－8 eV以下主要是能量较低的Si的s电子，它们受3d电子的影响很小，因此并没有在图中给出．在－8 eV到+2 eV之间的态密度峰主要来自过渡族元素的贡献，这与Co-Co，Co-Fe之间的强的共价杂化作用有关．在立方晶场的作用下，Co，Fe的自旋态密度发生eg－t2g能级劈裂，形成了低能的成键态峰和高能的反键态峰，之间由态密度较低的赝能隙隔开［15］．Co原子位上局域着很高的成键态密度并位于Fermi能级以下，无论是向上向下自旋都是如此．而在Fermi能级以上，随着Si原子的增加，Co原子的反键态密度减小，反键态峰能量也逐渐降低．同时，在－3 eV至－7 eV范围内，可以观察到Si与Co原子自旋向下的态密度存在明显增强的共振峰，而Si与Fe原子之间则未观察到这一现象，这表明Si与Co原子之间发生了较强的轨道杂化作用．这意味着Co原子与Si原子的成键使得其交换劈裂被削弱，导致Co磁矩的降低．在Fe的自旋向上的态密度中，成键峰和反键峰均位于Fermi能级以下，但在自旋向下的态密度中，由于交换劈裂的作用，反键峰被移到了Fermi能级以上的区域，这将使Fe具有较大的原子磁矩．由于Si与Fe原子无显著共价的键合作用，Fe原子的反成键态密度和反成键峰能量在Si含量增加的过程中基本不变，所以Fe原子的磁矩基本保持不变．

对Heusler合金Co2FeSi的研究工作最近几年不断增多，主要的原因是认为这种材料具有半金属性．但是，从上述的计算结果看，在这个材料中费米能级过于靠近导带底(图8(c))，即使其基态具有半金属性，但从实用角度考虑，其抵抗缺陷和热扰动的能力较弱［16］．这二者都可以造成传导电子自旋极化的大幅度降低．此前已经有报道采用在Co2FeSi中用Al部分替代Si，试图将Fermi能级移动到下旋能隙中间［2］．但是，这种方法容易引起原子无序化的问题，因为Al容易引起Fe-Al原子间B2类错占位［17］．本工作中Co2FeSi能带结构的计算结果指出了这个问题．这启发了我们采用新的能带设计的方法去获得更好的半金属CoFeSi合金，其结果将在后续工作中报道．

4 ．结论

本工作将实验测量与电子结构计算相结合，从B2合金CoFe经过Si替代Fe转变成L21结构Co2FeSi Heusler合金的角度，研究了Co50Fe50－xSix系列合金结构相变、磁相变、分子磁矩和居里温度等物理性质随成分的变化．研究发现:合金出现较强的原子有序倾向，表现出较强的共价成相作用;合金的晶格常数、磁矩、居里温度随Si含量的增加而线性地降低;晶格变化的原因是由原子尺寸效应造成．分子磁矩的变化符合Slater-Pauling原理，但计算结果指出，电子浓度机制很可能仅仅是一种唯象的解释．原子磁矩变化方式与分子磁矩相左的事实，更倾向于突出了共价成相的作用．能带计算中Fermi能级相对右移的结果，更进一步证实了这一观点的合理性．本工作采用Stearns理论解释了居里温度的变化，从而得出原子间距在该材料系列中居里温度变化不是主因的结论．能带计算的结果还指出，Co2FeSi作为半金属材料并非十分完美，可能在实际应用中会出现自旋极化率降低的问题，指出了设计新的材料体系的必要性．本工作发现，合金的结构相变和磁相变随着成分的变化聚集在窄小的成分和温度范围内，并呈现出相变滞后异常增大．这表明Co2FeSi有可能成为进一步研究磁性对晶体结构影响的有利对象．

［1］Wurmehl S，Fecher G H，Kandpal H C，Ksenofontov V，Felser C，Lin H J 2006 Appl．Phys．Lett．88 032503

［2］Nakatani T M，Rajanikanth A，Gercsi Z，Takahashi Y K，Inomata K，Hono K 2007 J．Appl．Phys．102 033916

［3］Eguchi T，Matsuda H，Oki K 1968 IEEE Trans．Magn．4 476

［4］Hanlumyuang Y，Ohodnicki P R，Laughlin D E，McHenry M E 2006 J．Appl．Phys．99 08 F101

［5］Okamoto H，Subramanian P R，Kacprzak L 2000 Desk Handbook Phase Diagrams for Binary Alloys(Vol．2)(Ohio:ASM International)p1186

［6］Dai D S，Qian K M 1987 Ferromagnetism(Vol．1)(Beijing: Science Press)p105(in Chinese)［戴道生、钱昆明1987铁磁学(上卷)(北京:科学出版社)第105页］

［7］Webster P J 1969 Contemp．Phys．10 559

［8］Huang K，Han R Q 1988 Solid State Physics(Beijing:Higher Education Press)p417(in Chinese)［黄昆、韩汝琦1988固体物理(北京:高等教育出版社)第417页］

［9］Stearns M B 1973 Phys．Rev．B 8 4383

［10］Stearns M B，Norbeck J M 1979 Phys．Rev．B 20 3739

［11］Buschow K H J，van Engen P G，Jongebreur R 1983 J．Magn．Magn．Mater．38 1

［12］Wurmehl S，Fecher G H，Kandpal H C，Ksenofontov V，Felser C，Lin H J，Morais J 2005 Phys．Rev．B 72 184434

［13］O＇handley R C 1999 Modern Magnetic Materials:Principles and Applications(Vol．2)(New York:A Wiley-Interscience Publication)p144

［14］Kübler J，William A R，Sommers C B 1983 Phys．Rev．B 28 1745

［15］Qi J S，Yu H L，Jiang X F，Shi D N 2010 Int．J．Mod．Phys．B 24 967

［16］Zhao J J，Qi X，Liu E K，Zhu W，Li G J，Wang W H，Wu G H 2011 Acta Phys．Sin．60 047108(in Chinese)［赵晶晶、祁欣、刘恩克、朱伟、钱金凤、李贵江、王文洪、吴光恒2011物理学报60 047108］

［17］Balke B，Fecher G H，Felser C 2007 Appl．Phys．Lett．90 242503

PACS:71．20．Be，71．20．Lp，75．50．Bb

*Project supported by the National Basic Research Program of China(Grant No．2010 CB833102)，the National Natural Science Foundation of China(Grant No．60971019)，and Specific Funding of Discipline and Graduate Education Project of Beijing Municipal Commission of Education．

Corresponding author．E-mail:qixin@mail．buct．edu．cn

Structural phase transition and magnetic properties of Co50Fe50－xSixalloys*

Zhao Jing-Jing1)2)Shu Di1)Qi Xin1)Liu En-Ke2)Zhu Wei2)Feng Lin2)Wang Wen-Hong2)Wu Guang-Heng2)
1)(School of Science，Beijing University of Chemical Technology，Beijing 100029，China)
2)(State Key Laboratory of Magnetism，Institute of Physics，Chinese Academy of Sciences，Beijing 100190，China)
(Received 28 January 2011;revised manuscript received 20 April 2011)

The structural and the magnetic properties of Co50Fe50－xSixalloys are investigated by carrying out experimental measurements and electron structure calculation．The alloy series exhibits the highly chemical ordering structure，showing a strong covalent bonding effect．The lattice parameters，molecular moment and Curie temperature linearly decrease with the increase of the Si content．The deviation of the structure is attributed to the atomic size effect．Based on Stearns theories，the decrease of the itinerant 3d(di)electron results in the decrease of Curie temperature due to the substitution of Si for Fe．The change of molecular moment follows the Slater-Pauling rule，but the calculation indicates that the change of the atomic moments is not linear．It implies that the covalent bonding effect is responsible for the magnetic changes．The molecular moment and Curie temperature of Heusler alloy Co2FeSi are measured to be 5.92μBand 777℃，respectively．The calculation results also indicate that the half-metallic property of Co2FeSi may not be so perfect as reported，which requires a new design of energy band for the practical application．The investigation also shows that the structural transition and the magnetic structure transition accumulate in a narrow interval of Si content，which may become a good object for studying the interaction between the magnetization and the structure．

magnetic properties，Heusler alloys，structural phase transition

*国家重点基础研究发展计划(批准号:2010 CB833102)、国家自然科学基金(批准号:60971019)和北京市教育委员会学科与研究生教育建设项目专项资助的课题．

．E-mail:qixin@mail．buct．edu．cn