基于ANSYS优化设计的JJ162/42-K型井架模型修正
2011-10-30彪周国强易
于 彪周国强易 俊
(1.重庆科技学院,重庆401331;2.大庆石油学院,秦皇岛 066004)
基于ANSYS优化设计的JJ162/42-K型井架模型修正
于 彪1周国强2易 俊1
(1.重庆科技学院,重庆401331;2.大庆石油学院,秦皇岛 066004)
有限元模型修正是指通过对有限元计算模型参数的识别和修正,建立反映结构实际状态的有限元模型,本质上属于优化问题。根据现场对JJ162/42-K型井架的实测模态数据,采用基于特征值灵敏度的优化设计方法对井架理想有限元模型进行修正。运用ANSYS软件计算目标函数和状态变量,优选出灵敏度较高的设计变量,采用合适的优化方法进行优化迭代,最后得到较为精确的有限元模型。
井架;有限元;灵敏度;优化设计;模型修正
井架的有限元建模是安全检测的重要步骤,有限元模型可以完整、直观地反映井架静态和动态特性。但有限元模型通常是按照设计蓝图建立的理想模型,其中隐含了多种理想化、假定和简化的条件。由于现场井架大部分已经服役多年,各构件、构件间联接及井架整体都有不同程度的损伤与缺陷,因此井架理想的有限元模态特性与实测的模态特性存在一定误差。研究井架模型修正技术可以使理想的有限元模型趋于实际井架的结构,反映井架结构的真实状态和实际工作性能,对于井架的健康检测和安全评估有重要意义。
利用现场实测的振动信息,对井架有限元模型进行参数修正,通过迭代过程,使得分析模态和试验模态之间的误差在给定的收敛边界内达到最小,即为有限元模型修正技术。本文根据实测的模态振动数据,采用基于特征值灵敏度的优化设计方法对JJ162/42-K型井架有限元模型进行修正,其研究结果可为井架检测和安全评估提供重要理论依据。
本文将理论与实际井架模型固有频率的相对误差作为目标函数,其振动方向为x-x和y-y的两阶固有频率作为状态变量,一些不确定的参数作为设计变量,运用ANSYS软件计算目标函数和状态变量,对设计变量进行灵敏度分析,优选出灵敏度较高的设计变量,采用合适的优化方法进行优化迭代最后得到较为精确的有限元模型。
1 模型修正方法
1.1 特征值灵敏度分析
将一连续结构体系离散为n个自由度的有限元模型,通过下列特征方程求解结构第n阶特征值λi:

其中刚度矩阵K和质量矩阵M由结构参数p决定。结构参数p包括各构件材料、几何特性、构件联结条件以及边界条件。因此,一定结构的模态参数是由结构参数决定的。特征值灵敏度分析一般采用直接求导的方式,将特征值视为结构参数的多元函数,直接对其求导而得出以某一参数为目标函数的灵敏度函数。
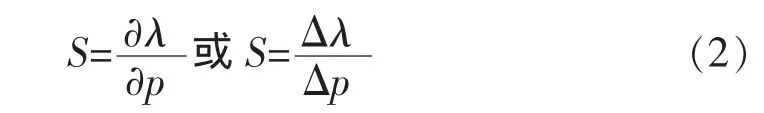
基于特征值灵敏度的参数选择方法,以灵敏度较高的参数作为有限元模型修正参数。值得注意的是,当有参数对测量值(频率)影响非常小,或几个参数对测量值影响相近时,灵敏度矩阵S常常呈现病态。另外,当待修正参数较多或实测数据存在较大误差时,修正的参数往往失去其物理意义。
1.2 模态相关性判断准则
理论模态和实测模态的相关性是用来判断理论模态和实测模态在一定准则上的相符程度。为了保证理论模态与实测模态的频率、振型相互匹配,在进行优化修正前,还必须分析原始模型与测试之间各阶模态的相关性。同时考察频率和振型的相关性可以提高模型修正的准确性。
(1)频率相关性分析。固有频率通常是动力分析的最基本参数,而且比模态振型向量更容易准确测量。实测频率ωt与理论频率ωa之间的相关程度常用下式来表示:

但是在某些频率非常接近的情况下,仅靠频率相关比较难以判断实测模态和理论模态之间的吻合程度。
(2)振型相关性分析。理论振型与实测振型的相关性可以通过模态保证准则MAC来计算:
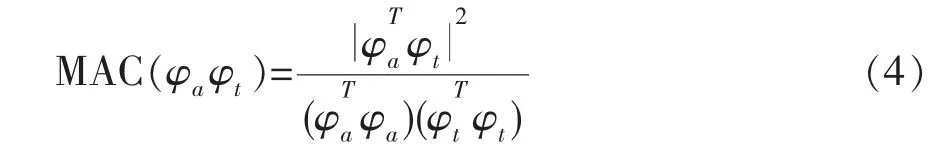
式中φa与φt分别代表理论与实测模态振型向量。如果模态完全相关,则MAC=1.0;如果模态完全不相关,则MAC=0。MAC值越接近于1,则表示理论模态与实测模态的相关性就越好。
1.3 约束优化原理
结构的有限元模型修正问题可以转变为结构参数的优化[4]问题。有限元模型的修正过程就是利用结构的实测动力特性(频率、振型等)进行参数优化的过程。
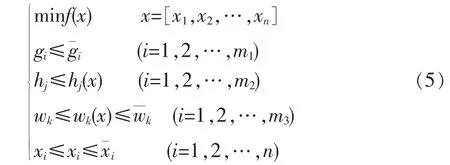
式中:f为目标函数;x 为设计变量;gi、hj和 wk为状态变量;m1、m2和m3为约束条件个数。使用一阶分析法将有约束多变量规划问题变为无约束规划问题,即将原目标函数f(x)增加罚函数变为新函数:
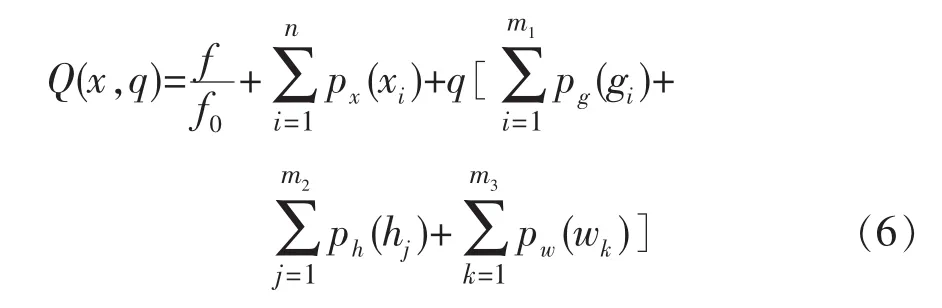
式中:f0为参考目标函数;q为控制约束参数;px为设计变量外罚函数;pg、ph和pw为状态变量混合罚函数。
1.4 收敛准则
迭代修正的收敛准则[5]定义为:
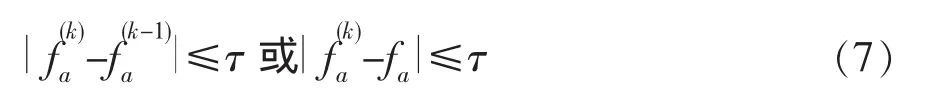
2 JJ162/42-K型井架理论与试验模态分析
2.1 JJ162/42-K型井架
大庆市三环钻井工程有限公司1003钻井队使用的是JJ162/42-K型井架(如图1所示),该井架高度42m,杆件材料均为Q235,弹性模量为2.06×1011Pa,泊松比为0.3,密度为7 850kg/m3。

图1 大庆三环1003钻井队ZJ25D钻机
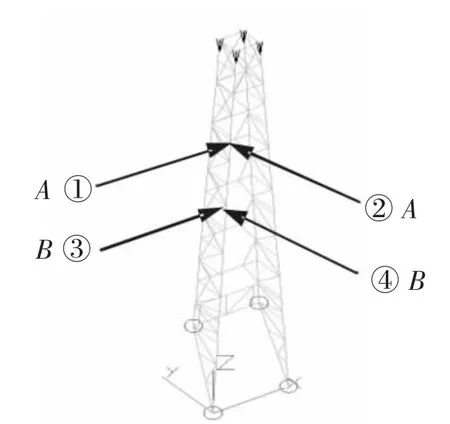
图2 振动测点布置图
2.2 井架动力测试
井架在环境载荷激励下通常只有几个低阶模态能够较精确地测量到,因此模型校正也应当主要通过校正低阶模态来完成。布置测点数量及测点位置如图2所示。其中立柱共布置2个水平x-x向参考点以及2个垂直向y-y参考点。
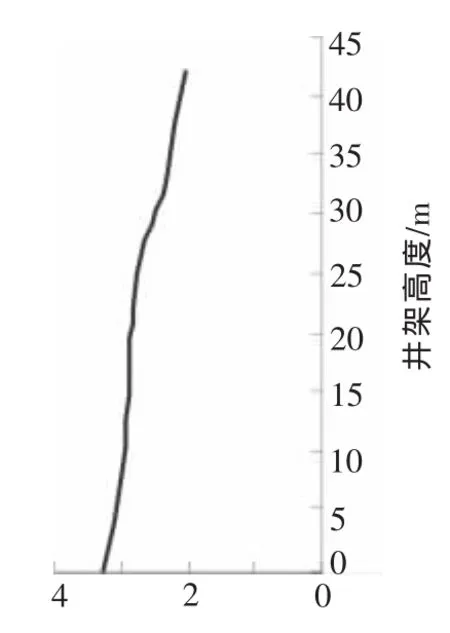
图3 井架y-y向一阶振型识别结果
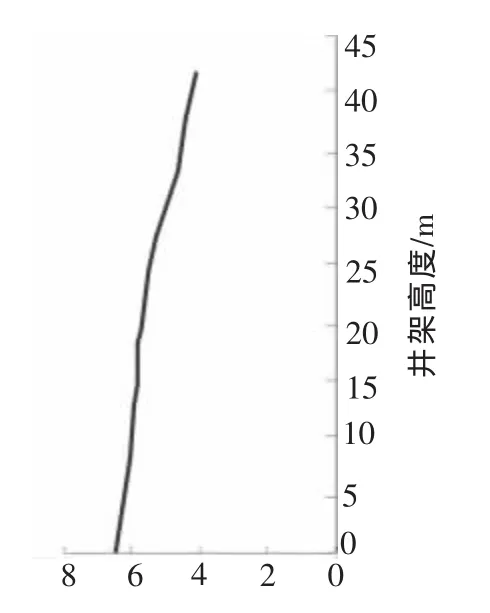
图4 井架x-x向一阶振型识别结果
井架模型动态信号通过布置在井架大腿上的加速度传感器拾取,由ZonicBook振动测试系统采集,最后通过eZ-Analyst软件对测试信号进行处理和分析。得到实测频率,x-x方向振动频率1.313,y-y向振动频率为1.375,振型识别如图3、图4所示。
2.3 有限元分析
构造JJ162/42-K型井架空间有限元分析模型(图5所示),采用大型有限元通用软件ANSYS,按照实际尺寸,对底座上部结构进行建立。将二层台、天车、工作梯和人字架等附件在简化时全部忽略,二层台和天车的质量视为集中质量分配于相应的结点位置。井架各杆件均承受轴向力和弯矩作用,各结点均视为焊接的刚性结点,故将其简化为空间刚架结构。计算时采用有限元方法,将井架各杆件简化为梁单元进行有限元离散,共80个节点,178个单元。 根据实际位置施加约束,对井架支柱脚节点和人字架支撑点施加x,y和z方向的约束,模拟实际的固结状况。
用ANSYS软件的模态计算模块对其进行特征值分析,得到其前四阶频率频率(如表1)及计算振型(如图5所示)。
3 JJ162/42-K型井架的有限元模型修正
3.1 模态参数理论与实测结果比较
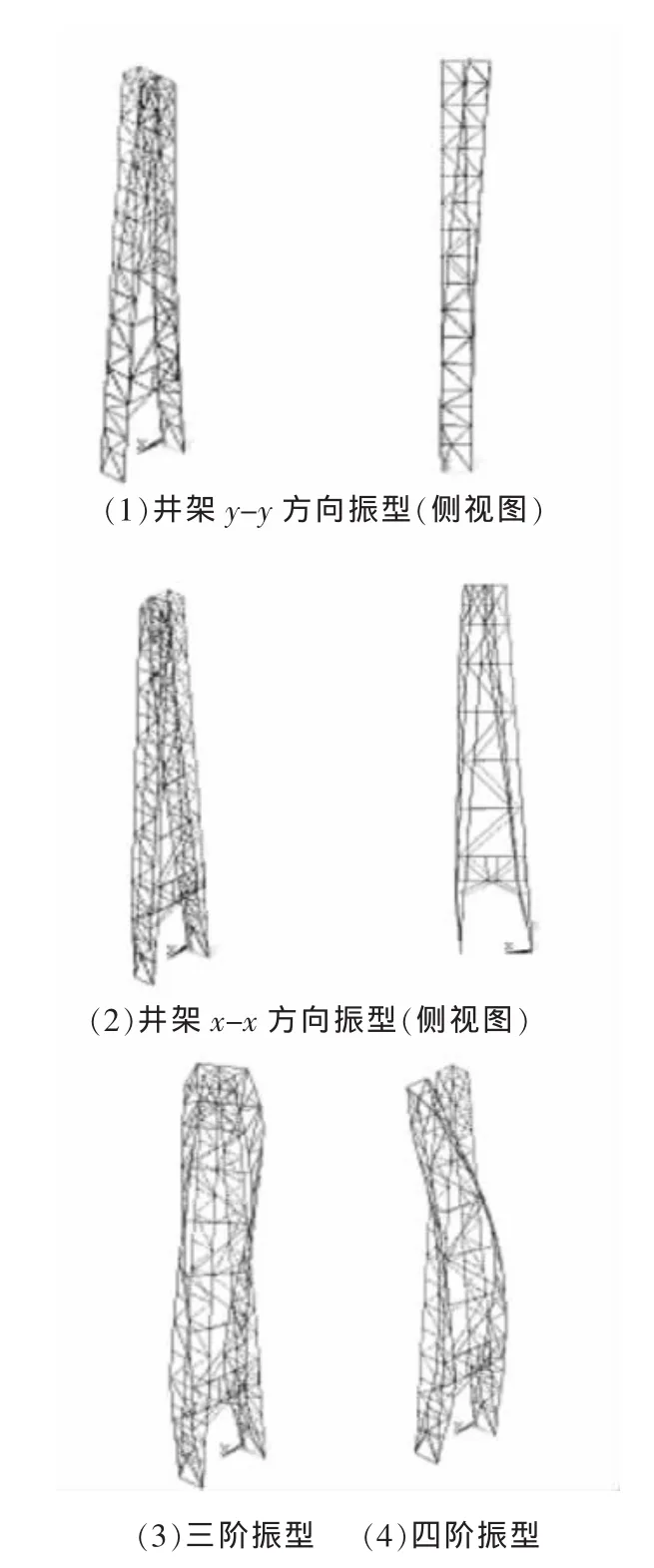
图5 井架振型图
由于理论有限元模型的振型次序与实测结果并不一致,为了保证计算模态与测试模态的频率和振型相互匹配,在进行优化修正前,首先将理论振型和实测振型“配对”。利用MAC准则来定量地检验实测与理论模态参数的相关性,MAC为1或接近1,说明两振型相关性好,或者说是同振型。通过振型配对得到相应的理论和实测振型对,由表2可以看出,理论与实测振型具有较好的相关性,但理论与实测频率具有一定的差异。

表1 井架模型前四阶频率 Hz

表2 实测和计算频率相关性
3.2 待修正结构参数的选择
在井架的模型中,由于模型主要是采用梁单元建立的,所以可供选择修正的参数较少,首先根据建模和经验,可以作为模型修正的参数包括弹性模量、质量密度和各作为杆件截面的几何性质。但依据图纸,三种圆形钢管作为结构的辅助支撑对井架整体结构影响相对较小,并且根据实际情况现场井架质量密度是不会改变的,因此可以不予选用。弹性模量作为整体结构的参数是会随着整体结构及连接的变化而发生变化。其次通过灵敏度分析和几次的优化设计结果可以看出,角钢L的截面几何性质对井架频率的影响相对于弹性模量和箱型梁而言非常的小,可以忽略。综合以上分析,可将井架弹性模量、箱梁厚度以及纵向和横向长度4个参数作为井架模型的修正参数。最后确定的待修正参数及其初始估计值列于表3。
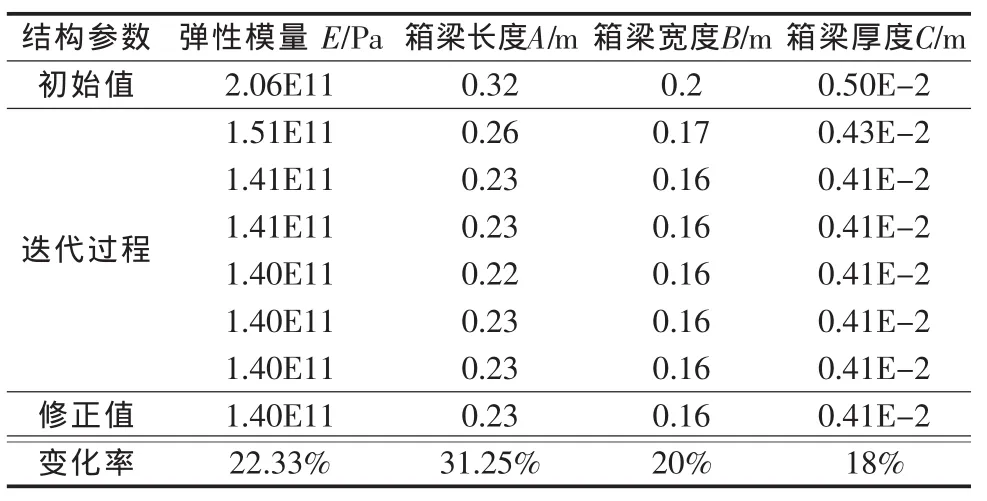
表3 实验室井架修正前、后的参数值及其变化
3.3 模型参数的修正
对初始有限元模型进行特征值敏感参数分析,可知弹性模量E、质量密度M及截面积A对所有的振型和频率都有影响,截面惯矩Izz、Iyy及Ixx则只对特定的振型产生影响。依据迭代收敛准则,对初始有限元模型进行逐步修正(见图3),经过迭代后理论与实测频率收敛到准则允许误差范围内,最大误差为3.8%,最小误差为0.2%。迭代后的理论有限元频率见表5,结构参数的修正值见表4。
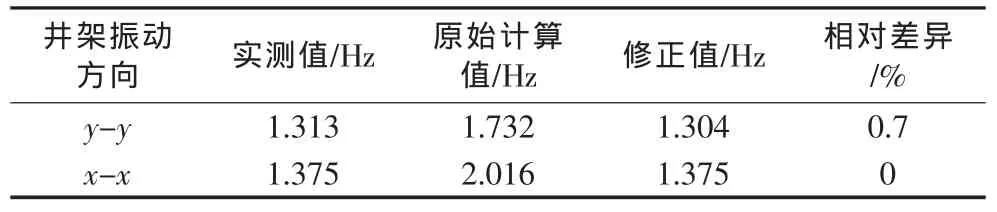
表4 井架模型修正前、后的频率值及其变化
4 结 论
采用基于特征值灵敏度分析的优化设计方法,以实验室井架实测的模态分析结果为依据,对建立的理想有限元模型进行优化修正。结果显示该方法可以较好地修正初始建立的实验室井架模型,使得理想有限元模型大大逼近于实际结构,反映井架结构的真实状态和实际工作性能,从而为井架的检测和安全评估提供更加准确的理论有限元模型。
[1]范立础,袁万城,张启伟.悬索桥结构基于敏感性分析的动力有限元模型修正[J].土木工程学报,2002,33(1):9-13.
[2]马雪洁.基于ANSYS的桁架优化设计[J].焦作大学学报,2004(4):22-23.
[3]张启伟.桥梁结构模型修正与损伤识别[D].上海:同济大学,1999.
[4]严云.基于ANSYS参数化设计语言的结构优化设计[J].华东交通大学学报,2004,21(4):52-55.
[5]夏樟华.基于静动力的桥梁结构有限元模型修正[D].福州:福州大学,2005.
On Optimization Design of Type JJ162/42-K Derrick Based on ANSYS
YU Biao1ZHOU Guo-qiang2YI Jun1
(1.Chongqing University of Science and Technology,Chongqing 401331;2.Daqing Petroleum Institute,Qinhuangdao 066004)
Updating finite element(FE)model is something of optimization.The purpose of model updating is to identify and correct uncertain parameters of FE model,which can lead to the better predictions of structural real dynamic and static behavior.In accordance with the modal data obtained from field tests of the model of Type JJ162/42-K Derrick,the optimization design principle based on the structural sensitivity analysis was used to update the ideal finite element model of the derrick.The results reflect the true state of derrick structure and actual work performance.
derrick;finite element;sensitivity;optimization design;model updating
TE925:TE319
A
1673-1980(2011)06-0100-04
2011-08-29
于彪(1982-),男,黑龙江齐齐哈尔人,硕士,研究方向为井架及长输管道检测。
