基于多目标规划的会议筹备模型设计
2011-10-28李亚男
李亚男
(肇庆科技职业技术学院,广东 肇庆 526114)
基于多目标规划的会议筹备模型设计
李亚男
(肇庆科技职业技术学院,广东 肇庆 526114)
针对2009年全国大学生数学建模竞赛D题——“会议筹备”中的有关数据进行综合分析,以选择的宾馆数量最少、宾馆间距离上最靠近为两个目标函数,同时考虑与会代表在价位、是否独住两方面的约束,通过采用多目标规划进行问题建模并求解来制定一个预定宾馆客房的合理方案。
数学建模;曲线拟合;多目标规划
1.问题的提出及分析
针对2009年全国大学生数学建模竞赛D题[1]——“会议筹备”中如何制定预定宾馆客房的合理方案的问题,综合考虑经济、方便、代表满意等方面来建立优化模型,具体主要从与会代表的价位需求、所选宾馆的数量和距离来分析,采用多目标规划进行问题建模与求解。
2.模型的建立与求解
2.1 数据的处理
首先根据问题提供的数据信息来估算与会的代表的人数。
设x为发来回执的代表数量,y为发来回执但未与会的代表数量,Z为未发回执与会的代表数量,根据题中附表3的信息且利用Matlab软件[2]的曲线拟合可以得出x与y的函数关系为:y=0.2995x +0.4592。用此函数拟合的效果如图1所示:
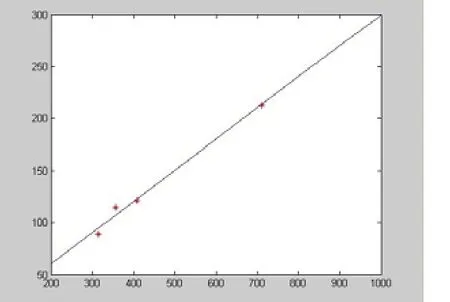
图1 发来回执但未与会的代表数量与发来回执的代表数量之间的曲线拟合图
也可得出x与z的函数关系为:z=0.1094x +27.4212。曲线拟合如下图(图2):

图2 未发回执与会的代表数量与发来回执的代表数量之间的曲线拟合图
利用题中附表2的信息可计算出本届发来回执的代表数量为755人,利用上面所得出的拟合函数,可估算出本届发来回执但未与会的代表数量为:
0.2995 ×755+0.4592≈227,
本届未发回执而与会的代表数量为:
0.1094 ×755+27.4212≈111,故本届与会代表的数量可估算为:755−227+111=639。
根据附表2由此可以估算与会代表有关住房要求的信息(单位:人),如下表(表1):

表1 与会代表人数及需要的房间数
2.2 模型的分析
假设xij为需要第i号宾馆第j种规格的数量(比如需要1号宾馆普通双标间的数量记为x11),xi为需要第i号宾馆的房间总数,yi为0-1变量,表示第i号宾馆是否被预订,若被预订则为1,否则为0。即
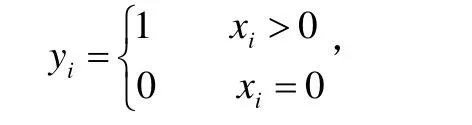
由于预计会议规模庞大,而适于接待这次会议的几家宾馆的客房和会议室数量均有限,所以只能让与会代表分散到若干家宾馆住宿。结合实际,主要制定合理的预定宾馆客房的方案,以满足两个需求因素:目标1:选择的宾馆数量最少;目标2:宾馆间距离上最靠近。
目标分析:
在保证选择的宾馆数量尽可能少的同时,对距离也要求比较靠近。
目标1可表示为:

根据题中附图可统计出10间宾馆各间宾馆之间的乘车距离,如下表(表2):

表2 各宾馆间的乘车距离(单位:米)

为了满足距离上最靠近,可考虑入住宾馆各间之间的距离之和达到最小。
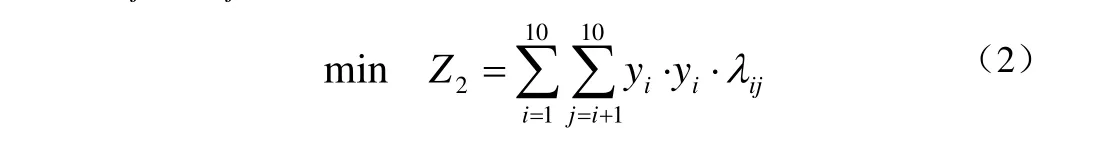
约束分析:
与会代表回执中不仅对每间住房有价格上的要求,而且也同时要求合住或独住。价格上分每天每间120~160元、161~200元、201~300元三种不同的价格,合住是指要求两人合住一间,独住是可安排单人间,或一人单独住一个双人间。
因此,在安排住房时,应先考虑双人合住的数量。故有如下约束:
①合住1和独住1满足的总房间数

其中,xij为需要第i号宾馆第j种规格的数量。
2.3 模型的建立与求解
基于2.2的分析,以(1)(2)为目标,以(3)~(8)为约束,建立多目标规划模型,其求解可采用多属性效用函数,将多目标规划模型转化为单目标规划模型来求解。
首先,考虑到模型中的2个目标函数都是要求最小化,因此运用线性加权法将多目标规划模型化为单目标规划模型来求解,加权得到的优化模型如下所示:

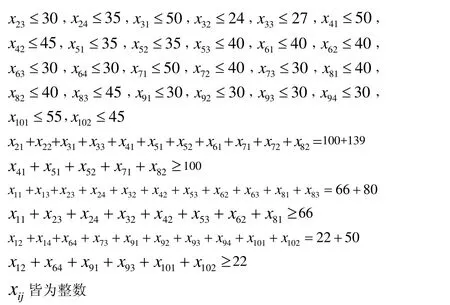
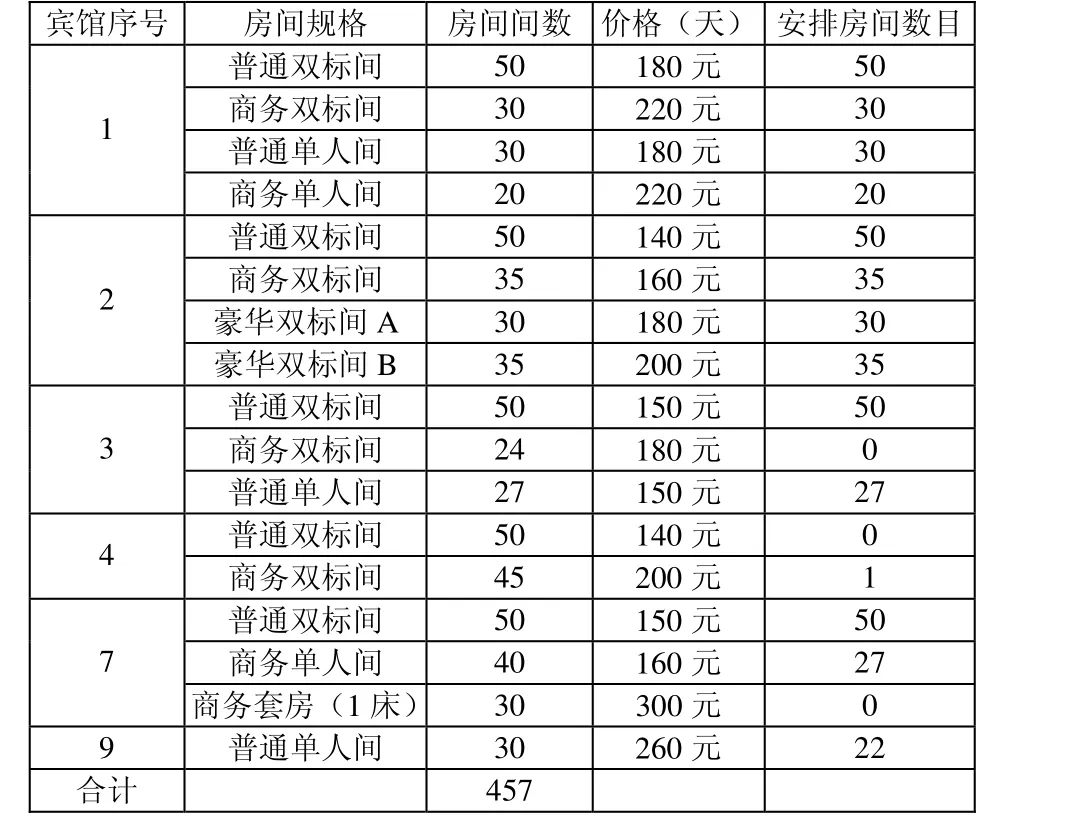
表3 各宾馆预订房间信息
从上表容易看出,共需要安排6间宾馆住宿,为1、2、3、4、7、9号。有些宾馆需要的客房数量很少,可考虑调整其它有入住代表的宾馆内,使得宾馆数量尽可能减少。由于4号宾馆只安排了1间房,根据题中附表2的价位范围可调整至3号宾馆商务双标间中;同理,9号宾馆中22间房可移至7号商务套房(1床)中。通过调整,得到结果如下表(表4):识比较明确,这反映了大学生体育认知水平的提高,也与经济的发展和社会的进步有着密切关系。但仍有近3成的女生对体育锻炼的意义认识不清,这就需要体育教育工作者不断加强对学生的体育意识教育,正确地开发和引导她们的体育动机,努力促使她们养成自觉锻炼的良好习惯。

表4 各宾馆预订房间信息(调整后)
2.5 影响学生参加课外体育活动的主要原因

表5 主要原因分析
调查结果显示表5:影响大学生课外体育活动的主要原因依次为:无时间、无器材、无场地、无兴趣、无人指导、怕受伤、不会练、体弱多病、家长反以对等。“无时间”是主要影响因素,无器材、无场地、无兴趣为次要因素,大学生可以通过自身的调节和消除次属原因,使保持良好的健康水平。
3.结论与建议
3.1 结论:(1)我校约有80%的学生能够不同程度的参加课外体育活动,大部分学生体育锻炼意识和习惯正在形成。(2)学生课外体育活动的动机几乎都是健康积极的,希望通过体育锻炼增强体质,丰富自己的业余生活和社会交往。
(3)学生课外体育活动的主要场所是本校体育场馆和宿舍,主要是以球类为首选项目,课外体育锻炼的形式以个人锻炼为主。(4)场地、器材与学生数相比,严重不足,这在很大程度上影响了学生参与课外体育锻炼。
3.2 建议:(1)强化学生进行体育锻炼的意识,通过体育理论的讲授使学生掌握体育独特的培育人的过程。(2)加大学生课外体育活动的组织与管理,教师应加强对学生进行科学体育锻炼的指导,提高锻炼的效果。(3)应根据学生的喜好,抓一个重点运动项目,形成学校体育特色活动,带动课外体育锻炼。(4)学校应充分利用现有的场地设施,挖掘潜力,加强管理,延长开放时间,提高场馆的利用率。
[1] 张兰,张胜志,等.甘肃省普通高校大学生课外体育活动现状调查[J].体育科学,2004,3.
[2] 曾吉.普通高校学生课外体育活动的调查研究[J].浙江体育科学,2000,12.
After- school Activities Of Our Students For Investigation And Analysis
BAO Hai-li
This paper made a thorough investigation on the students attitude about participating in sports activities, activities forms, the frequency and sports facilities as well as their other favorite items, through the methods of questionnaire surveying and document data, aims to provide reference for the development of our school sports activities.According to the surveying of the current situation on the students participating in sports activities after school at the Institute of Navigation, Marine Engineering College, Port Administration, marine tourism college, and puts forward the corresponding suggestions based on the existing problem.
physical activities after-school; investigation; present situation
O221.6
A
1008-7427(2011)04-0154-02
2011-03-04
