大学生关于学习的混沌认知的调查研究
——以邯郸学院为例
2011-10-26董春华席改卿郑新芳任宁
董春华 席改卿 郑新芳 任宁
邯郸学院化学系,河北 邯郸 056005
大学生关于学习的混沌认知的调查研究
——以邯郸学院为例
董春华 席改卿 郑新芳 任宁
邯郸学院化学系,河北 邯郸 056005
为了解当代大学生混沌认知特点及其与学业成绩间的关系,对被试进行了关于学习的混沌认知的调查。结果表明:被试混沌认知水平在某些层面存在差异性,并且与学业成绩具有相关性。针对实际情况,就如何提高混沌认知水平提出了建议。
大学生;学习;混沌;调查
引言
混沌理论是二十世纪的三大科学革命之一,它与相对论、量子论并驾齐驱。混沌理论主要包括:蝴蝶效应、分形自相似性、奇异吸引子。混沌理论对教育界的冲击为人们提供了全新的视角[1,2]。
大学生作为高等教育的主体,是未来社会的栋梁。大学生面临诸多问题,其中最主要的是由中学生到大学生的角色转变。另外一个是由非专业到专业化的转变。在这个过程中,能否客观地认识自己,能否较快地适应,关乎大学生的自我成长,甚至关乎其职业生涯的走向。
为了探讨大学生混沌认知的特点和水平,及其与学业成绩间的可能存在的关系,我们进行了大学生关于学习的混沌认知的调查研究。
1 方法
1.1 被试的选择
本研究选择了河北省内新建地方本科院校邯郸学院化学系一年级学生作为被试,对其进行问卷调查。发放问卷166份,回收有效问卷137份。有效回收率为82.5%。
1.2 测试材料
根据研究的目的和思路,参考台湾屏东教育大学苏素增硕士论文《国小校园危机管理之研究——以混沌理论为例》[3],结合研究内容,拟定学习认知调查问卷。问卷共分三部分。第一部分主要记录被试的基本资料,包括六方面:分别是性别、专业、层次、生源地、曾任职务、政治面貌;第二部分考察被试者对学习的整体认识观,共有5个项目;第三部分考察被试者的学习的混沌认知水平。问卷采用李科特5点评分,记分从1~5分别是从“非常不赞同”到“非常赞同”,要求被试判断项目所描述的内容与自己的符合程度。按照问卷设计,问卷得分越高,表明具有对教学系统的整体认识观水平越高,混沌认知水平也越高。
本研究对学习混沌认知问卷进行了信度分析。混沌认知包括19个项目,分为四个维度。整体信度为0.810。P-P图检验基本呈正态分布。蝴蝶效应8个项目,信度为0.639。奇异吸引子4个项目,信度为0.505。反馈机制3个项目,信度为0.566。分形自相似性4个项目,信度为0.743。Cuieford[4]认为,若Cronbach α大于0.7,则具有高信度,若Cronbach α介于0.35~0.7之间为可接受信度;若Cronbach α小于0.35,则为低信度。以上数据表明学生问卷整体信度较高。
1.3 结果的统计
全部数据都采用SPSS 15.0进行统计,主要分析方法有描述统计、t检验、方差分析、相关分析、多元线性回归分析等[5,6]。
2 结果与分析
2.1 大学生对学习整体认识观的特点
对学习的整体认识观包括5个项目。分别是:教学系统开放性、学习过程非线性、学习动态性、学习结果非预测性、教学非因果决定论。
按李科特5点式分析可得:教学系统开放性得分2.61,认知程度偏低。学习过程非线性得分2.80,认知程度偏低。学习动态性得分3.85,认知程度一般。学习结果非预测性得分2.97,认知程度偏低。教学非因果决定论得分3.27,认知程度偏低。学习整体认识观平均分为3.1,认知程度一般。以上情况说明,目前学生作为学习的主体,对学习的整体认识不容乐观,认识还比较模糊。
2.2 大学生混沌认知的特点
2.2.1 均值比较。描述统计发现:混沌认知四个维度(蝴蝶效应、奇异吸引子、反馈机制、分形自相似性)及总体得分折算成李科特5点式可分别得4.11,4.57,4.65,3.89,4.25。分形自相似性认知属中上水平,蝴蝶效应认知、奇异吸引子认知、反馈机制认知、混沌总体认知属良好。其中分形自相似性认知亟待提高。
2.2.2 性别比较。描述统计发现:男生与女生混沌认知得分折算成李科特5点式可分别得4.06与4.35,总体属良好。独立样本t检验结果发现:男生与女生混沌认知差异显著,sig = 0.000<0.05。女性大于男性。蝴蝶效应认知差异显著,sig =0.001<0.05。女性大于男性。奇异吸引子认知差异显著,sig = 0.018<0.05。女性大于男性。反馈机制认知差异显著,sig =0.000<0.05。女性大于男性。分形自相似性认知差异显著,sig =0.039<0.05。女性大于男性。结果说明,女性比男性在混沌认知及各维度上具有更高的水平。这或许与被试女性的生理特点有关。一般认为女性对外界事物感知更敏感、细腻。
2.2.3 专业比较。描述统计发现:化学、应用化学、应用化工技术、化学制药技术专业折算成李科特5点式可分别得4.34,4.17, 4.17,4.28。各专业均属良好。化学专业得分最高,应用化学专业得分最低。单因素方差分析发现:混沌认知在专业上无显著差异。这说明由于被试为大学一年级新生,专业课程来不及全面开展,其特征也就不被赋予更多的专业色彩。
2.2.4 层次比较。描述统计发现:本科和专科折算成李科特5点式可分别得4.23,4.25。本科和专科都属良好。独立样本t检验分析发现:混沌认知在层次上无显著差异。这说明被试在基础教育阶段获得的学习认知总体差异不大。
2.2.5 生源地比较。描述统计发现:城镇和农村折算成李科特5点式可分别得4.15,4.25。城镇和农村都属良好。独立样本t检验分析发现:混沌认知在生源地上无显著差异。这说明被试家乡来自于城镇或是农村引起的学习认知差异不大。
2.2.6 曾任职务比较。描述统计发现:学生、课代表、学习委员、其他干部折算成李科特5点式可分别得4.06,4.19,4.43,4.36。学生、课代表、学习委员、其他学生干部混沌认知都属良好。学习委员得分最高,学生得分最低。单因素方差分析发现:混沌认知在曾任职务上有显著差异,Sig.= 0.004<0.05。事后比较法确定:学习委员大于学生,Sig. = 0.010<0.05 。蝴蝶效应认知在曾任职务上有显著差异,Sig.= 0.004<0.05 。事后比较法确定:学习委员大于课代表,Sig. = 0.019<0.05 。学习委员大于学生,Sig. = 0.024<0.05。反馈机制认知在曾任职务上有显著差异,Sig. = 0.002<0.05 。事后比较法确定:学习委员大于学生,Sig. = 0.003<0.05。以上结果表明,在学习认知上,学习委员由于其职务角色与学习的密切性,更多地显示出与其他同学的差异。
2.2.7 职业兴趣匹配比较。为了了解新生的职业兴趣状况,我们进行了霍兰德职业兴趣匹配程度的调查。为了认识职业兴趣匹配程度与学习认知水平间的关系,又进行了二者间的比较。描述统计发现:将霍兰德职业兴趣匹配与否的学习认知情况折算成李科特5点式可分别得4.31,4.22。均属良好。独立样本t检验结果发现:职业兴趣匹配与否在混沌认知上无显著差异。这说明二者之间属于两大不同的范畴,关联度不大。
2.3 混沌认知与学习成绩相关分析
通过研究被试的无机化学理论成绩及无机化学实验成绩与混沌认知的关系,发现以下特点(见表1,表2):
混沌认知与学习成绩逐步回归:
数据表明,混沌认知对学习成绩有明显影响。以理论后测成绩作为因变量,以混沌认知作为自变量,蝴蝶效应、奇异吸引子、分形自相似性进入回归方程,可以得出标准回归方程为:理论后测成绩 = 0.207 蝴蝶效应 + 0.353奇异吸引子 + 0.141 分形自相似性。通过β系数可以看出蝴蝶效应、奇异吸引子、分形自相似性得分越高,理论后测成绩则越好。
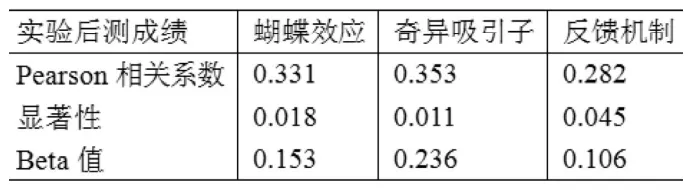
表2 混沌认知与实验后测成绩比较
以实验后测成绩作为因变量,以混沌认知作为自变量,蝴蝶效应、奇异吸引子、反馈机制进入回归方程,可以得出标准回归方程为:实验后测成绩 = 0.153 蝴蝶效应 + 0.236 奇异吸引子 + 0.106 反馈机制。通过β系数可以看出蝴蝶效应、奇异吸引子、反馈机制得分越高,实验后测成绩则越好。
3 结论
3.1 被试大学生对学习的整体认识观程度一般,尚需改进。
对事物本身能客观科学的认识是把握事物的基本前提,学习过程也不例外。调查发现,被试大学生对学习的认识水平不容乐观。通过跟踪研究发现,学生越往后两极分化越严重。在这个过程中,教师能否及时发现、有效干预其不良行为至关重要。例如发现有厌学症倾向的学生,应及时沟通、疏导,弄清症结所在,治标治本,帮助其进入良性循环。
3.2 被试大学生在混沌认知上不同性别、曾任职务存在显著性差异。
其中女性比男性认知水平高。学习委员比其他学生认知水平高。针对这种情况,可以专门对男性设计一些以小见大的训练,通过夸张的放大效应,加强认识。另外,学习委员任用可以采取轮换制,通过更多学生的自身体验使混沌认知水平提高。
3.3 被试大学生混沌认知水平与学习成绩存在正相关关系。
其中无机化学理论课后测成绩、无机化学实验课后测成绩与混沌认知水平均呈正相关关系。需要说明的是,以上结论是基于被试的数据分析,至于其他类型院校的学生尚需进一步研究。
针对实际情况,我们可以通过混沌认知的三大原理(蝴蝶效应、分形自相似性、奇异吸引子)的应用,完善学生的知识体系。首先:尝试开展拓展训练。模拟职场,预见未来,认清不足。通过这项活动,将学业与职业无缝对接。低年级学生往往不能切实地感知专业知识的重要性。通过实战演练,学生会意识到这不是试卷中的一道题目,得分高低无所谓,而是关系到一份工作的合约。通过超前的感知,学习变得不再空洞。其次:积极与高年级学长沟通。同龄人的亲切感可以消除隔膜,他们鲜活的正反实例会更能触动心灵,帮助树立“我也行”的信心。再次:邀约成功校友经验谈。通过励志的演讲,讲述学业与职业的关系、成功路上的艰辛,激发参与挑战的热情。这样,学生通过自我的反思、同龄人的移情、成功人士的启迪使思想升华,夯实基础,锻炼意志,实现由小我到大我,由自我价值的实现到服务他人、回报社会的飞跃。
[1] You, Y. What can we learn from chaos theory? An alternative approach to instructional systems design [J ]. ETR&D, 1993; 41(3):17~ 32.
[2] 袁德明. 混沌式教学设计与实践[J].中国教育信息化.2007(8):66~68
[3] 黄希庭, 张志杰. 心理学研究方[M].北京:高等教育出版社.2005
[4] 甘怡群,等. 心理与行为科学统[M].北京:北京大学出版社.2005
[5] 苏素增. 国小校园危机管理之研究——以混沌理论为例[D].台湾屏东教育大学硕士论文.2007
[6] Cuieford, J.P. Fundament statistic in psychology and education[M].New York:McGraw Hill.Cuieford, 1965
Study on the Survey of College Students’ Learning Chaos Recognition——A Case Study of Handan College
Dong Chunhua Xi Gaiqing Zheng Xinfang Ren Ning
Department of Chemistry, Handan College, Handan, 056005, P. R. China.
In order to find out the characteristic of modern college students’ chaos recognition and the relation between chaos recognition and their studies’ achievement, a survey on study was carried out. It was found that there existed differences in chaos recognition and it had correlation with studies’ achievement.According to actual circumstance , suggestions are given on how to improve chaos recognition.
College students;Learning;Chaos;Survey
10.3969/j.issn.1001-8972.2011.08.153
河北省教育科学“十一五”规划课题“混沌理论在化学教学中的应用”(项目编号:08110024)。
董春华(1973-),女,邯郸人,硕士,邯郸学院化学系讲师,研究方向:无机化学。
