利用动态规划求解资源分配问题的单表迭代法
2011-10-26宋占岭冀秀春炮兵指挥学院河北宣化075100
宋占岭 冀秀春 炮兵指挥学院,河北宣化 075100
利用动态规划求解资源分配问题的单表迭代法
宋占岭 冀秀春 炮兵指挥学院,河北宣化 075100
将用动态规划求解资源分配问题时的各阶段迭代表格进行统一集成,利用基本方程递推关系式在同一表格中进行迭代,层次清晰,结果直观,利于计算机编程实现。
动态规划;资源分配问题;迭代法
动态规划是运筹学的一个重要分支,它是解决多阶段决策过程最优化的一种数学方法。这一方法最初是由美国数学家贝尔曼(R. Bellman)等人在20世纪50年代提出的。它根据多阶段决策问题的特点,把多阶段决策问题变换成为一系列相互关联的单阶段决策问题,然后逐个加以解决。动态规划的核心是最优性原理,即无论过去的状态和决策如何,对前面的决策所形成的状态而言,余下的诸决策必须构成最优策略。动态规划在工程技术、企业管理、工农业生产及军事等领域中都有广泛的应用,并且取得了显著的效果。实践证明许多问题用动态规划求解比用线性规划或非线性规划更加有效,特别是对离散性问题,运用解析数学无法解决,而动态规划就成为得力的工具。
1. 资源分配问题的动态规划模型
资源分配问题亦称投资问题,其一般提法如下:
设总投资额为a万元,拟投资于几个项目上,已知对第i个项目投资xi万元,收益函数为gi(xi)。问应如何分配资金才可以使总收益最大?
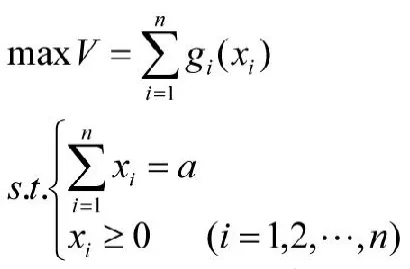
当gi(xi)为线性函数时,它是一个线性规划问题;当gi(xi)为非线性函数时,它是一个非线性规划问题。为了应用动态规划方法求解这类静态规划问题,可以人为地赋予它“时段”的概念,将投资项目排序,假想对各个投资项目有先后顺序。首先考虑对项目1的投资,然后考虑对项目2的投资,依次最后考虑第n项投资,这样就把原问题转化为n阶段的决策过程。把问题中的变量xi作为决策变量,将累计的量或随递推过程变化的量设为状态变量。
状态变量sk表示第k阶段可用于第k个到第n个项目的资金数,显然有s1=a,sn=0。
决策变量xk即应分配第k个项目上的投资额。
状态转移方程 sk+1=sk-xk。
最优指标函数fk(sk) 表示当可投资金数为sk时,投资于剩余的n-k+1个项目的最大收益。则基本方程为
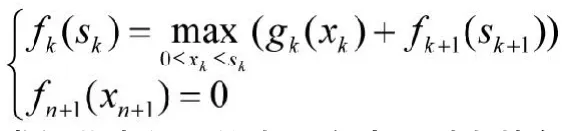
求解此类问题的常用方法是列出其各阶段投资决策收益表,利用基本方程递推关系式进行逐级迭代,最后求得f1(a)即为所求问题的最大收益,我们称之为“多表迭代法”。下面以文献[1]213页例1介绍之。
问题描述:某工业部门根据国家计划安排,拟将某种高效率的设备五台,分配给所属的甲、乙、丙三家工厂,各厂获得这种设备之后可以为国家提供盈利如表1所示。问这五台设备如何分配给各厂,才能使国家得到利益最大。

表1
建立模型后,其基本方程为
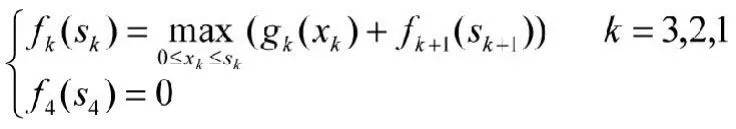
多表迭代求解过程如下:
k=3时,数值计算如表2所示。
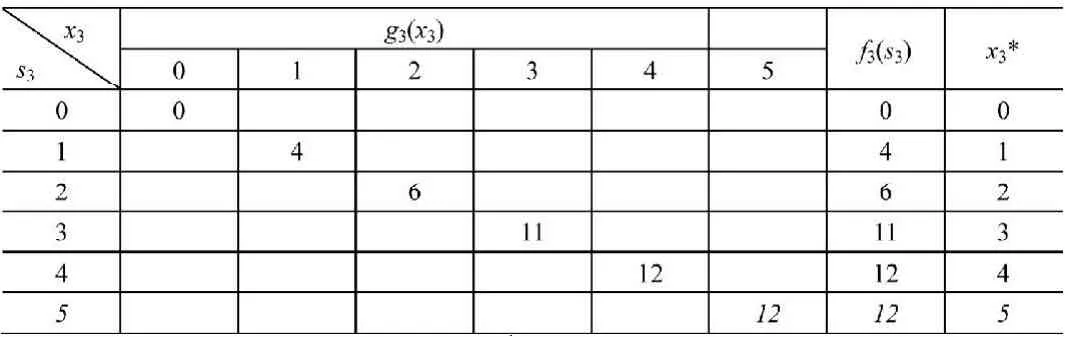
表2
k=2时,数值计算如表3所示。

表3
k=1时,数值计算如表4所示。

表4
最后按计算表格顺序反推,可知最优分配方案有两个:甲、乙、丙三厂分别分配0、2、3台及2、2、1台,均达到总盈利最大为21万元。
多表迭代法原理清晰,直观明了,但模型中有几个阶段就要列出几个表格,然后利用表格数据进行反复迭代,显得有些繁琐,不便于计算机编程实现。为此,笔者将各阶段表格进行统一集成,利用基本方程递推关系式在同一表格中进行迭代,以利于计算机编程实现,称之为“单表迭代法”。
2. 单表迭代法
单表迭代法计算步骤为:
(1)求出各阶段最优指标函数值,存放于迭代表中;
(2)将各阶段每一可能状态条件下的各指标函数与下一阶段的最优指标函数交叉相加后寻优,同时标出最优路径;
(3)根据最优路径确定最优决策。
前述问题求解结果见表5。
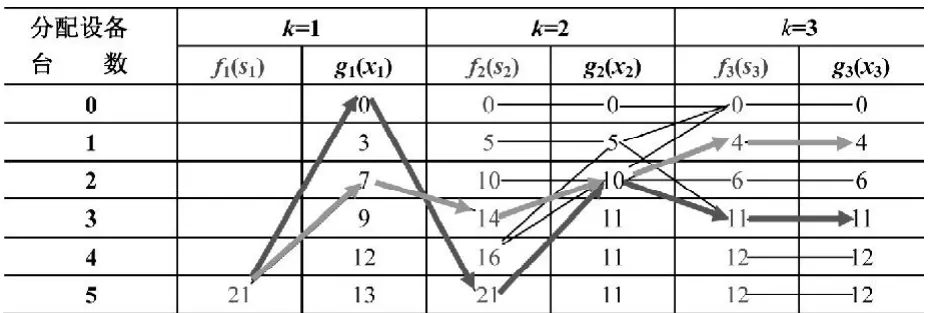
表5
单表迭代法在求解较大规模的问题时,具有很大的优越性。表6中的投资分配问题中,有6个单位的资源和4个方案,各方案在不同投资额条件下收益不同(具体数值参见表6),建立模型后,其基本方程为

用单表迭代法求解获益最大的投资结果见表6 。
由表6中迭代结果可知,此投资问题的最大收益为220个单位,共有5个最优方案可实现之。
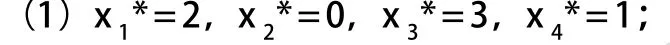
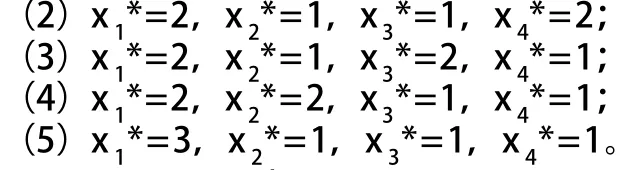
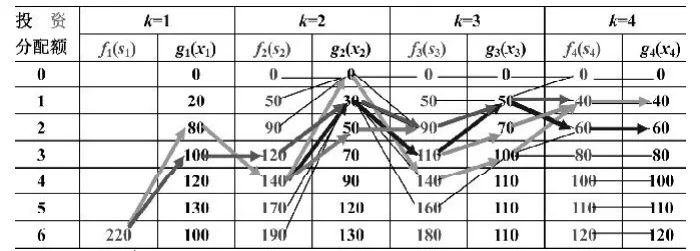
表6
3. 结论
利用动态规划求解资源分配问题的“单表迭代法”将“多表迭代法”的多个表格统一集成为一个表格,所有迭代计算都在同一表格中进行,层次清晰,结果直观,更便于计算机编程实现。单表迭代法对于顺序递推基本方程以及最优取最小值的资源分配问题同样适用。
[1] 运筹学教材编写组. 运筹学(第三版)[M]. 北京:清华大学出版社.2001
[2] 张野鹏. 军事运筹基础[M]. 北京:高等教育出版社.2006
10.3969/j.issn.1001-8972.2011.10.028
作者信息
宋占岭(1968—),男,河北宣化人,硕士;研究方向:军事运筹学。
