关于离心泵最优化设计理论与方法的研究

2011-10-26刘克伟贾月梅赵秋霞太原理工大学力学系太原030024

中国科技信息 2011年9期

刘克伟贾月梅赵秋霞太原理工大学力学系，太原 030024

关于离心泵最优化设计理论与方法的研究

刘克伟贾月梅赵秋霞太原理工大学力学系，太原 030024

本文分析了离心泵优化设计中的问题，由此提出了以自适应进化网格技术为核心，集自动化造型技术、CFD技术、最优化计算技术于一体的离心泵最优化设计理论与方法(最优化设计计算技术)。阐述了最优化设计理论的基本思想、离心泵自动化造型技术及算法、二维自适应进化网格及算法，基本上形成了这项技术的体系结构，从而使离心泵的优化设计有了新发展。

优化设计；自适应进化网格；离心泵；最优化设计理论

1、最优化设计理论及计算技术概述

本文致力于研究新的理论、方法和技术，解决离心泵优化设计问题。目前，离心泵节能优化已是备受关注的问题。现在，主要有两种方式优化离心泵。一是，采用CFD软件优化设计，例如fluent。但是这些软件只适合最终的检验，有些问题还不能解决，这正是CFD与其他学科交叉发展的必然结果。另一种方法是，用半经验半理论公式优化离心泵参数。这种方法也存在很多问题。笔者认为，应采用整机优化的方式，应在三维形状基础上用CFD计算水力损失较准确，应以总效率最高为目标，其他的目标函数均有些失真。而且应以单目标为宜（两相流除外），多目标函数对工程人员来说，权系数不好把握。汽蚀、驼峰列入约束条件为好。另外，叶轮进口参数受到很多限制不应优化，应由设计者凭经验给定。叶片数被优化的范围不应过宽。这样被优化的参数只有叶轮出口参数、叶片数和蜗壳参数（同一叶轮，考虑到互换性，不同的压出室按蜗壳优化，特殊情况下不按蜗壳优化）。自动化造出形状以后，用具有自适应进化网格的CFD技术计算总效率，再用最优化算法寻优计算。如果在优化过程中蜗壳的自变量保持不变，只优化叶轮参数，叶轮参数确定后再分别优化叶轮与蜗壳，这是可行的。需要输入程序中的参数有：叶轮进口直径、轮毂直径、叶片流道中线进口直径，叶片数范围，叶片类型（圆柱、扭曲）、叶片布置（是否长短叶片）、泵类型（单、多）、叶轮类型（单、双）、轮毂直径、叶片进口冲角范围、叶片进出口厚度、最大厚度、最大厚度位置、叶轮出口直径范围、出口角范围、出口宽度范围、滑移系数范围、前盖板厚度、后盖板厚度、叶轮与泵体轴向间隙、口环类型、口环间隙、长度、粗糙度、有效直径、叶轮与泵体粗糙度、叶轮与泵体径向间隙、蜗壳类型（单、双）、断面类型（分类型输入不同的几何参数）、第八断面面积、隔舌圆角半径（默认2.5mm）、隔舌安放角、出口扩散段类型（侧向、中间等）、泵出口直径、出口段扩散角范围、吸入室损失、其他容积效率损失（均压孔、平衡盘、级间泄漏）、其他机械效率损失、泵的流量、扬程、转速等。这些参数大多被程序初始化。这些参数就是最优化设计理论和方法需要的参数。

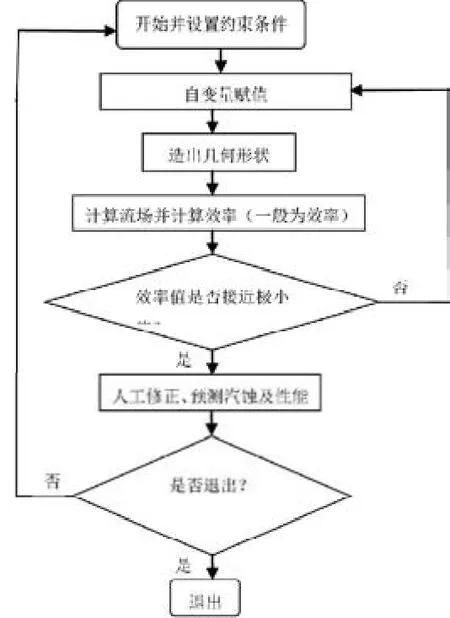
图1 最优化计算技术流程图

现简述离心泵最优化设计理论和方法—最优化设计计算技术。也可叫做整体最优几何形状求解法。整体最优几何形状求解过程是约束最优化计算过程，它集CAD、CFD、最优化理论及算法等多种计算技术于一体。首先，确定各个过流部件参与寻优计算的几何参数。对于蜗壳以第八断面面积和断面几何参数共同组成寻优自变量，叶轮为出口参数（详见上文），合理确定自变量范围，建立单目标函数（以总效率最高为目标，汽蚀、驼峰列入约束条件，两相流除外），根据初始几何参数由CAD技术自动化造型，再用CFD三维自适应进化网格技术计算流场并计算总效率，根据其值用最优化算法改变自变量值，重复以上步骤不断寻优计算直到解出最优几何形状为止。解出的最优几何形状有时并不是最好的，例如自动化造出的叶轮叶片在特殊情况下由于几何参数不良，造成叶片形状不太好，这时有必要对几何参数进行人工修正。如果修正过大，重复以上过程，再求解几何形状。此后还要进行性能和汽蚀预测，如不符要求调整自变量约束条件重新计算。这些过程很复杂，涉及多种计算方法，这就是离心泵优化设计的理想方法。计算机求解的是整个离心泵过流部件的几何形状。离心泵过流部件CAD自动化造型基本上尚属空白但完全可以实现（本文作分析），三维自适应进化网格有待进一步研究（也可实现），最优化计算方法十分成熟。这种计算技术能否应用关键在三维自适应进化网格和计算量。目前，计算机的计算速度相对这样的计算量还较慢。但在并行机上运行程序没有困难。可以说，这种技术一旦成为现实，离心泵的设计手段，乃至整个流体机械的设计手段再不会有太大的发展空间。算法流程图如图1。

2、自动化造型计算技术的研究

在Autocad中，利用objectarx二次开发实现最优化计算技术比较方便。Objectarx与Autocad共享地址空间，运算速度快。特别是它的AcGe类,这个类专门用于几何计算。用到的类有：AcGeCircArc3d、AcGeCircArc2d、AcGeTol等等，共29个。所有变量都定义成double型，由于是反复计算这些变量都定义成公共变量。

对于叶轮，自动化造型技术主要包括以下算法：后盖板流线等分点算法、内切圆算法、包络线算法、过流断面形成线算法、过流断面面积算法、排挤系数算法、前盖板流线自动生成算法、分流线算法、流线分点算法、进口边位置算法、叶片型面算法、叶片加厚算法，曲面缝合算法等。这些算法的细节会在专门文献中讨论。导流壳的自动化造型技术类似于叶轮，比叶轮要简单。叶片的生成较容易。下面简单叙述梯形蜗壳的自动化造型技术。

梯形蜗壳按照如下的过程自动化造型。根据流量、速度计算第八断面面积。按文献[1]的计算法绘制计算各断面形状。绘制第八断面时要考虑到泵出口直径，若梯形断面有一部分在出口圆之外时，调节断面两侧直线的γ角，直至在其内为止。若该角超出范围程序报错。若符合要求，再按照输入的γ角不变或按H*tan(γ)成等差数列变化两种情况（H 为一高度），同时按输入的隔舌安放角（是初始值，最后由计算机修正）计算各断面面积及形状。计算扩散管水力损失（半经验半理论公式计算），在扩散角允许的范围内得出最佳扩散角，扩散管即定型。按照输入的隔舌圆角半径（默认值2.5mm）修正隔舌安放角，再按照输入的γ角不变或按H*tan(γ)成等差数列变化两种情况（H 为一高度），按修正的隔舌安放角计算其余断面形状。这样蜗壳形状就确定了。以上是侧向出口的情况。出口在中间或其他位置，将扩散管去弯取直，按直锥管处里，其余同上。对于双蜗壳将面积扩大后，按一般蜗壳处理。其余类型的压出室造型较简单，不再详述。关于叶轮形状的优化方法，会在专门文献中讨论。下面借蜗壳的优化方法，说明自适应进化网格计算技术。自适应进化网格是在最优化理论控制下流场边界不断变形，高效率的反复计算流场的方法，以最优方案下的网格为演变目标。

3、蜗壳二维优化计算方法的理论基础

假定蜗壳内同一过流断面上各点水力损失相等及均匀化。可以证明螺旋段对称面水力损失变化趋势与整个蜗壳螺旋段水力损失变化趋势相同。可认为矩形蜗壳对称面流动属二维流动。可按二维方法优化蜗壳。优化时忽略扩散管段。优化其他断面形状蜗壳时，先按矩形蜗壳优化第八段面面积，然后按此面积设计非矩形蜗壳。详细证明过程见文献[2]。详细步骤类似于最优化设计理论的步骤（见下文）。

4、网格的自适应进化算法

4.1 网格的自适应

本文讨论一种快速自适应方法。图2中A为隔舌处，C点在第八段面上，BC为过流断面形成线。圆弧AC直径为基圆直径D3。为了使方法带有通用性需全面考虑边界形状。

第一步，离散边界。按以下步骤进行：①识别不同线段和尖角点。如图2中A、B、C点。这些点是不同线段的连接点，也就是导数不连续点。在objectarx中读取线段的起点和终点的坐标值就可以确定尖角点位置了；②识别光滑曲线上最弯曲处的点（如是直线不识别）。搜索出边界上曲率最大值的点即可（用AcGeCurve2d的样本点函数较方便，再用AcGePointOnCurve2d读曲率值比较）；③外边界和内边界的识别。如果有一条封闭环，就是外边界。如果有多条封闭环，找出包含其他封闭环的封闭环即可确定外边界的曲线（用AcGeNurbCurve2d的面积函数）。如果没有应报错。如果有判定其他封闭环是否相交（AcGeCurveCurveInt2d），如果相交报错。这一步为网格生成做准备；④边界的离散。在每条线上分别离散。如有弯曲最大处的点，这时将同一曲线分成若干个曲线。在每个曲线上分别离散。用样本点函数比较方便，给定弦高误差0.005mm，得到一系列离散点。利用此函数弯曲大的地方点就多一些，当两点间曲线距离大于最大距离时（给定边界离散点最大距离），按最大距离等分。当小于最小距离时合并。对于边界有导数不连续点的情况，按给定的两点最短曲线距离（三角形单元最小边长△lmin）离散这段边界。按此间距，被离散的边界曲线长度SL1按下式计算：

其中θ1和θ2分别是这条曲线段的起点和终点对应的尖角角度。若这条曲线有一端连接进出口边，上式中应去掉一项。若这条曲线段长度SL减去SL1的值小于等于2△lmin将整个曲线段等分或不分，点间边界曲线段长度按下式计算：

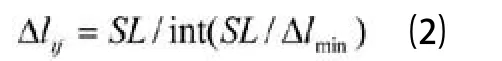
其中int()为取整函数。若长度SL减去SL1的值大于2△lmin，等分SL1后,按前述方法,按没有导数不连续点的情况离散剩下的这段曲线；⑤边界离散点的优化。目的是使点间距变化均匀适应边界曲线曲率的连续性变化。设某条曲线段起点0、终点n,函数X( )计算两点间边界曲线长度（用length()函数）。按下式迭代：

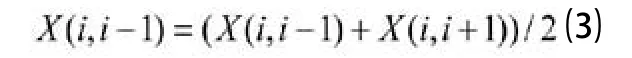
计算时从i等于1开始，计算三遍后停止。若有尖角的曲线段长度SL减去SL1的值小于等于2△lmin，这段曲线段不优化。最大弯曲处点、起点、终点位置不动。对于两点间距大于最大间距的分裂，小于最小三角形最小边长的合并。

第二步，网格生成。用objectarx中的boundBlock()函数生成计算域的外接矩形并在其中心插入一水平放置边长为Lm（给定三角形单元最大边长）的正三角形。以这个三角形边为边，顶点为顶点，生成新的同样边长的正三角形，每个节点均有六个同样边长的正三角形，以此类推，正三角形不断向四周生长，直到覆盖整个外接矩形为止。删除不在计算域内的节点及其所在三角形（包括边界上的）。删除离边界距离小于等于2△lmin的节点及其所在三角形。将边界离散点按Delaunay三角化方法一一插入并维护边界完整性，并优化网格。

第三步，网格的加密。本文进口边不加密。先判定三角形单元是否在加密区域。设三角形单元节点离边界距离为ZE。按下式判定三角形单元是否在加密区域（只需一个节点满足条件即可）：

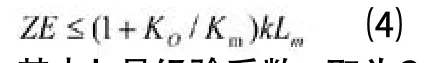
其中k是经验系数，取为2，KO是边界曲线上离该节点最近的点的曲率, Km 给定最大曲率。如果这个最近点是尖角点，KO=Km。若在直线上KO=0，若三角形在加密区域，再判定三角形是否符合加密条件（最长边大于给定三角形单元最小边长的2倍）。若符合加密条件，在其形心处插点。加密时，先搜索在加密区的所有三角形，确定所有插入点位置，然后再将这些插入点按Delaunay三角化方法一一插入。检查新生成的所有三角形单元是否符合加密条件，若符合继续加密，直到没有可加密的三角形单元为止。

第四步，三角形单元的收缩和优化。经上一步后可能有的三角形单元边长最小值小于给定最小值△lmin的0.95倍，这种情况下，需将此三角形收缩。如果此三角形的三个顶点均不是边界点，将此三角形收缩于形心O，也就是说，将三个顶点及所在三角形删除，O用Delaunay三角化方法按新节点插入。如果有一个是边界点，此三角形收缩到这个边界点A，

将三个顶点及所在三角形删除，A按新节点插入。如果有两个边界点，删除三个顶点及所在三角形，将这两个边界点按新节点插入。如果三个点都是边界点，不加密。最后用Laplacian光顺方法反复迭代优化。优化过程中边界点位置不变。

图2 计算平面及边界离散示意图

4.2 网格的进化

求解过程中以旧方案网格（有时不是上一方案）为基础，生成新网格。

第一步，离散新方案的边界并确定旧方案边界上网格节点的位移。首先，根据新方案的边界形状，由前述方法离散边界。根据旧方案边界节点的无量纲相对坐标值，将这些旧方案边界节点一一映射到新方案边界上。新旧方案边界形状有相似性，尖角点相同。新方案边界形状用更新旧方案曲线数据的方法生成。尖角点就一一映射了。对于边界上的急剧弯曲处的点有时新旧方案不能对应（不同时存在），如果同时存在可将这些点一一映射，如果不同时存在，根据旧方案边界节点的无量纲相对坐标值，将这些旧方案节点映射到新方案边界上。边界上其余节点按无量纲相对坐标值一一映射。如下图所示点C的无量纲相对坐标值为AC曲线段长度与AB曲线段长度的比值，或者是BC曲线段长度与AB曲线段长度的比值。图中A、B、C、D映射成A＇、B＇、C＇、D＇。这样旧方案边界网格节点的位移就给定了。

图3 映射法示意图

第二步，用修正的弹簧近似法重新生成网格。弹簧劲度系数按下式计算[4]：

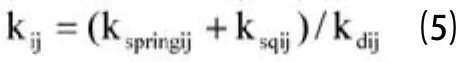
其中kdij为i、j两点中至边界最短距离的最小值。kspringij计算公式：

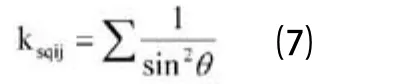
上式中Sminij为拥有网格边ij的所有单元中面积最小的单元面积。当Sminij→0时,Kspringiij→∞. 这样就保证了与网格边ij相对的所有单元中面积最小的单元不会成为面积为负的“无效”网格。lij为单元边长。ksqij计算公式：其中θ为ij边对应的三角形单元内角，计算这个系数是为了避免三角形单元被挤压。然后，再解算相应矩阵求解网格各节点的位置。详见文献[3]。删除旧边界映射点及其所在三角形单元，将新边界上的所有离散点视为新节点，按照Delaunay三角化方法插入并维护新边界的完整性。其后，寻找最长边大于给定的边长最大值的所有三角形单元，对这些三角形单元进行分裂。在形心处插点（若没有可分裂的三角形单元，执行第三步）。这样得到一批新节点，一一按Delaunay三角化方法插入。每插入完一批新节点后又得到一批新三角形单元，检验是否可插。直到没有可插的三角形单元为止。用Laplacian光顺法优化网格，优化过程中边界节点位置不变。再检查是否有可分裂的三角形单元，若有重复以上分裂优化过程直到没有为止。

第三步，收缩和优化网格。先搜索可收缩的三角形单元，按前述方法收缩。这时得到的三角形网格并不均匀光顺必须用Laplacian方法优化，优化过程中边界节点位置不变。

4.3 离散方程组的求解和目标函数的计算

离散方程组的求解方法和步骤、进出口条件等的处理已比较成熟，不同的是，在求解过程中，将旧方案计算出的节点物理量值，作为新方案计算的初值。新增加的节点的物理量初值取周围节点的平均值。沿出口边能量积分可算出目标函数值，根据此值，按最优化算法寻优计算。详见文献[4]。