插值法在数值分析中的教学实践
2011-10-25吕晓亚
吕晓亚,张 莉
(内江师范学院 数学与信息科学学院,四川 内江 641112)
数值分析主要研究求解数学模型的算法及有关理论,是求解数学模型的不可缺少的途径和手段,并随着计算机的发展而发展。在信息科学和计算机技术飞速发展的今天,数值分析中的数值方法更显重要。数值分析是一门注重应用的学科,特别注意方法的精确性和计算的效率之间的平衡。传统的教学模式只注重讲授数值方法的原理,算法的理论推导占据了整个教学过程的大部分时间,再加上缺乏实践环节的教学,使得学生不能很好地运用所学的理论去解决实际问题[1]。每种数值方法的讲授都应该尽量地用有一定实际背景的小问题去检验,这样使得学生在掌握数学理论的同时也可以引导学生思考如何应用理论去解决实际的问题,这种教学方法能够激发学生的学习兴趣,使学生对知识的掌握达到理论与实践并举的目的。
数据插值方法是数值分析中的最基本方法之一,主要解决的问题是根据离散数据构造一个简单易于计算的函数代替原有的复杂函数。数据插值的应用非常广泛,例如在建筑工程的外观设计、物理实验中的数据分析与处理、地理信息数据的处理、根据离散数据绘制光滑曲线、图形放大算法等方面[2]。在数据插值方法的教学过程中,通过一个具有实际背景的问题对不同插值方法进行对比分析,不仅有助于学生深刻理解各种插值方法,而且能培养学生的科研能力和创新能力。
1 常用的插值方法
在插值函数中,以多项式函数应用最广。常用的多项式插值有Lagrange插值、Newton插值、Hermite插值及三次样条插值[3]等。
1.1 Lagrange插值法与Newton插值法
设有n+1个互异的插值结点 x0< x1<… < xn,已知对应函数值

则n次Lagrange插值多项式为

其中

Newton插值法是一种利用均差构造插值多项式的方法,n次的Newton插值多项式与n次的Lagrange插值多项式是恒等关系,只是表现的形式不同而已。
1.2 Hermite插值法
Hermite插值法是一种带导数信息的插值方法,常用的有两点三次Hermite插值,即考虑两个插值结点的情形。设两个互异的插值结点 a ≤ x0< x1≤ b ,函数
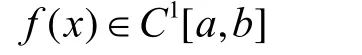
且
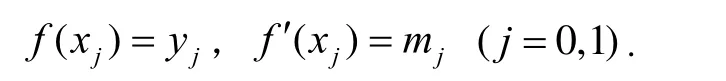
则三次Hermite插值多项式为

上式记为(2),其中

1.3 三次样条插值法
三次样条插值法是一种分段插值法,由于在插值结点处具有二阶导数连续,从而具有更好的光滑性。三次样条插值的思想来源于工程实际问题,而它成熟的数学方法又在工程实际中得到广泛的应用。
给定区间[a,b]上的一个划分:
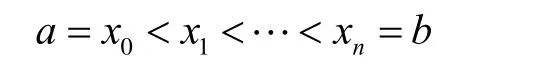
已知函数 f(x)在点xj上的函数值为

如果存在分段函数
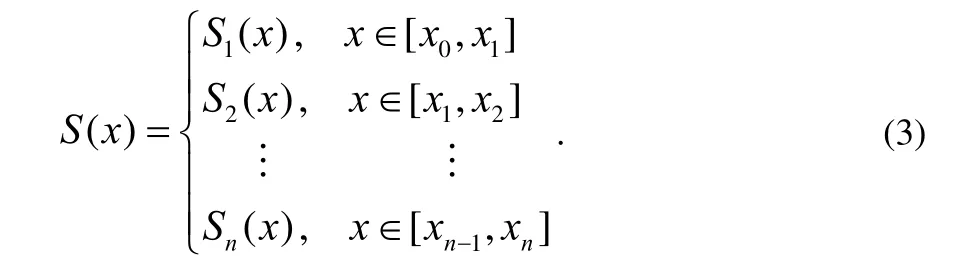
满足条件:
(2)S′′(x)在区间[a,b]上连续;
2 插值法的教学实践
在许多工程建设中,常常会遇到计算断面的面积,如计算土方量及探测矿产储量时,都需要通过断面测量才能实现[4]。下面就以“计算断面面积”为例,对Lagrange插值法、Newton插值法、Hermite插值法及三次样条插值法进行对比分析。如图 1,实测点 P1, P2, … , Pn将地形断面曲线分成n-1段。目前,通常使用的方法是通过插值或逼近来构造出断面的边界曲线,然后再计算断面面积。
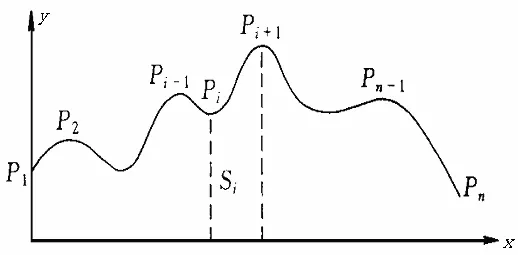
图1 断面曲线
为了作误差分析,采用方程为 y =4 +sin x ,x∈ [0,3π]作为断面的边界曲线,选取的插值信息如表1所示。

表1 插值信息
为了进行对比分析,采用不同类型的三次插值多项式,即三次Lagrange插值多项式(三次Newton插值多项式)、两点三次Hermite插值多项式与三次样条插值多项式来构造边界曲线。其中三次Lagrange插值多项式(三次Newton插值多项式)由于需要4个节点,故有两段曲线,而两点三次Hermite插值多项式与三次样条插值多项式有6段曲线。利用 MATLAB软件绘制出的不同类型三次插值曲线如图 2至图4所示,其中实线部分表示原曲线,虚线部分表示插值曲线。
如果让学生观察图2至图4的结果,将可得到如下结论:两点三次Hermite插值多项式构造边界曲线的效果最好,其次是三次样条插值多项式,效果最差的是三次 Lagrange插值多项式,即两点三次Hermite插值多项式计算断面面积的精度最高,其次是三次样条插值多项式,精度最差的是三次Lagrange插值多项式。

图2 三次Lagrange插值

图3 两点三次Hermite插值
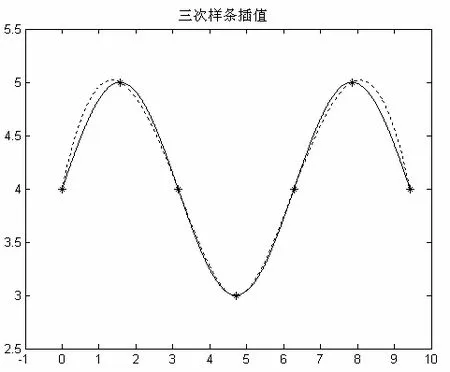
图4 三次样条插值
为了进一步证实结果的正确性,让学生分别计算利用三种插值多项式计算出的断面面积,然后将结果进行对比分析。其对比分析如表2所示。由表2可知,两点三次Hermite插值多项式计算断面面积的误差最小,其次是三次样条插值多项式,误差最大的是三次 Lagrange插值多项式,即所得结论是正确的。

表2 几种计算结果的对比分析
3 结束语
本文主要探讨了数值分析课程中在插值法的教学实践,主要是通过一个具有实际背景的问题对不同插值方法进行对比分析,这样做既可以使学生深刻理解并掌握各种插值方法,又可以开拓学生的视野,培养学生的科研能力和创新能力。当然,数值分析课程中的其它知识点也可以采用这种方式去教学,使学生通过对实际问题的研究,深刻理解知识点,达到理论与实际相结合的效果。
