AR-GARCH模型在股票市场的应用
2011-10-21辛海明
辛海明
(中山大学 新华学院,广东 广州 510520)
AR-GARCH模型在股票市场的应用
辛海明
(中山大学 新华学院,广东 广州 510520)
本文介绍了AR-GARCH模型,以及当前国内外的研究情况,并利用此模型对从2003年1月7日到2010年11月19日的上证指数进行实证分析.结果表明,在股票价格序列中普遍存在的尖峰厚尾现象在上证指数中同样存在,还有明显的异方差性,并且AR-GARCH模型可以很好的拟合股指收益率波动情况.
AR-GARCH模型;广义自回归条件异方差;收益率
随着市场经济的不断发展和受国外投资策略的影响,越来越多的人都意识到了投资理财的重要性,希望通过合理的投资使自己获得高于银行利率的收益,因此收益与风险历来都是投资者和学者们关注的热点问题.对未来收益大小的度量与预测则是每个投资者在投资决策前必须考虑的基本问题.一般地说,股票市场价格呈现显著的波动性,这种波动性随时间变化,股票投资充满了风险,因此对股票收益率进行拟合是有意义的.1982年Engle在分析英国通货膨胀序列时,发现经典的ARIMA模型始终无法取得理想的拟合效果,最后经过对残差序列的研究,发现问题出在残差序列具有异方差性.而股票收益率有明显的异方差性,因此用GARCH模型拟合股票收益率是比较好的.
1 GARCH模型
1.1 ARCH模型
ARCH模型的全称是自回归条件异方差模型(autoregressive conditional heteroskedastic),它的完整结构如下:

式(1)中,Var(εt)=ht,f(t,xt-1,xt-2,…)为{xt}的 Auto-Regressive模型模型的实质是使用误差平方序列的q阶移动平均拟合当期异方差函数值.由于移动平均模型具有自相关系数q阶截尾性,所以ARCH模型实际上只适用于异方差函数短期自相关过程.
1.2 GARCH模型
在实践中,有些残差序列的异方差函数是具有长期自相关性的,这时如果使用ARCH模型拟合异方差函数,将会产生很高的移动平均阶数,这会增加参数估计的难度并最终影响ARCH模型的精度.为了修正这个问题,,Bollerslov在1985年提出了广义自回归条件异方差(generalized autoregressive conditional heteroskedastic,GARCH)模型,它的结构如下:

式(2)中,Var(εt)=ht,f(t,xt-1,xt-2,…)为{xt}的回归函数(0,1).这个模型简记为GAR(p,q).GARCH模型是至今为止最常用、最可行的异方差序列拟合模型.但它的有效使用必须满足如下两个约束条件.
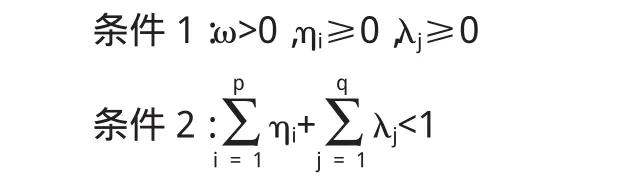
1.3 AR-GARCH模型
对残差序列{εt}拟合GARCH模型有一个基本要求:{εt}为零均值、纯随机异方差序列.有时回归函数f(t,xt-1,xt-2,…)不能充分提取原序列{εt}中的相关信息,残差序列可能具有自相关信息,残差序列可能具有自相关性,而不是纯随机的.这时需要对{εt}先拟合自回归模型,再考察自回归残差序列{vt}的方差性,如果{vt}异方差,对它拟合GARCH模型.这样构造的模型称为AR(m)-GAR(p,q)模型:

式(3)中,Var(vt)=ht,f(t,xt-1,xt-2,…)为{xt}的回归函数(0,1).
除了上述介绍的ARCH、GARCH、AR-GARCH模型外,还有其他形式的GARCH模型,如:EGARCH、IGARCH模型等.因为本文仅采用AR-GARCH模型,故不在此作介绍.
2 沪市AR-GARCH模型的实证分析
2.1 数据选取
本文所收集的数据为从2003年1月7日到2010年11月19日的上证指数的收盘价格,共计1907个.设日收益率为rt,clpr为收盘价格,则最近一日的收益率为rt=(log(clpr)-log(lag(clpr))),其中lag(clpr)为前一日的收盘价格.
2.2 收益率序列的白噪声和平稳性检验

图1 收益率的时间序列图

图2 收益率的白噪声和平稳性检验
对收益率序列进行白噪声和单位根检验可知(如图2),收益率序列是平稳非白噪声序列.
2.3 收益率序列的正态性检验
从图3收益率的描述性统计结果可以看出,上证指数的收益率具有以下一些统计特征:样本数据偏度小于0,而峰度大于3,表明我国证券市场股票收益率存在尖峰厚尾性,所以不服从正态分布.

图3 收益率的描述性统计结果
另外,从图4的正态性检验也可以看出,各种正态检验的p值小于0.01,即显著拒绝原假设.

图4 收益率的正态性检验结果
2.4 收益率序列异方差检验

图5 收益率的异方差检验结果
从图5中可以看出,直到高阶收益率序列仍然存在着强烈的异方差性,因此用GARCH模型来拟合数据是合理的.
2.5 AR-GARCH模型模拟及拟合效果检验
经过收益率序列异方差检验结果可知,用AR-GARCH模型拟合是合理的,经过模拟,则在显著性水平为0.05下,得到的模型为AR(2)-GARCH(1,1):

由图6可知,模型的各个参数除了收益率一阶回归常数显著为零外,其余参数都显著不为零,并且η1+λ1=0.9929<1,符合GARCH模型要求.Durbinh为0.226接近0.05.

图6 AR-GARCH模型参数拟合结果及检验
3 结论
选择谨慎科学的收益率度量模型,对我国目前处于发展初期不发达的股票市场来说尤其重要.本文中的AR(2)-GARCH(1,1)模型能较好地描述我国沪市收益率的“易变性聚类”现象,能对未来的收益率进行很好地预测.从而可在大部分区间内反映收益分部的“厚尾”特性将这一模型与风险价值VAR方法相结合,还可以进行较准确的风险度量.
〔1〕朱世武.基于SAS系统的金融计算[M].清华大学出版社,2005.
〔2〕王燕.应用时间序列分析(第二版)[M].中国人民大学出版社,2009.
〔3〕李克娥,陈圣滔.基于GARCH模型的上证指数的Var分析[D].长江大学数学与信息学院学位论文,2008.
〔4〕吴霖.基于GARCH模型的股票市场价格波动分析[J].价值工程,2010(50).
F83
A
1673-260X(2011)02-0099-02
