基于序列线性规划方法的型钢混凝土梁的优化
2011-10-20朱杰江陈庭军
朱杰江, 陈庭军
(上海大学 土木工程系,上海 200072)
基于序列线性规划方法的型钢混凝土梁的优化
朱杰江, 陈庭军
(上海大学 土木工程系,上海 200072)
在改进的带步长限制的序列线性规划 (sequential linear programming,SLP)优化思路基础上,编制优化程序,并将其应用到型钢混凝土和钢筋混凝土梁的优化中.实例表明,该优化方法收敛快速且准确.通过对型钢混凝土和钢筋混凝土优化结果的比较可知,钢筋混凝土梁在无梁高限制时较型钢混凝土梁经济.
序列线性规划;型钢混凝土梁;钢筋混凝土梁;优化;二次插值
1 优化模型
1.1 基本变量
取型钢混凝土梁典型截面为优化模型,如图 1所示.图中,b为截面宽度,h为截面高度,As为受拉钢筋面积,A′s为受压钢筋面积,Asv为箍筋截面积,s为箍筋间距,bf为型钢翼缘宽度,tf为型钢翼缘厚度,hw为型钢腹板高度,tw为型钢腹板厚度,c为受拉钢筋保护层厚度,as为受拉钢筋合力点至混凝土受拉边距离 (考虑到配筋量较大,采用双排钢筋,取60 mm),a′s为受压钢筋合力点至混凝土受压边距离,a为型钢受拉翼缘和受拉钢筋共同作用合力点至混凝土受拉边距离,h0为型钢受拉翼缘和受拉钢筋共同作用合力点至混凝土受压边距离,a′a为型钢受压翼缘合力点至混凝土受压边的距离,δ1h0为型钢腹板上端至截面上边缘距离,δ2h0为型钢腹板下端至截面上边缘距离.

图 1 型钢混凝土梁典型截面Fig.1 Typ ical section of steel reinforced concrete composite beam
考虑受压钢筋、腰筋按构造配置,型钢腹板沿梁高充满布置,只在两端留置构造要求的间距,故受压钢筋、腰筋和型钢高度均不作为优化变量.型钢混凝土梁的优化变量为 b,h,As,Asv,s,bf,tf,tw.
1.2 目标函数
本研究中的单位长度造价考虑了混凝土、型钢、纵筋、箍筋和模板的造价,并且各材料单价均按照现行定额标准和人材机单价及考虑材料、加工等各种费用的综合单价,较符合工程实际.取目标函数为

式中,fObj为梁单位长度总造价,Cc为混凝土综合单价,Aa为型钢截面积,Ca,Cs,Csv分别为型钢综合单价、纵筋综合单价、箍筋综合单价,Cf为模板综合单价,ρ为钢材密度,取 7.85 t/m3,其余符号意义同前.
1.3 约束条件
参考《型钢混凝土组合结构技术规程》(JGJ138—2001)[6]的要求,列出以下约束条件.

(1)抗弯要求如下:式中,M为弯矩设计值,x为混凝土受压区高度,Maw为型钢腹板承受的轴向合力对型钢受拉翼缘和受拉钢筋合力点的力矩 (计算详见文献[6]),Naw为型钢腹板承受的轴向合力(计算详见文献[6]),Aaf,分别为型钢受拉、受压翼缘面积,为界限相对受压区高度,fc为混凝土受压强度设计值,为型钢受压强度设计值,α1,β1为系数.这里未考虑受压钢筋的作用.
(2)抗剪要求如下:

式中,V为剪力设计值,fyv为箍筋抗拉强度设计值,fa为型钢受拉强度设计值,ft为混凝土抗拉强度设计值 ,βc为系数.
(3)构造要求如下:
型钢含量要求为
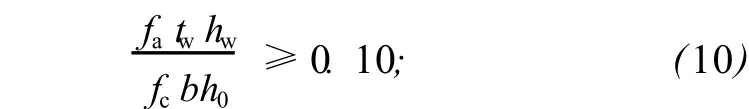
最小配筋率要求为

高宽比要求为
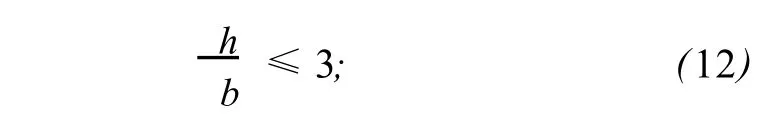
翼缘宽度要求为
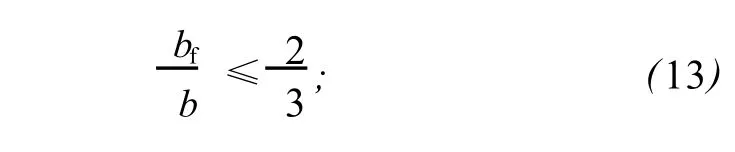
翼缘宽厚比要求为

腹板高厚比要求为

(4)正常使用极限状态要求如下:
最大裂缝宽度要求为

最大挠度要求为

式中,ωmax,ωlim分别为最大裂缝宽度和裂缝宽度限值,f,flim分别为梁最大挠度和挠度限值 (详见文献[6]).
1.4 优化模型
将优化模型综合,即求


同时 ,xil≤xi≤xiu,i=1,2,…,8,xil,xiu分别为变量的下限和上限.
2 SL P方法简介
2.1 SL P方法基本原理
对带约束的非线性优化问题,有
min Z=f(X),
s.t. gj(X)≤0, j=1,2,…,m,
X =[x1,x2,…,xn]T.
将目标函数、约束条件按泰勒级数展开,取一次项,得到线性表达式为
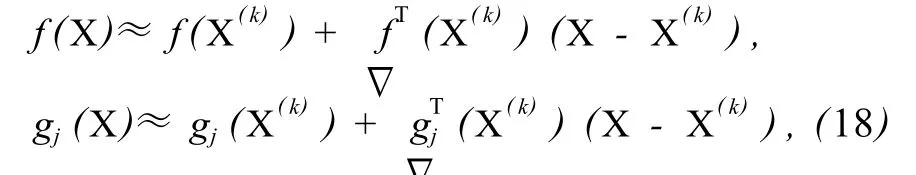
式中,X(k)为第 k次循环后得到的变量.
此时,原问题转化为线性规划问题,可以采用单纯形法寻找最优解,并将得到的最优解取代 X(k)进行下一循环,直至满足精度要求.由于单纯形法一般能准确稳定地得到最优解,故 SLP方法具有快速、准确的优点.
2.2 改进的带活动限制的 SL P方法
实践经验表明,单纯使用 SLP方法有时会出现最优解附近存在振荡的问题,因此,可采用活动限制法 (move limitmethod)来克服上述缺点[7].该方法即在原有 SLP方法的基础上附加如下约束条件:

Bhavikatti[8]在带活动限制的 SLP方法的基础上作了以下几点改进,使其在工程应用中更加有效.
2.2.1 将变量“拉回”可行域
当设计变量位于不可行区域时,采用下述方法将设计变量“拉回”至可行域约束边界附近以继续优化:
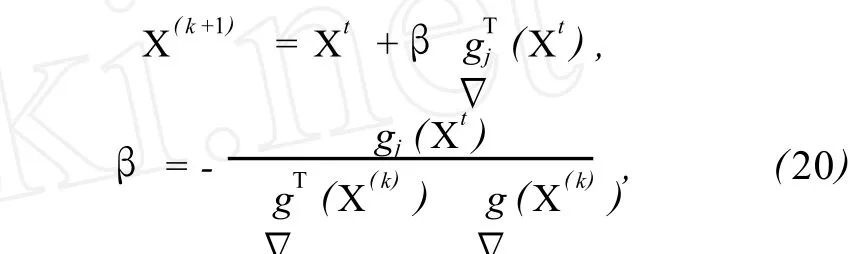
式中,X(k+1)为“拉回”后的设计变量,Xt为位于不可行区域的设计变量,Xk为上一个循环得到的设计变量,gj(Xt)为超出可行域边界最大的约束.该步骤的几何意义如图 2所示.

图 2 将点“拉回”可行域并判断方向可行性Fig.2 Steer the point into feasible area and the judgement of the usability of d irection
若一次未能将设计变量“拉回”至可行域,可以多次尝试该步骤;若仍不能“拉回”至可行域,可以重新计算 Δg(Xt),再继续上述步骤;若经过一定次数尝试均未能将设计点“拉回”至可行域,可以直接进行下一循环,即允许中间循环中出现不可行点,以保证程序的连续运行及最后稳定收敛.
若变量超出了上 (下)限,可以将该变量赋值为上 (下)限,再检查约束对该变量的一次偏微分的符号,如有超出上 (下)限的趋势,则将该偏微分定义为零.
2.2.2 二次插值
当采用单纯形法得到一个新的变量值时,若此时的目标函数值比上一循环目标函数值大,则采用二次插值法 (quadratic interpolation technique)寻找更优解,即当 f(X(k+1))>f(X(k))时,得

式中,
α*f(X(k)),f(X(k+1))分别为第 k,k+1次循环的目标函数值,X*为二次插值后的设计变量,M,M(k)分别为修正后和原来的活动限制向量,即进行了二次插值,同时将活动限制缩小同样的比例.若M小于精度要求,则结束优化,待重新设定初值后,再进行新的优化.二次插值的几何意义如图 3所示.

图 3 二次插值Fig.3 Quadratic interpolation
2.2.3 方向可行性的检验
上述二次插值须在方向可行的前提下执行,即

2.3 程序框图
根据上述理论,我们自行编制了优化程序,主要步骤如下:
(1)选定一初始点,检验该点是否在可行域内,若不在,则将其“拉回”至可行域内;
(2)定义此时变量为旧变量,目标函数值为旧值,判断循环次数是否超过了限值,如果是,转至步骤(9);
(3)将目标函数、约束条件进行泰勒级数展开,得到线性规划模型,然后求解单纯形;
(4)检验得到的新解是否在可行域内,若不在,则将其“拉回”至可行域;
(5)将新的目标函数值与旧值比较,若二者差值满足精度要求,可认为已收敛至最优解,转至步骤(8),否则,进行下一步;
(6)若新值小于旧值,即目标函数减小,则转至步骤 (2),否则,进行下一步;
(7)若此时方向可行,则进行二次插值,找到使目标函数值比旧值小的新点,若插值后的新点落在可行域外,则将其“拉回”至可行域,转至步骤 (2),若方向不可行,直接转至步骤 (2);
(8)将此时的点定义为最优解,优化结束;
(9)在限制循环次数下,无法收敛,优化结束.
根据上述步骤,程序框图如图 4所示.

图 4 SL P方法的程序框图Fig.4 Flow d iagram of SL Pmethod
3 优化实例
本工作为体现型钢混凝土的优越性,采用大跨度、大荷载简支梁,并改变梁高上限,与钢筋混凝土进行比较.一简支型钢混凝土梁参数如下:跨度 l0=10.0 m,楼板传来恒载 g1k=35.8 kN/m,楼板传来活载 qk=20.0 kN/m,型钢混凝土梁自重g2k=[As+Aa+Asv(b+h-100)/s]×78.5×10-6+(bh-Aa-As)×24.5×10-6kN/m.
采用 C 30混凝土、HRB 335纵筋、HPB 235箍筋、Q345型钢 ,c=25 mm,Cc=364.323元 /m3,Cs=Csv=Ca=5 534.775元 /t,Cf=39.298元 /m2.300≤b≤600,600≤h≤1 200,402≤As≤8 000,57≤Asv≤308,50≤s≤300,50≤bf≤500,6≤tf≤40,6≤tw≤20.优化结果如表1所示.
钢筋混凝土梁优化模型从略,约束条件参考《混凝土结构设计规范》(GB50010—2002)[9].考虑抗弯、抗剪、裂缝、挠度及构造要求等约束,改变梁高上限,比较型钢混凝土和钢筋混凝土优化效果,结果如表2所示.

表1 型钢混凝土梁优化结果Table 1 Optim ized results of steel reinforced concrete composite beam

表2 不同梁高上限时型钢混凝土和钢筋混凝土优化结果的比较Table 2 Com par ison of RC beam and steel reinforced concrete composite beam w ith d ifferent section height upper lim its
由表1可以看出,型钢混凝土梁的优化效果显著,而其中型钢尺寸趋于下限,可见型钢“性价比”较钢筋低.由表2可以看出,随着梁高上限的下降,型钢混凝土与钢筋混凝土造价差逐渐减小,直至低于钢筋混凝土.可见在没有梁高限制时,钢筋混凝土梁较型钢混凝土梁经济;在一定梁高上限约束下,型钢混凝土较钢筋混凝土经济.本工作算例初值尺寸未取自现有工程,但能代表现有工程的一般设计取值,可以反映现有工程中型钢混凝土设计存在造价偏高的情况.
图 5为本例型钢混凝土梁优化的迭代过程.整个优化过程不到 10步便收敛,可见该方法收敛快速且稳定,目标函数在开始时下降很快.

图 5 SL P方法优化收敛过程Fig.5 Optim izated convergence process of SL Pmethod
4 结 论
由经过改进的带步长限制的 SLP方法在型钢混凝土和钢筋混凝土梁优化中的应用,得到以下结论.
(1)型钢混凝土中钢筋较型钢更经济,即优化使型钢尺寸趋于下限,而通过加大钢筋用量满足约束.
(2)型钢混凝土梁优化在荷载较大时,有效约束为挠度、裂缝、宽高比等,而抗弯、抗剪约束均有富余,箍筋一般按构造配置.故在优化中,可以不考虑抗剪约束、箍筋面积和箍筋间距等变量.
(3)在大跨度、大荷载下,若梁高没有限制,采用钢筋混凝土较型钢混凝土经济;但梁高限制到一定程度时,钢筋混凝土必须依靠加大梁宽来满足约束,此时型钢混凝土较钢筋混凝土经济.
(4)本工作改进的 SLP方法优化程序收敛快速且稳定,具有一定的工程意义.
本工作将改进的 SLP方法应用在型钢混凝土梁的优化中,取得了较理想的效果和有价值的结论,但仍然存在一些局限尚待继续改进.
(1)假设变量为连续型,但实际工程中通常为离散变量,如何将 SLP程序应用到离散变量的优化中.
(2)未考虑到钢筋的配置等构造要求,得到的优化解可能在实际应用中需要进一步调整.
(3)如何将该优化思路应用到结构整体优化中(如框架等),并考虑更多的变量和约束条件,如钢筋等级、混凝土等级和型钢截面形式等.
[1] 范良宜.钢筋混凝土矩形截面梁实用优化设计方法[J].基建优化,1998,19(3):27-29.
[2] 张靖静.钢筋混凝土受弯构件正截面设计优化分析[J].工业建筑,2005,35(2):100-102.
[3] 刘海军,吴子燕,艾兵,等.钢筋混凝土梁的优化设计[J].基建优化,1997,18(3):29-32.
[4] 斯剑华.钢筋混凝土受弯构件优化分析[J].河南科学,2004,22(3):374-376.
[5] 刑国雷,张陵,刘志方.基于遗传算法的钢筋混凝土梁离散优化设计[J].基建优化,2003,24(6):44-46.
[6] 中国建研院.中华人民共和国行业标准 (建工版)JGJ138—2001型钢混凝土组合结构技术规程 [S].北京:中国建筑工业出版社,2001.
[7] 张炳华,侯昶.土建结构优化设计 [M].2版.上海:同济大学出版社,1988:150-159.
[8] BHAV IKATTI S S. Structural optimization using sequential linear programming[M].New Delhi:V IKAS Publishing House PVTLtd,2003.
[9] 中华人民共和国建设部.中华人民共和国国家标准GB50010—2002混凝土结构设计规范 [S].北京:中国建筑工业出版社,2002.
Optim ization of Steel Reinforced Concrete Composite Beam Based on Sequential L inear Programm ing M ethod
ZHU Jie-jiang, CHEN Ting-jun
(Department of Civil Engineering,ShanghaiUniversity,Shanghai200072,China)
Based on the improved move limit method of the theory of sequential linear programming(SLP),thispaper develop a program applied to optimization of steel reinforced concrete composite and reinforced concrete beams.Practical examp les indicate that the op timization method converges quickly and accurately.Besides,reinforced concrete beam is more economical than steel reinforced concrete composite beam without constraint on the height of beam section according to the comparison of their optimized results.
sequential linear p rogramming(SLP);steel reinforced concrete composite beam;reinforced concrete beam;optimization;quadratic interpolation
TU 375
A
1007-2861(2011)02-0203-06
10.3969/j.issn.1007-2861.2011.02.017
2009-08-21
朱杰江 (1963~),男,教授,博士后,研究方向为结构优化及结构抗震.E-mail:zhujjt@126.com
(编辑:孟庆勋)
目前,对钢筋混凝土梁的优化方法有优化准则法、网格搜索法、复合形法、库-塔克最优条件、遗传算法等[1-5].很多优化过程只取部分主要变量,且由于搜索最优解的盲目性,得到的可能不是最优解,且迭代次数也较多.本研究采用序列线性规划(sequential linear programming,SLP)方法 ,在变量多、搜索方向明确的条件下,可以在较少的迭代次数情况下收敛到最优解.单纯配置钢筋的混凝土梁由于截面尺寸及配筋率的限制,承载能力有限.若采用型钢混凝土梁,则可以大大提高承载能力,且没有配筋率的限制,并可以在大跨度结构中使用.型钢混凝土梁的延性好,有利于抗震设计.由于型钢混凝土梁的优化较少涉及,因此,本研究应用 SLP方法对型钢混凝土梁的优化进行有益的探索.
