T形线散射电流的麦克斯韦电路
2011-10-20吴明亮沈文辉薛昌韡梅冠香
吴明亮, 沈文辉, 薛昌韡, 梅冠香
(上海大学通信与信息工程学院,上海 200072)
T形线散射电流的麦克斯韦电路
吴明亮, 沈文辉, 薛昌韡, 梅冠香
(上海大学通信与信息工程学院,上海 200072)
运用最新提出的麦克斯韦电路理论,分析 T形线的散射电流.将该结构等效为 LC电路,求解与之对应的微分方程,得到该结构的散射电流.数值实验分别计算了 T形线的等效电路参数 L,C,α,β,以及相应的散射电流.分析结果表明,所得电路参数和散射电流符合物理现象,并且与矩量法的结果以及相关文献中的结果均吻合,从而证明了该方法的正确性和有效性.
麦克斯韦电路;T形线;散射电流;矩量法
本研究将麦克斯韦电路理论应用于分析 T形线的散射问题,通过将 T形线等效成 LC电路,结合交点和端点的边界条件,构建出微分方程.通过求解该方程,可以确定该结构的散射电流.数值实验分别计算了 T形线的等效电路参数 L,C,α,β以及相应的散射电流,所得结果符合物理现象.计算所得散射电流与矩量法的结果以及相关文献中的结果均吻合,从而表明了本研究提出方法的正确性和有效性.
1 理论分析
1.1 结构分析
T形线及尺寸如图 1所示.以原点为交点,可将该结构看成三段直导线的并联,三段导线的半径都为 a,各段直导线的长度分别为 L1,L2,L3,其上电流分别为 I1,I2,I3.显然,交点处满足如下条件[12-13]:①标量位 V连续,即 V1(0)=V2(0)=V3(0);②电流满足 I1(0)-I2(0)+I3(0)=0.
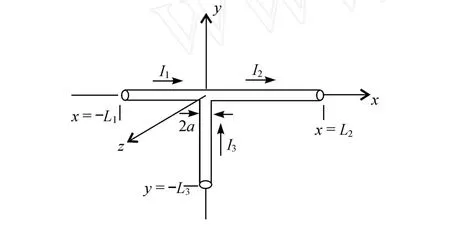
图 1 T形线示意图Fig.1 Schematic d iagram of T-shaped w ires
将该 T形线等效成 LC电路,该电路对应的微分方程为[4]

式中,L,C分别为单位长度的等效电感和等效电容,αV,βI为由于结构的不连续性而引起的能量泄漏,α,β为电压相关源系数和电流相关源系数,为入射电场的切向分量.如果等效电路参数 L,C,α,β确定,则方程 (1)将唯一确定.
1.2 等效电路参数提取
式 (1)中,L,C,α,β4个未知数可由 2组电流和电压决定,而电流可以通过边界条件确定.根据麦克斯韦电路理论的唯一性定理[3],边界条件的设定不影响系数 L,C,α,β的取值,因此,设 2组边界条件如下:

然后,由矩量法结合边界条件式 (2)可以求得相应的表面电流.再根据洛伦兹条件,确定出相应的线上电压.最后,将所求得的 2组电压和电流代入式(1),可得等效电路参数 L,C,α,β.一旦等效电路参数确定,则 T形线对应的微分方程式 (1)就唯一确定了.
在用矩量法求解 T形线表面电流的过程中,需要用到如下无激励源的海伦方程[12]:
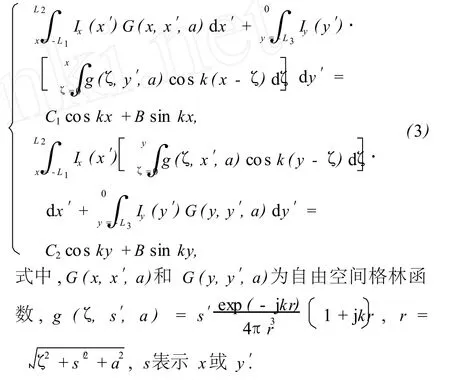
将 T形线分成N等份,未知电流用分段脉冲函数展开,采用点选配法,则式 (3)可以离散化为矩阵形式.求解该矩阵可以很方便地得到 T形线的表面电流.
1.3 微分方程求电流
经过上述分析可以确定该结构对应的微分方程,接着由该微分方程求 T形线的散射电流.首先,将该结构分成 N等份,式 (1)离散为[3]

终端边界条件为
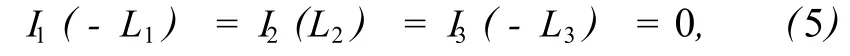
式 (4)~(5)中,d=L/N为每小段导线的长度,In,Vn,Einc
n分别为第 n小段上的散射电流、线上电压和入射场场强.结合终端边界条件式 (5)以及连接点处的条件 (1)和 (2),可求得 T形线各段直导线上的散射电流.
式 (4)的矩阵形式为一个高度稀疏矩阵,占用的内存空间很小(O(6N)).而矩量法的阻抗矩阵是一个满矩阵,占用内存空间很大 (O(N2)).因此,采用麦克斯韦电路理论的微分方程求解问题可占用较少的计算机资源.
2 计算实例
为了验证上述分析的正确性,本研究对如下 2种 T形线进行了数值计算.
2.1 对称结构 T形线
该结构与文献[14]中对应的模型结构相同,相应的导线长度为 L1=L2=0.11λ,L3=0.33λ,导线半径为 a=0.002 22λ.图 2所示为该结构对应的等效电路参数 L,C,α,β曲线.图中可见,等效电路参数在导线 L1和导线 L2上呈对称、反对称性,在各段的端点和交点处呈跳跃状.
图3所示为在入射场E—inc=y^e-jkz照射下T形线产生的散射电流.图中表明本方法不仅与矩量法计算结果吻合,同时也与文献 [14]中的计算结果吻合,从而证明了本方法的正确性.图 4所示为在入射场E—inc=x^e-jkz照射下T形线产生的散射电流,有趣的是在这种情况下 I3=0.原因是由于该 T形线呈对称结构,导线 L1和导线 L2在导线 L3上的耦合作用相互抵消.因此,I3=0符合物理现象,这从另一面证明了本方法的正确性.

图 2 对称 T形线结构的 L,C,α,β曲线Fig.2 Curves L,C,α,β of symmetr ical T-shaped w ires

图 3 T形线散射电流分布,入射场 E—inc=y^e-jkzFig.3 Scatter ing currents of T-shaped w ires,the incident f ield is E—inc=y^e-jkz
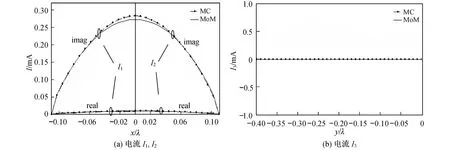
图 4 T形线散射电流分布,入射场 E—inc=x^e-jkzFig.4 Scatter ing currents of T-shaped w ires,the incident field is E—inc=x^e-jkz
2.2 非对称结构 T形线
该结构相应的导线长度为 L1=0.2λ,L2=0.3λ,L3=0.4λ,半径为 a=0.002 5λ.图 5所示为该结构对应的等效电路参数曲线.图中可见,L,C,α,β在各段导线终端和交点不连续处呈跳跃状.图 6所示为在入射场 E—inc=x^e-jkz照射下 T形线产生的散射电流.图 7所示为在入射场 E—inc=y^e-jkz照射下 T形线产生的散射电流.由图可见,本方法的计算结果与矩量法的结果一致.
另外,采用本方法计算对称结构 T形线的时间为 15.782 s,相应的矩量法的计算时间为15.703 s;计算非对称结构 T形线的时间为 27.484 s,相应的矩量法的计算时间为 26.016 s.可见,两种方法的计算时间相当.麦克斯韦电路理论所得微分方程各参数具有电路特性,为电磁场辐射和散射问题的研究提供了一种新的途径.而矩量法已经相当成熟,求解精度高,一般作为衡量其他方法的标准.

图 5 非对称 T形线结构的 L,C,α,β曲线Fig.5 Curves L,C,α,β of unsymmetr ical T-shaped w ires

图 6 T形线散射电流分布,入射场 E—inc=x^e-jkzFig.6 Scatter ing currents of T-shaped w ires,the incident field is E—inc=x^e-jkz

图 7 T形线散射电流分布,入射场 E—inc=y^e-jkzFig.7 Scatter ing currents of T-shaped w ires,the incident f ield is E—inc=y^e-jkz
3 结 束 语
本研究利用麦克斯韦电路理论分析了 T形线的散射电流.通过将该结构等效成 LC电路,结合交点和各段导线的终端条件,求解微分方程得到相应的散射电流.该微分方程生成的矩阵是一个高度稀疏矩阵,占用的内存空间很小 (O(6N));而矩量法的阻抗矩阵是一个满矩阵,占用的内存空间很大(O(N2)).数值实验分别计算了对称 /非对称 T形线的等效电路参数 L,C,α,β及相应的散射电流.结果表明,交点处和终端处的参数 L,C,α,β呈明显跳跃状,其他部分都呈现连续性,这体现了等效电路参数与几何形状有关的性质.显然这种关系符合物理现象.同时,本研究计算结果不仅与矩量法的计算结果一致,而且与相关文献中的结果一致,证明了本方法的正确性和有效性.值得指出的是,本方法不仅适用于 T形线,同样也可以推广到任意直导线相交结构的散射电流计算中.
[1] 哈林顿.计算电磁场的矩量法[M].北京:国防工业出版社,1981:6-18.
[2] YEE K S.Numerical solution of initial boundary value p roblems involving Maxwell’s equations in isotrop ic media [J]. IEEE Transactions on Antennas and Propagation,1966,14(3):302-307.
[3] MEI K K.Theory of Maxwellian circuits[J].Radio Sci Bull,2003,305:6-13.
[4] L IL,L IU Y W,MEI K K,et al.Applications of the Maxwellian circuits to linear wire antennas and scatterers[J]. IEEE Transactions on Antennas Propagation,2006,54(10):2725-2730.
[5] KHOUSA M A,ZOUGHI R.Maxwellian circuits-based analysis of loaded wire antennas and scatterers[J].IEEEAntennas and Wireless Propagation Letters,2008,7:318-320.
[6] HEM,XU X W.Maxwellian circuitmodels for analysis of printed spiral antennas[J]. IEEE Trans M icrow Wireless Compon Lett,2005,15(11):769-771.
[7] WU M L,SHEN W H,ZHAO G H,et al.Comprehensive analysis of linear wire antennas with Maxwellian circuits[C]∥Proceedings of 2008 China-Japan Joint M icrowave Conference.Shanghai:Shanghai University Press,2008:327-329.
[8] SHEN W H,WU M L,MEIK K.Application of MEIto Maxwellian circuits[C]∥2009 IEEE International Symposium on Antennas and Propagation.Charleston:The Institute of Electrical and Electronics Engineers Press,2009:1-4.
[9] HONG J S,L IU Y W,WANG B Z,et al.A novel differential equation model for amicrostrip low-pass filter[J].M icrowave and Op tical Technology Letters,2002,35(5):368-370.
[10] L IU YW,HONG J S,MEI K K.Analysis of a double microstrip discontinuity using generalized transmission line equations[J].IEEE Trans Adv Packag,2003,26(4):368-374.
[11] LEUNG K W,L IU Y W,YANG P,et al.Maxwellian circuits and Green’s functions[J].M icrowave and Optical Technology Letters,2004,41(4):318-320.
[12] BUTLER C M.Currents induced on a pair of skew crossed wires[J].IEEE Transactions on Antennas and Propagation,1972,20(6):731-736.
[13] TAYLOR C D.Electromagnetic scattering from arbitrary configurations of wires[J]. IEEE Transactions on Antennas and Propagation,1969,17:662-663.
[14] CHAO H H,STRA IT B J.Radiation and scattering by configurations of bent wires with junctions[J]. IEEE Transactions on Antennas and Propagation,1971,19:701-702.
上海大学期刊社接受市新闻出版行业文明单位评选考核验收
2011年 3月 11日,上海市新闻出版局报刊处陈丽处长一行,代表市新闻出版局对上海大学期刊社进行新闻出版行业文明单位评选考核验收.
此次文明单位评选活动在上海市新闻出版行业尚属首次,目的在于以此为抓手,推动各新闻出版单位提升综合实力、实现全面发展.考核验收是评选活动中的一个重要环节,包括听取汇报、座谈交流、现场巡视和问卷调查等几个步骤.
汇报暨座谈交流会于上午 10时在我校出版大楼二楼会议室召开,出版社党委书记、社长郭纯生主持会议,校党委宣传部副部长刘绍学致欢迎辞,期刊社社长秦钠以《创美德讲原则文明在心,务进取求卓越文明在行——上海大学期刊社创建文明单位工作汇报》为主题作专题汇报.回顾了近年来期刊社精神文明创建工作的制度、组织、措施、活动及成果,以及创建工作在期刊社实现全面发展和重点突破过程中的重要作用.
在随后的座谈交流中,陈丽处长充分肯定了上海大学期刊社近年来在提高办刊质量、提升刊物的社会影响力等方面取得的显著成绩,并就此次新闻出版行业文明单位评选活动的举办目的、运作方式等作了简要说明.《应用科学学报》执行主编王朔中教授和《社会》执行主编仇立平教授作为校办期刊主编代表先后发言,感谢新闻出版局、上海大学及期刊社为期刊发展提供的广阔空间和大力支持,感谢编辑部同仁所付出的辛勤劳动.与会人员还就期刊年检、学术期刊改制、数字化出版等问题进行了深入交流.
会后,陈丽处长一行对期刊社办公场所进行了现场巡视和指导,期刊社 20位编辑接受了市新闻出版行业精神文明建设问卷调查,并就新闻出版行业的精神文明建设积极建言献策.
Scatter ing Current Analysis of T-Shaped W ires w ith the Theory of M axwellian Circuits
WU Ming-liang, SHEN Wen-hui, XUE Chang-wei, Kenneth K.Mei
(School of Communication and Information Engineering,ShanghaiUniversity,Shanghai200072,China)
The scattering current of T-shaped wires is analyzed with the recently proposed theory of Maxwellian circuits(MC).The structure is equivalent to LC circuit,and the scattering currents can be worked out from the differential equations relevant to the circuit. In the numerical experiments,circuit parameters L,C,α,β and scattering currents of two T-shaped structures are calculated.The analysis shows that circuit parameters and scattering currents are not only in accordance with the physical concepts,but also agreewith the resultsof the method of moments(MoM),and with those reported in the literature.Thus the described method is valid and efficient.
Maxwellian circuits;T-shaped wires;scattering currents;method of moment(MoM)
TN 823;O 241.8
A
1007-2861(2011)02-0132-06
10.3969/j.issn.1007-2861.2011.02.005
2009-10-20
上海市重点学科建设资助项目 (S30108);上海市科委重点实验室开放课题资助项目(SKLSFO201005)
沈文辉 (1972~),男,讲师,博士,研究方向为计算电磁学、遗传算法和微带天线等.E-mail:haomeni@163.com
(编辑:赵 宇 )
(上海大学期刊社)
随着计算机技术的蓬勃发展,计算电磁学也得到了长足发展,出现了多种数值计算方法,如矩量法[1]、时域有限差分方法 (finite difference time domain,FDTD)[2]等.通常,这些传统数值方法都是从场的角度分析电磁场问题.最新提出的麦克斯韦电路 (Maxwellian circuits,MC)理论[3]从电路角度出发,将场问题等效成 LC电路,通过求解该电路对应的微分方程得到场问题的解.人们对该理论进行了深入研究,已经将其应用到部分线天线[4-8]和部分微带传输线[9-11]中.对于散射问题,目前已将该理论应用到了直线散射体[4]及加载直线散射体上[5],并取得了满意的结果.
