基于DV-hop的无线传感器网络定位算法研究*

张 震，闫连山，刘江涛，李晓银

(西南交通大学信息科学与技术学院信息光子与通信研究中心，成都 610031)

无线传感网络(Wireless Sensor Network，WSN)由大量无线传感器节点组成，现已广泛应用在军事、环境、医疗等领域［1－2］。节点定位技术是无线传感网络得以广泛应用的前提条件，网络中的传感器节点发回监测区域内的温度、压力、湿度等数据信息只有与位置信息相关联才有意义［3－4］。节点的定位技术是无线传感网络获取信息的关键技术，正逐步受到了越来越多的关注［5］。

现有的无线传感器节点定位技术可以分为两类:基于测距的定位技术［6］和无需测距的定位技术［7－8］。基于测距的定位技术需要测量节点间的距离或角度信息，测量精度高;无需测距的定位技术不需要直接测量节点间的距离或角度信息，对节点的硬件要求低。出于对传感器网络成本、功耗等因数的考虑，以及在大多数应用场合下对节点的定位精度要求不高，所以现阶段对无需测距的定位技术研究较多。

DV-hop算法是目前研究和应用最为广泛的无需测距定位算法，但在计算未知节点和锚节点间的距离时估算较粗糙。现阶段，对DV-hop算法的改进方法主要有:(1)与其他的定位算法相结合［9］;(2)修正未知节点与锚节点间的距离［10］;(3)改进最后一步的定位计算方法［11］等，而对DV-hop算法本身的参数优化研究较少。本文对DV-hop算法中的参数进行了详细的分析，并通过仿真对参数进行优化。仿真结果表明，通过参数优化可以有效地提高DV-hop算法的定位精度。

1 DV-hop算法介绍

DV-hop［12－13］算法主要通过距离矢量和跳数来估测未知节点到锚节点的距离，然后使用三边或多边测量法求出未知节点的位置信息。在未知节点的通信范围内，锚节点数目并不多，采用上述方法可以得到节点到其通信范围外的多个锚节点的距离信息。DV-hop算法主要由以下三步组成:

第1阶段:通过典型的距离矢量路由协议，使网络中所有的节点获得到锚节点最小跳数值。

第2阶段:锚节点计算平均每跳距离值，如果一个锚节点的坐标为(xi，yi)，则平均每跳距离计算公式为:

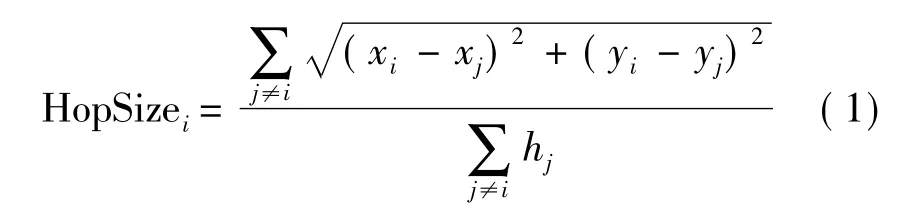
式中(xj，yj)表示锚节点j的坐标;hj表示锚节点j到锚节点i的最小跳数;HopSizei表示锚节点i计算的平均每跳距离。将HopSizei作为一个校正值，在传感器网络中采用可控泛洪法进行广播，传感器节点只保存第一个校正值，以此保证节点接收到的校正值是最近的一个锚节点发送过来的，未知节点收到校正值后就可以根据跳数和校正值计算其到锚节点的距离。

第3阶段:当未知节点至少获得到三个锚节点的距离时，通过使用最小二乘法计算未知节点的坐标。给定一个锚节点集Ri=(xi，yi)T，i=1，2，…M，M表示锚节点的数目，并且未知节点X=(x，y)T到锚节点i的最小跳数是Li，因此未知节点X=(x，y)T到锚节点i的距离值为di=Li×HopSizei，未知节点X的坐标可以通过下列公式计算得:

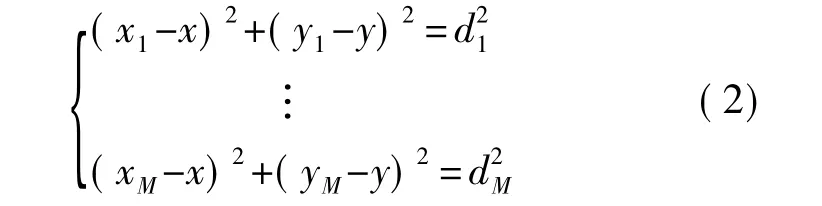
将前面的(M－1)个方程依次减去最后一个方程得到:

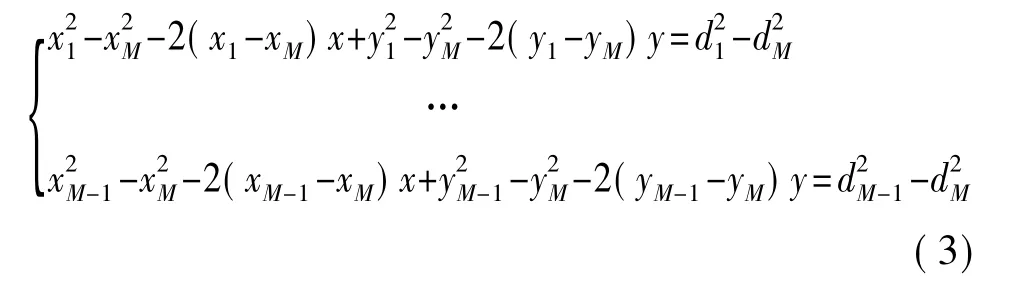
式(3)的线性方程表示方式为

其中

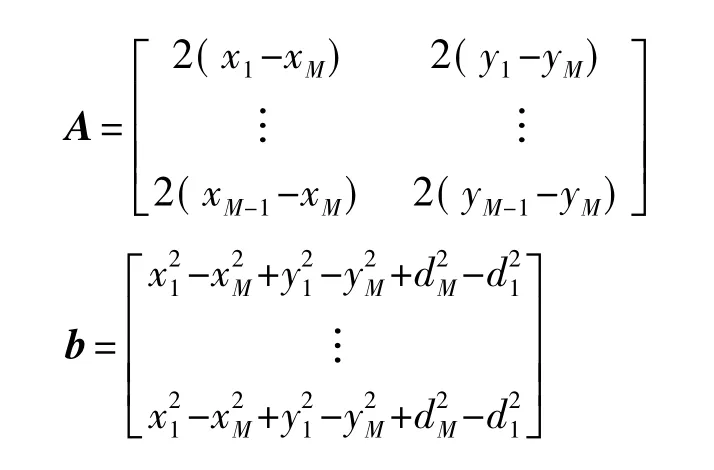
使用标准的最小均方差估计方法可以得到未知节点X的坐标为:

DV-hop算法定位误差［14］主要来源于用曲线距离代表直线距离。平均每跳距离的估计很粗糙，并且多方面影响距离的估测，如锚节点数目、节点的通信半径、总节点数目等。

2 DV-hop算法参数分析

2.1 锚节点数目

在DV-hop定位算法中，未知节点的位置是根据估算的未知节点到锚节点的距离，并利用三边定位法，计算出未知节点的坐标。由于锚节点和未知节点都是随机分布的，如果锚节点分布在一条直线上或近似在一条直线上，或者锚节点相距很近，那么式(2)中的某些方程就可以约去，导致最后参与未知节点位置估计的锚节点只有几个甚至式(5)不成立，又由于估测出来的未知节点到锚节点的距离di本身就有一定的误差，因此锚节点的数目及分布情况对节点的定位精度有很大的影响。

2.2 节点通信半径

DV-hop算法是通过跳数和平均每跳距离来估测未知节点到锚节点的距离，而跳数和节点的通信半径有关系，节点通信半径不同会使两个节点之间的跳数不同，如图1所示。

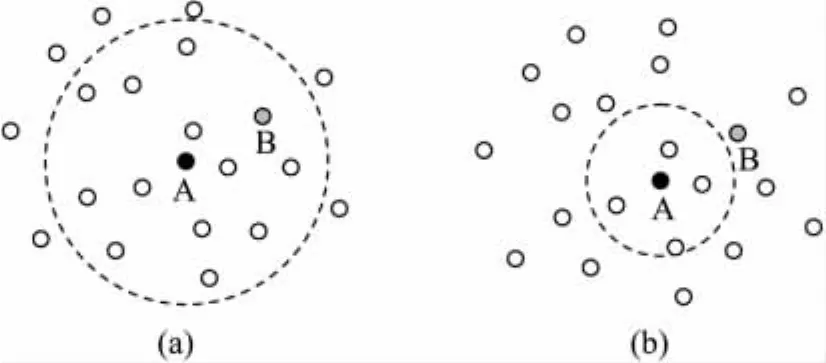
图1 不同的节点通信半径和跳数的关系

在图1中，由于节点的通信半径不同，在图1(a)中节点A与节点B之间的跳数是1跳，而在图1(b)中，节点A与节点B之间的跳数是2跳。在不同的节点通信半径下，估测出来的两节点之间的距离就相差很大，从而影响节点的定位精度，因此节点的通信半径不同会导致不同的定位精度。

2.3 总节点数目

在一定面积的传感区域内，不同的传感器节点总数同样影响DV-hop算法的定位精度。如图2所示，在相同的节点通信半径下，节点总数不同，平均一跳内的节点数目会相差很大。如果节点数目过少，可能会出现在锚节点的通信范围内没有节点，其它节点接收不到锚节点的信息，导致节点无法定位的情况。

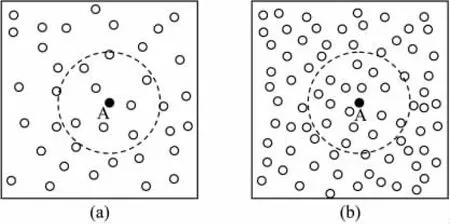
图2 不同的节点数目

3 仿真结果及分析

由上述分析可知，DV-hop算法中锚节点的个数、节点的通信半径、节点的总个数均会对节点的定位误差产生影响。本小节具体给出了在100 m×100 m的无线传感器网络区域内，当锚节点个数、节点的通信半径、总节点个数变化时的节点定位误差的仿真结果，并对其做了分析。

在无线传感器网络中锚节点个数不同，节点的定位精度不同，仿真结果如图3所示。在图3(a)中，传感器节点总数为100个，取节点通信半径R分别为15、25、50，对应锚节点的个数B从3～30变化时。在图3(b)中，节点通信半径为25，取传感器节点总数分别从100、300、500，对应锚节点的个数B从3～30变化。

图3 锚节点个数不同时节点的定位精度

从图3(a)和(b)中可以看出:当节点的通信半径和节点总数分别不同时，锚节点的个数B=12左右，节点的定位误差能降低到较小值;当锚节点的个数从3～10变化时，节点的定位误差迅速减少;随着锚节点个数继续增加，节点的定位误差虽有所减小，但幅度趋于平缓。由以上分析可知，当锚节点的个数达到一定数量时，其对节点定位误差的影响降低，且锚节点本身成本较高，说明节点通信半径和节点总数不同时，在锚节点个数为12处，节点定位误差基本接近最小值。

为了研究节点的通信半径R不同时，节点定位误差的变化情况，本文给出了在总节点数为100，锚节点个数分别为6、8、10、12时，节点通信半径R从10～50变化，节点的定位误差变化情况，结果如图4所示。

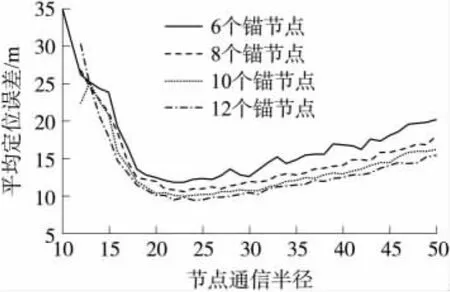
图4 在不同的节点通信半径下定位误差值

在图4中，给出了不同锚节点个数下，节点通信半径R从10～50变化时节点的定位误差。从图4可以看出:随着锚节点个数的逐渐增加(6～12变化时)，节点的定位误差相应的降低;在不同锚节点个数下，当节点通信半径从10～20变化时，节点定位误差迅速减少，并达到最小值，随着节点通信半径的继续增加，节点的定位误差也开始增加，说明当锚节点不同时，总节点数100时，存在最优R值。

为了使仿真的结果更加真实有效，图3和图4中的数值均是100次仿真结果求得的平均值。综合考虑图3和图4可以得出:在100 m×100 m的区域内，总节点数目为100的条件下，当锚节点的个数B=12，节点的通信半径R=22 m时，节点的定位误差较小。在本文的后续仿真中，在100 m×100 m的无线传感器网络区域内，取锚节点的个数为12。

为了研究无线传感器网络区域内总节点个数不同时，最优节点通信半径是否变化，以及最低节点定位误差的变化情况，图5分别给出了总节点数在100、300、500处，节点通信半径R从5～50变化时，节点定位误差的变化情况。

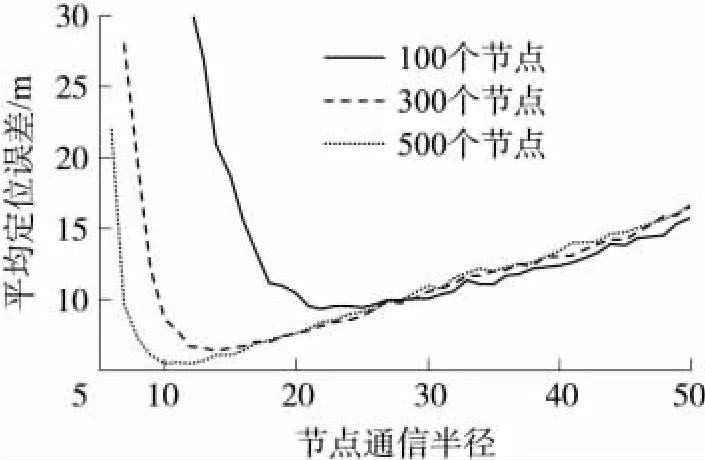
图5 在不同的节点通信半径下定位误差值

从图5中可以看出，随着总节点数的增加，节点的定位误差整体都在下降，并且最优的节点通信半径也在变化，表1给出了在不同总节点数下，对应的最优节点通信半径和相应的最低节点定位误差值。

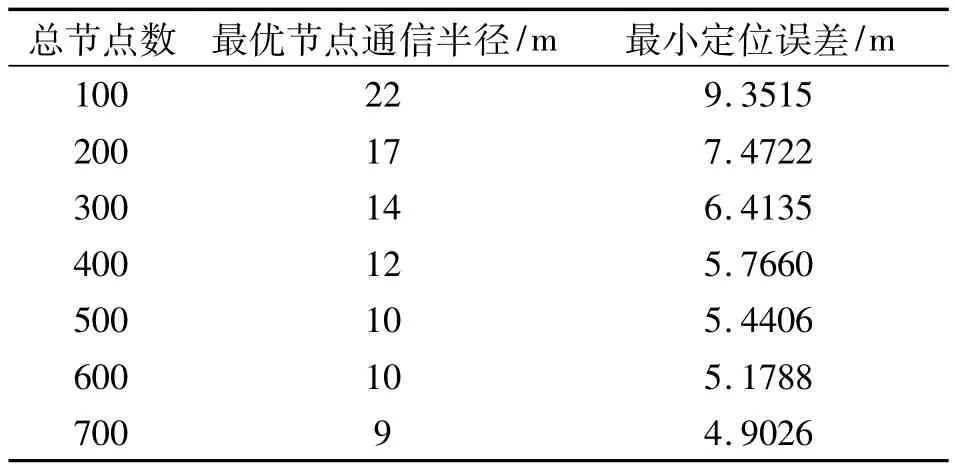
表1 不同总节点数下的最优节点通信半径和定位误差

综合图5和表1可得:在不同的总节点数目条件下，存在最优的节点通信半径，使定位误差降低到最低值。要想使DV-hop算法的定位精度达到最好，可以根据表1，在不同总节点数目下，选择最优的节点通信半径，从而使节点的定位误差降低到最小值。

4 结论

本文主要对基于DV-hop算法的无线传感器网络自身定位进行了研究，首先详细介绍了DV-hop算法的步骤。然后分析了影响DV-hop算法的定位精度的主要参数包括:锚节点个数、节点的通信半径、网络中的总节点数。经分析和仿真结果表明:在100 m×100 m监测区域内，锚点节点个数为12左右，并且针对不同总节点数，选择合适的节点通信半径，可以使节点的定位误差降低到较低值。

［1］Ren F Y，Huang H N，Lin C.Wireless Sensor Network［J］.Journal of Software，2003，4(7):1282－1291.

［2］Akyildiz L F，Su W，Sankarasubramaniam Y，et al.A Survey on Sensor Networks［J］.IEEE Communications Magazine，2002，40(8):102－114.

［3］李晓维，徐勇军，任丰原.无线传感器网络技术［M］.北京:北京工业大学出版社，2007，1－17.

［4］戴莹，王建平，张崇巍.无线传感器网络节点定位算法的研究也改进［J］.传感技术学报，2010，23(4):567－570.

［5］王福豹，史龙，任丰原.无线传感器网络中的自身定位系统和协议［J］.软件学报，2005，16(5):857－868.

［6］Xiao J，Ren L R，Tan J D.Research of TDOA Based Self-Localization Approach in Wireless Sensor Network［J］.Intelli-Gent Robots and Systems，2006，(10):2035－2040.

［7］Li M，Liu Y H.Rendered Path:Range-Free Localization in Anisotropic Sensor Networks with Holes［J］.IEEE/ACM Transactions on Networking，2010，18(1):320－332.

［8］赵清华，刘少飞，张朝霞，等.一种无需测距节点定位算法的分析和改进［J］.传感技术学报，2010，23(1):122－127.

［9］胡斌，李方敏，刘新华.基于RSSI量化模型的定位算法研究［J］.武汉理工大学学报，2009，31(23):92－95.

［10］刘少飞，赵清华，王华奎.基于平均跳距估计和位置修正的DV-Hop定位算法［J］.传感技术学报，2009，22(8):1154－1158.

［11］王书锋，侯义斌，黄樟钦，等.无线感知网络最小二乘法定位算法的误差分析与优化［J］.系统仿真学报，2009，21(19):6211－6215.

［12］Niculescu D，Nath B.DV Based Positioning in ad hoc Networks［J］.Journal of Telecommunication Systems，2003:22(1－4):267－280.

［13］Niculescu D，Nath B.Ad hoc Positioning System(APS)Using AOA［C］//INFOCOM 2003.22nd Annual Joint Conference of the IEEE Computer and Communications.San Francisco，USA，2003.IEEE Societies(3)，1734－1743.

［14］He T，Huang C，Blum B M，et al.Range-Free Localization Schemes for Large Scale Sensor Networks［C］//Proceedings of the 9th Annual International Conference on Mobile Computing and Networking，San Diego，2003.ACM Press，81－95.