任意层导电板上方线圈阻抗的级数计算模型*

张思全，胡盛斌，陆文华

(上海工程技术大学航空运输学院，上海 201620)

在石油、化工、航空等领域，许多关键设备和部件由多层导电材料制成，对其内部缺陷和结构完整性的检测是一个较困难的问题。超声检测法虽具有可检测较厚材料的优势，但不适于检测相邻层间含有空气的多层导电结构。电涡流检测技术利用材料中缺陷与涡电流、线圈激励电磁场之间相互作用引起线圈阻抗变化的原理来检测缺陷并对结构完整性进行评价，并且具有不需耦合剂、可检测多层导电结构隐藏缺陷的优势［1－4］。

如何快速、精确求解线圈阻抗是涡流检测的重要问题。数十年来，许多学者对此进行了研究。Dodd和Deeds研究了正弦电流激励线圈位于有均匀厚度导电材料覆层的半无限大导电平板上方的情况，得到了积分形式的矢量磁位闭合解析解［5］;其后，Luquire等人又研究了线圈置于任意层导电结构中间时的阻抗变化模型［6］。在国内，雷银照研究了半无限大导体上方覆盖一定厚度金属涂层构成的两层平板导电结构的轴对称涡流解析解［7］;黄平捷研究了置于多层导电结构上方线圈响应与多层导电结构厚度变化之间的关系模型［8］;范孟豹推导了位于任意层导电结构上方涡流探头的阻抗解析模型，在阻抗计算中引入符号运算法求解矢量磁位表达式系数，减小了程序计算量［9］。但这些研究采用径向无限大导体，所得解为积分形式，存在计算困难、时间花费大的问题。

本文在前人研究基础上，采用解域截取法分析矩形截面圆柱线圈置于任意层导电平板上方的正向问题，推导涡流检测探头线圈与任意层导电结构相互作用的级数形式阻抗变化计算模型。为验证模型的正确性，针对单层导电结构的特例，计算了线圈置于其上方时的阻抗变化，分析了影响计算精度的主要因素，并与有限元计算结果进行了对比。

1 任意层导电板上方线圈阻抗计算

1.1 任意层导电板上方单匝线圈阻抗计算

1.1.1 任意层导电板上方单匝线圈的矢量磁位

如图1a)所示，一个单匝通电圆形线圈置于任意层(设为n层)导电平板上方，其轴线与任意层平板表面垂直;设各层平板的厚度、电导率、介电常数都是任意的，各层介质都是线性、各向同性、均匀的。设线圈中为正弦激励电流。采用圆柱坐标系O－(r，φ，z)，各单位矢量分别为er，eφ，ez。设线圈轴与Z轴重合，与任意导电平板表面的交点为原点O，线圈的半径为r0，线圈在平板上方的提离距离为z0。任意层导电结构最下方第1层，记为L1，设其相对磁导率为μr1，电导率为σ1，在实际运算中可假设其厚度为无限大或为0。自下往上，各层结构编号、电磁参数与厚度表达式依次增加，即第i层记为Li，相对磁导率为μri，电导率为σi。最上方第n层导电平板记为Ln。通电圆环线圈下方空气层(0＜z＜z0)记为Ln+1，线圈上方(z＞z0)空气层记为Ln+2。

图1 线圈位于径向被圆柱边界截取的多层导电结构上方

许多文献在研究多层导电结构时，研究区域为无穷大，电磁场以傅立叶－贝塞尔积分项的形式表示，在数值计算时收敛很慢。将积分变为级数形式，并通过调整级数的求和项数来控制计算的精度和速度可达到提高计算速度的目的。为此，在距离线圈适当距离处施加一个圆柱形边界并令边界处的解为零，就得到一个被截取的圆柱形解域，这样虽然会增加解的误差，但只要包含足够多项，用级数解代替积分解就不会影响计算精度［10－11］。

1.1.2 矢量磁位的边值问题

麦克斯韦方程组是涡流检测的理论基础。为了简化电磁场的计算及分析，引入矢量磁位A。

图1中所有区域被与线圈同轴、半径为b的圆柱面截取，从下至上，共有n+2个区域，有n+1个相邻层之间界面zk，其中k=1，2，…，n，n+1。zk也表示各界面的z轴坐标。

半径为r0的单线圈位于内边界面z=z0平面内，其电流密度可以用δ函数写为

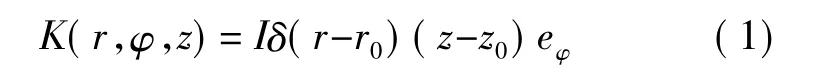
式(1)中I为单匝线圈激励电流的幅值。由于介质和场源关于对称轴r=0呈轴对称分布，所以图1中场的矢量磁位仅含有周向分量Aφ。

忽略位移电流，在一个各向同性、线性均匀媒质中，单匝线圈在(r0，z0)处产生的矢量磁位A(r，z)满足下列约束方程及其边界条件［5］:

(1)约束方程

式(2)中i=1，2，3，…，n+2，表示相应的层数;=－jωμriμ0σi;当I≠0 时，各区域矢量磁位非零且有界。

(2)边界条件

在所有界面zi，i=1，2，…，n，n+1，满足:

在界面zi，i=1，2，…，n，满足:

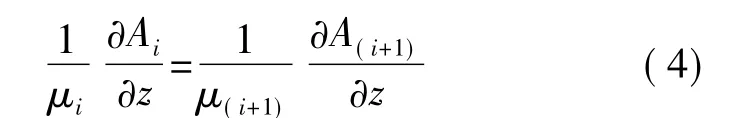
圆形单线圈的上下区域，即第Ln+1区域和Ln+2区域之间界面zn+1满足:

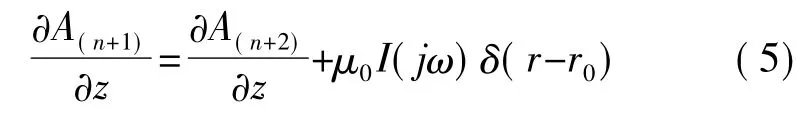
1.1.3 矢量磁位约束方程的通解

在圆柱坐标系下，约束方程式(2)可写为:

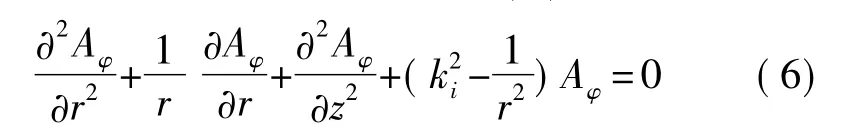
用分离变量法求解式(6)得:

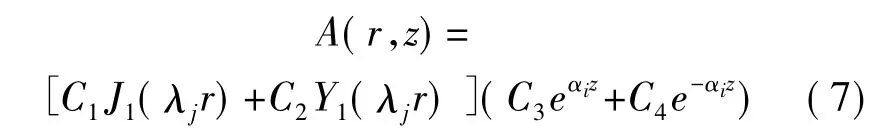
式(7)中J1(λjr)和Y1()分别是第一类和第二类一阶贝塞尔函数。λj称为分离常数，它与r和z无关，由于在r=b处施加了截取边界，所以引入离散本征值λj来代替Dodd和Deeds模型中的连续值，由J1(λjb)=0可求得本征值λj。式(7)中

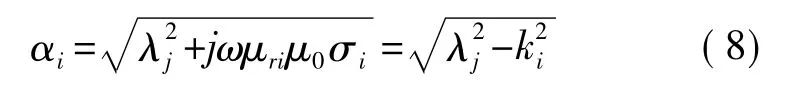
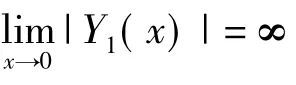
第L1层

第Li层，i=2，…，n+1

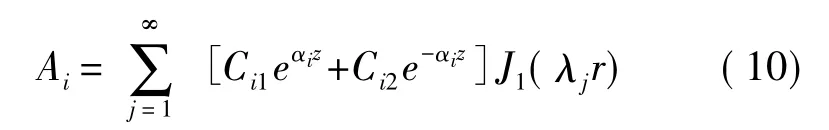
第Ln+2层

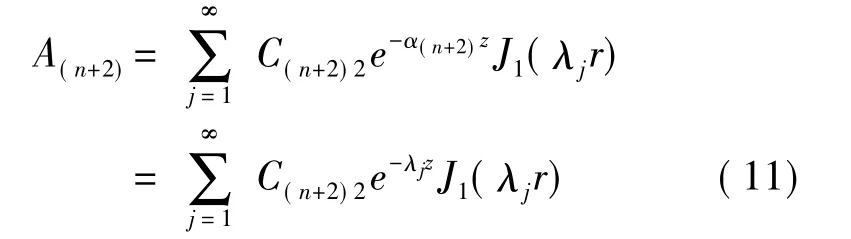
根据边界条件式(3)，在界面z=zi，i=1，2，…，n，n+1，满足

根据边界条件式(4)，在界面z=zi，i=1，2，…，n，满足

根据式(5)、式(10)和式(11)，并利用贝塞尔函数的正交性

线圈上下区域交界面z=zn+1=z0，满足

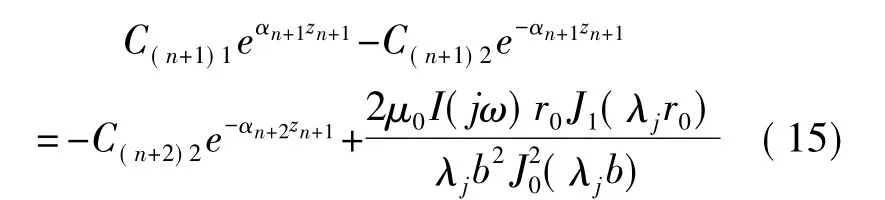
这样，共得到2n+2个方程，需要求解2n+2个未知系数。

1.1.4 矢量磁位的求解

在导电结构层数较多时，各层矢量磁位的系数较复杂，将式(13)重写为

式(16)中定义

利用式(12)、式(16)，对界面z=zi，i=1，2，…，n，因为C12=0，可以求解得到以下关系

在界面z=zn+1，因为C(n+2)1=0，并且第Ln+1、Ln+2层为空气，αn+1=αn+2=λj，由式(12)可得

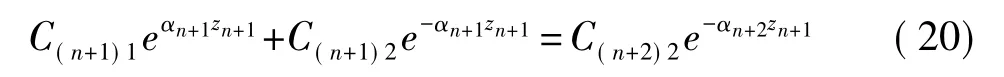
由式(15)、式(20)可得

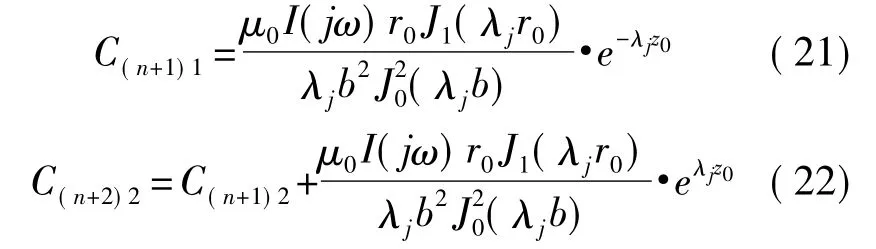
式(18)、式(19)可写成矩阵形式

令Ti为式(23)中的转换矩阵，则各系数之间关系可写为

令

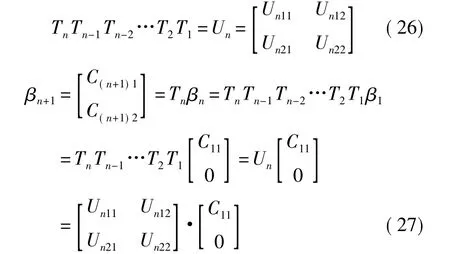
因此

将式(21)代入式(29)得

由式(22)、式(30)可得

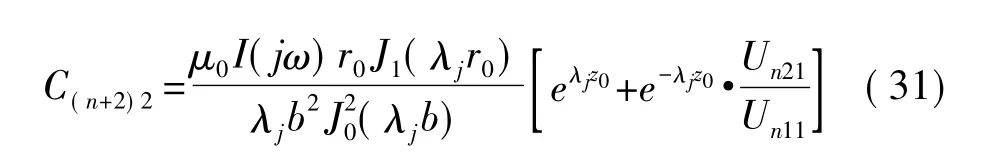
由式(21)、式(28)得

这样可以得到任意区域矢量磁位的系数，进而可以写出任意区域的矢量磁位。其中解析计算中要利用线圈上、下方区域的矢量磁位。

线圈上方区域的矢量磁位

线圈下方区域的矢量磁位

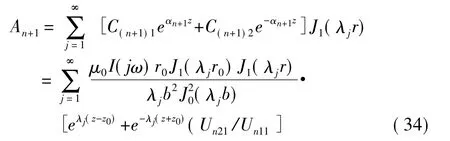
1.2 任意层导电平板上方多匝线圈阻抗计算

确定了由单匝线圈在Li(i=1，2，…，n+1，n+2)区域的矢量磁位Ai(r，z)后，对于图1b)所示具有矩形截面的多匝线圈，可以通过将单匝线圈导出的矢量磁位沿线圈横截面积分获得各区域总的矢量磁位:

在获得矩形截面多匝线圈上方Ln+2区域总的矢量磁位和下方Ln+1区域总的矢量磁位后，令中的l2为z，令中的l1为z，并将两式相加，可以得到线圈区域任一点的矢量磁位Atotal。利用公式V(r，z)=jω2πrAtotal(r，z)可以获得单线圈上的感应电动势，通过叠加可以得到m匝线圈的自感电压为

从而得出任意层导电结构上方m匝线圈阻抗为:

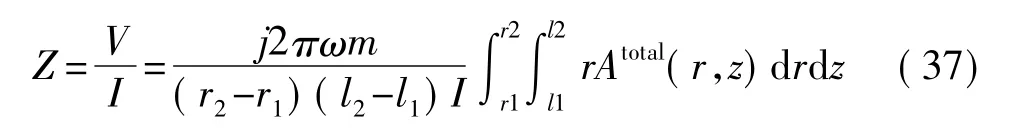
式(37)中，I为单匝线圈内的电流幅值。

2 单层导电结构上方线圈阻抗计算

为了验证所导出任意层导电结构上方m匝线圈阻抗表达式(37)的正确性，下面计算单层导电结构上方线圈阻抗的特例。

2.1 单层导电结构上方单匝线圈的矢量磁位

则置于单层导电结构上方线圈的阻抗变化为

令式(23)中的转换矩阵Ti中的i取1，可得单层导电结构中转换矩阵T1;令式(33)、式(34)中的n=1，可分别得到单层导电结构线圈上部区域L3和下方区域L2的矢量磁位A3、A2

图2 多线圈位于单层导电结构上方

2.2 单层导电结构上方多匝线圈的阻抗计算

确定了单匝线圈上下区域的矢量磁位A3、A2后，对于图2所示具有矩形截面的圆柱线圈，可以利用式(35)通过将单匝线圈的矢量磁位沿线圈横截面积分获得总的矢量磁位。

计算中采用线圈电流密度

可分别得到m匝线圈上方区域矢量磁位和m匝线圈下方区域矢量磁位。令中的l2=z中的l1=z，并将两式相加，可得m匝线圈区域的矢量磁位A(2－3)为

利用式(36)，通过叠加可以得到探头线圈的自感电压为

从而得出单层导电结构上方圆柱形线圈的阻抗表达式为:

式(42)中

m为矩形线圈的匝数，I为单匝线圈内的电流幅值。m匝线圈的电流密度如式(39)所示。

式(38)中的单层导体上方线圈阻抗Zw即为式(42)。令Zw中α1=λj、μr1=1即得到无导体时的线圈阻抗Zh

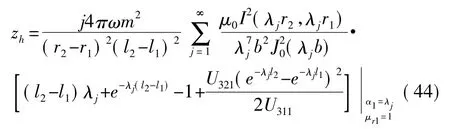
利用式(38)即可计算出单层导电结构中涡电流引起的线圈阻抗变化为

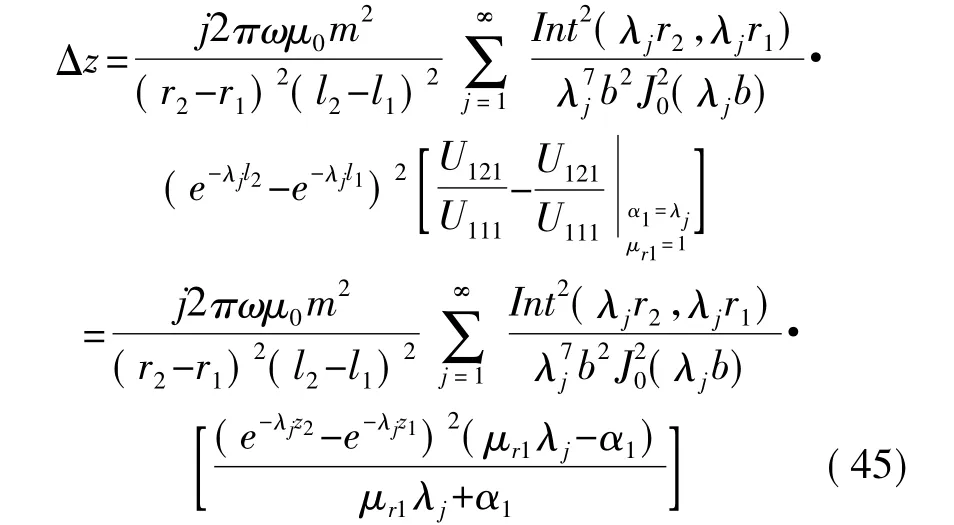
2.3 级数展开计算及有限元仿真验证

为了检验级数计算法的正确性，采用Mathematica软件，根据式(45)，在不同线圈激励频率下，对线圈阻抗变化情况进行了计算。计算中所采用线圈及导电结构参数如表1所示。

表1 线圈及导电结构相关参数

为验证级数计算法的正确性，同时采用有限元法对置于单层导电板上方线圈的阻抗变化进行仿真计算。一般文献通常采用ANSYS软件［12］，这里采用Maxwell 2D电磁场计算软件进行仿真。首先构造如图3所示的2D模型，由于模型关于线圈轴对称，所以只需画出一半;然后指定模型的材料属性，并设定边界条件和激励源;在模型左边界施加奇对称边界条件，在线圈上施加电流激励源;设定求解参数，将线圈上的阻抗与电感值包含在计算过程中。

如图3所示进行网格划分，并设定求解器残差，最后启动求解过程。

图3 2D有限元模型及网格划分

在不同激励频率下，将级数展开法与有限元仿真计算所得的阻抗变化结果进行了对比，其中电阻和电抗的对比分别如图4、图5所示。在级数法计算中，取解域截取半径b=30r2，计算级数前150项的和。

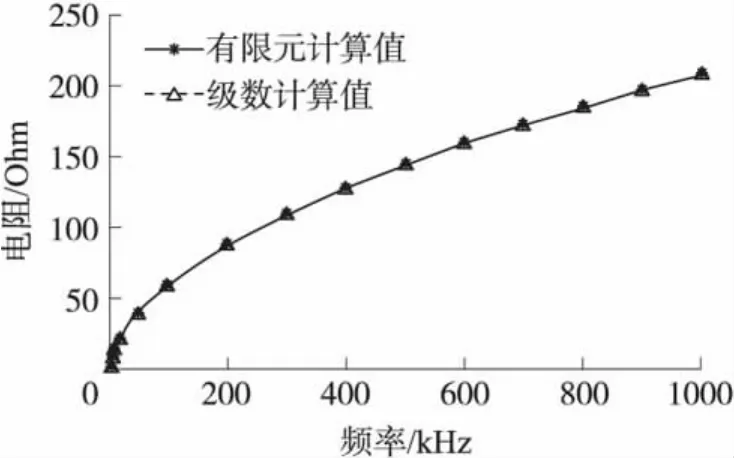
图4 线圈电阻变化与激励频率关系

图5 线圈电抗变化与激励频率关系

由图4、图5可见，级数法计算所得线圈阻抗变化值与有限元仿真计算结果能够很好吻合，验证了级数展开计算模型的正确性。

3 讨论

为进一步研究解域截取半径与求和项数的不同选择对级数法计算线圈阻抗变化值精度的影响，在激励频率为1 kHz、10 kHz、50 kHz和100 kHz下，分别取解域截取半径b=10r2和b=30r2，分别计算级数前50项和前150项的和，计算中所采用线圈及导电结构参数如表1所示。计算各参数下级数法与仿真计算法所得线圈阻抗变化值之间的相对误差，结果如表2所示。

表2 级数计算与有限元仿真结果之间的相对误差单位:%

由表2中可见，在较大的截取半径b=30r2情况下，如果级数相加项数为较少的30项，则所得计算结果误差大于较小截取半径b=10r2的情况;但如果将级数求和项数增大到150项时，计算精度就大于b=10r2的情况。这说明一个较大的截取半径需要更多的求和项来保证较好的计算精度。

级数计算式(42)、式(45)中只有截取半径b和求和项数需要确定，积分项Int(x1，x2)仅依赖于线圈内外半径r1和r2，而与线圈的提离和材料特性无关，可以提前计算。因此级数计算法可获得较快的计算速度。

4 结论

从Maxwell方程组出发，引入矢量磁位，采用解域截取和变量分离的涡流检测线圈阻抗计算方法，将有限层导电平板推广到任意层，导出了位于任意层有限区域导电平板上方线圈阻抗变化的模型，用易于计算的级数解代替积分解，拓宽了经典线圈阻抗计算公式的应用范围，提高了计算速度，这在需要计算大量阻抗值的情况下非常有用。对单层导电结构的特例进行了计算并用有限元仿真方法进行了验证，证明了级数展开计算方法的正确性，可以应用在多层导电结构缺陷涡流检测法定量检测正向模型中。

［1］Theodoulidis T，Poulakis N，Dragogias A.Rapid Computation of Eddy Current Signals from Narrow Cracks［J］.NDT＆E International，2010，43:13－9.

［2］Guohou Li，Pingjie Huang，Peihua Chen，et al.Quantitative Nondestructive Estimation of Deep Defects in Conductive Structures［J］.International Journal of Applied Electromagnetics and Mechanics，2010，33(3－4):1273－1278.

［3］Sun Y S，Ouyang T，Udpa S.Remote Field Eddy Current Testing:One of the Potential Solution for Detecting Deeply Embedded Discontinuities in Thick and Multilayer Metallic Structures［J］.Materials Evaluation，2001，59(5):632－637.

［4］张玉华，孙慧贤，罗飞路，等.一种用于盘孔裂纹检测的差动式涡流探头的设计与实现［J］.传感技术学报，2008，21(6):1079－1083.

［5］Dodd C V，Deeds W E.Analytical Solutions to Eddy Current Probe-Coil Problems［J］.Journal of applied physics，1968，39(6):2829－2838.

［6］Luquire J W，Deeds W E，Dodd C V.Alternating Current Distribution Between Planar Conductors［J］.Journal of Applied Physics，1970，41(10):3983－3991.

［7］雷银照，马信山.涡流线圈的阻抗计算［J］.电工技术学报，1996，11(1):17－20.

［8］黄平捷，吴昭同，郑建才，等.多层厚度电涡流检测反演算法及实验研究［J］.仪器仪表学报，2005，26(4):428－432.

［9］范孟豹，黄平捷，叶波，等.多层导电结构厚度电涡流检测解析模型及实验验证［J］.中国电机工程学报，2008，28(27):142－147.

［10］Theodoulidis T，Kriezis E.Series Expansions in Eddy Current Nondestructive Evaluation Models［J］.Journal of Materials Processing Technology，2005，161(5):343－347.

［11］于亚婷，杜平安，李代生.电涡流传感器线圈阻抗计算方法［J］.机械工程学报，2007，43(2):210－214.

［12］任吉林，刁海波，唐继红，等.涡流传感器提离效应的ANSYS模拟［J］.传感技术学报，2008，21(6):967－971.