Mathcad和MATLAB辅助高职《应用数学》教学之比较*
2011-10-20肖前军于钦临
肖前军于钦临
(1.湖南理工职业技术学院 湖南 湘潭411104;2.山东省寿光市第七中学 山东 寿光262706)
Mathcad和MATLAB辅助高职《应用数学》教学之比较*
肖前军1于钦临2
(1.湖南理工职业技术学院 湖南 湘潭411104;2.山东省寿光市第七中学 山东 寿光262706)
数学软件辅助教学是当前高职数学课程改革的主潮流。本文基于教育学和心理学理论,在介绍M athcad和M ATLAB的特点和通过实例比较二者在辅助《应用数学》教学过程中的具体应用的基础上,分析得出M athcad更适合数学学习基础普遍薄弱的高职学生的结论。
M athcad;MATLAB;高职;应用数学;辅助教学;比较分析
数学思想、方法和科学计算能力是高职学生适应未来岗位要求、培养可持续发展潜力的必备素质和基本能力之一。当前,高职院校在《应用数学》课程改革过程中普遍引入数学软件来辅助教学,其好处有:(1)能培养学生的科学计算能力,体现了科学与时俱进的精神。(2)解决了高职学生在数学学习过程中的最大困难——对数学推理和数学计算技巧的掌握。(3)可以节省出更多的时间用于加强最精华的内容——数学思想及其应用的教学。数学思想是数学的灵魂,是数学的精华,学生只有深刻理解数学思想后才能在解决专业问题时得心应手。
使用数学软件辅助教学好处很多,选取一款恰当的软件更能事半功倍。目前,在科技和工程界比较流行的数学软件主要有四个,分别是Maple、MATLAB、Mathcad和Mathematica,而在高职院校流行的软件主要是MATLAB和Mathematica。但我们在教学改革实践过程中发现,Mathcad更适合数学学习基础普遍相对薄弱的高职学生。笔者基于教育学和心理学理论,在介绍Mathcad和MATLAB的特点和通过实例比较二者在辅助《应用数学》教学过程中的具体应用的基础上,分析Mathcad辅助高职数学教学的优越性。
教育学、心理学理论依据
教育学 美国著名教育家布卢姆在“掌握学习”理论中指出:只要提供适当的先前与现时的条件,几乎所有人都能学会一个人在世界上所能学会的东西。根据维果斯基的“最近发展区”理论,只有较好地确定学生的“最近发展区”,才能循序渐进地将学生的“最近发展区”转化为现有的发展水平,从而有效地、最大程度地提高学生的知识和能力水平。因此,教学的任务之一就是正确地估计学生的已有发展水平和可能的发展水平,找到能使尽可能多的学生取得较大进步的方法与材料。
心理学 从现代认知心理学得知,只有适合学生认知基础和认知特点的教学内容、教学手段和方法才是最有效的;只有在考虑到学生现有知识水平的基础上确定学生的潜在水平,才能做到教学内容和教学深度是“必需”和“够用”的。因此,学生的数学认知水平是学生学好数学非常重要的因素之一。
Mathcad和MATLAB简介
Mathcad Mathcad是集文本编辑、数学计算、程序编辑和仿真于一体的一个交互式数学系统软件。其主要特点是输入格式与人们习惯的数学书写格式很近似,采用所见即所得的工作界面,还带有一个程序编辑器。其程序编辑器的优点是语法特别简单。Mathcad有三大“面向大众”的特点:一是Mathcad的数学式同平常文稿中的书写格式一样,因而形象、直观,便于阅读。用户可以按习惯的标准书写格式输入数学公式、方程组和矩阵,计算机能直接给出或数字或符号或图形的结果,用户无须考虑方法以及中间步骤。二是MathCAD生成的“电子书籍”中的指令、函数、图形都是“活的”,指令中的任何参数变化都会使相应的结果发生改变。三是灵活的“便笺”式文字处理功能,可以输入文本或对图形进行注释和说明,从而生成各种报告和科学论文。
MATLAB MATLAB是一款高性能的科技计算软件,广泛应用于数学计算、建模、仿真和数据分析处理及工程作图,是数值计算的先锋,具有多样的、专业的工具包。它提供的工具包覆盖信号处理、系统控制、统计计算、优化计算、神经网络、小波分析、偏微分方程、模糊逻辑、动态系统模拟和符号运算等领域。其功能强大,几乎能解决一切数学问题,其他软件能做的工作它几乎都能作。因此,它是科研人员和师生进行科学研究的得力工具,更是高质量新产品研究、开发和分析的主要工具之一,也是高校数学、工程等多个学科各类课程的辅助教学工具。
实例比较
基础计算 以极限、导数、积分方面的实例来说明,见表1。

表1 基础计算实例比较表
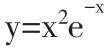
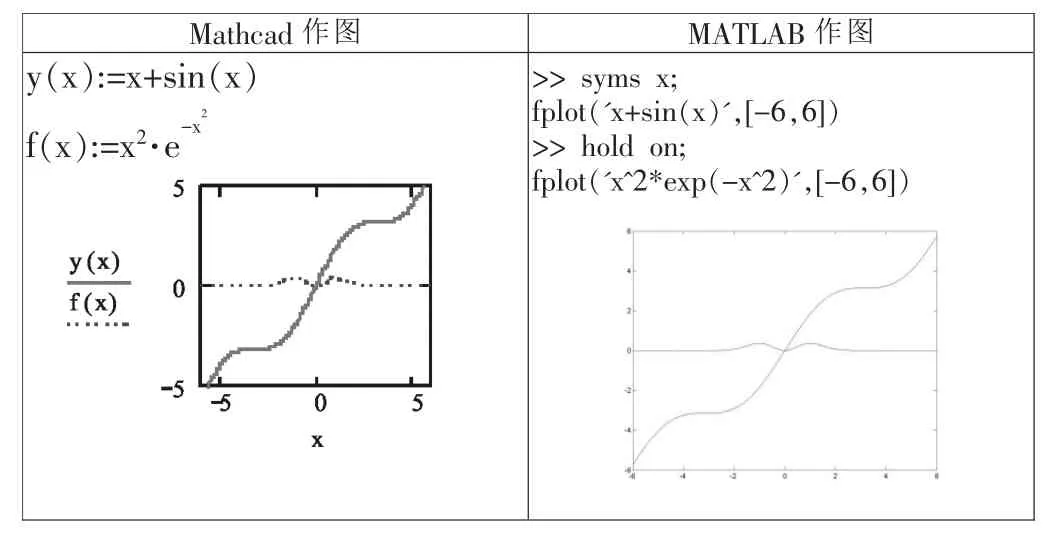
表2 函数作图实例比较表
案例应用 案例:已知某产品的边际成本和边际收入分别为C'(x):=x2-4x+6,R'(x):=105-2x,且固定成本为100,其中x为销售量。当销售量为多少时有最大利润?最大利润是多少?解题过程比较见表3。

表3 案例解决过程比较表
编程分析 实例:用梯形法和抛物线法计算的近似值。程序设计比较见表4。

表4 程序设计比较表
分析和结论
数学软件辅助教学正越来越广泛地被高职数学教育工作者所接受。为更好地发挥数学软件辅助教学的功效,基于教育学和心理学理论,我们认为,选取适合高职学生“学情”的数学软件非常重要。因此,我们首先要了解高职学生的具体“学情”:(1)高职学生的数学认知水平普遍偏低。具体表现在:数学认知基础不扎实;数学认知结构不良;数学认知加工水平较低;知觉与思维水平低;数学学习的迁移能力不佳。因此,高职学生对超出自身数学认知能力的新事物表现出较低的接受水平。(2)高职学生的“最近发展区”普遍难以清晰界定。维果茨基认为,每个学生都有两种发展水平,一是现有水平,二是潜在水平,现有水平与潜在水平间的发展区域称为“最近发展区”。对高职学生而言,他们的这两种发展水平存在两个显著的特点,一是发展水平普遍偏低,二是发展水平参差不齐。两种发展水平越是偏低就越难清晰界定最近发展区,加之两种发展水平参差不齐,这无疑更增加了界定难度,因而只能采取适度就低不就高的方法来解决。
因此,只有考虑到学生的数学认知水平的现实,才能使教学真正有效;只有正确估计学生的己有发展水平和可能的发展水平,才能使学生已有的学习经验对现在的学习产生积极的影响。基于此,在选择数学软件辅助教学时,应该立足于学生较低的现有发展水平,使得软件的操作形式更接近于高职学生现有的认知水平。通过前文对Mathcad和MATLAB的特点的介绍,以及它们在辅助教学过程中实际应用的比较,可以明显得出:Mathcad在辅助高职数学教学上有一定的优势。主要体现在:
Mathcad的功能定位适应高职学生 首先,其功能足以满足高职学生的要求。其次,Mathcad的大众化特点使其不要求用户具有高深的计算机知识,在程序设计上基本不需要计算机程序语言基础,更易于学生接受和使用。
软件的操作形式更接近高职学生现有的认知基础 其一,MathCAD中输入的数学式子的格式完全与学生原有认知对象相一致,即输入的式子和现实书写的式子完全一致。其二,计算过程完全与学生原有认知过程相一致,即求解过程和得到的结果与现实的求解过程及其结果完全一致。其三,程序设计的核心和难点——算法的设计——在形式上基本与现实书写的式子一致。
软件的操作复杂性大大低于MATLAB其一,MathCAD采用所见即所得的界面形式,即生成的指令、函数、图形都是“活的”,其中的任何参数都可以直接修改,相应的计算结果也随之发生改变。而MATLAB必须重新定义参数或增加相应的命令,运行后才能得到相应的结果。其二,在MathCAD同一界面中,可以完成所需要完成的全部工作,包括基础计算、图形(及其注释)输出、程序设计、文字处理等,可以生成各种报告和科学论文,而MATLAB无法在同一工作界面中同时完成上述工作任务。
基于上述分析,我们认为,Mathcad辅助高职数学教学更符合高职学生的“学情”,更能满足认知基础普遍偏低的高职学生在“做”中学习数学的要求,进而使高职学生学数学的过程成为一个建构知识的过程,而不是一个复制知识的过程,达到有机地发展学生能力的目的。
虽然我们认为Mathcad在辅助数学教学上比MATLAB更适合于高职学生,但Mathcad也有一定的局限性。MathCAD在对待数值计算、符号分析、文字处理、图形能力的开发上,不以专业水准为追求,而尽力集各种功能于一体。对需讲究精度、速度、算法稳定性的数值计算问题和需经复杂推理的符号运算问题,都不是MathCAD所致力解决的。因此,对于更高层次的学习要求,就需要功能更为强大的数学软件,如MATLAB。
[1]肖前军,周金玉,欧阳章东,邓总纲.高职数学差异化教学的策略[J].职业教育研究,2010,(1):12-13.
[2]周金玉,邓总纲,欧阳章东,肖前军.应用数学[M].北京:北京理工大学出版社,2008.
[3]肖前军,周金玉,欧阳章东,邓总纲.Mathcad在导数计算中的应用与问题解决[J].职业,2009,(10):46.
[4]周开利,邓春晖.MATLAB基础及其应用教程[M].北京:北京大学出版社,2007.
[5]姜华,李西君.试论掌握学习教育思想在开放教育教学中的应用[J].教育与职业,2009,(3):98-99.
[6]王文静.维果茨基“最近发展区”理论对我国教学改革的启示[J].心理学探新,2000,20(2):17-20.
[7]谢全苗.思维的“最近发展区”的开发与利用[J].数学通报,2004,(8):15-18.
[8]豁祖顺.数学问题解决与学生数学创造力发展的实证研究[J].教育与职业,2006,(18):106-108.
[9]郝黎仁,李宝麟,等.Mathcad2001及概率统计应用[M].北京:中国水利水电出版社,2002.
G712文献标识码:A文章编号:1672-5727(2011)09-0169-02
湖南省教育科学规划项目《高职院校学生自我素质教育理论框架及实施范式研究》(项目编号:xjk08czc037);湖南理工职业技术学院科研基金项目《模块化模式下高职数学教学的差异化评价体系的构建与实践》(项目编号:lgy09y004)
肖前军(1978—),男,湖南湘潭人,硕士,湖南理工职业技术学院讲师,研究方向为分形几何、生物信息学及高职数学教育。
