基于AutoCAD VBA的摆线齿锥齿轮实体三维仿真的实现
2011-10-20王强锋李海宁陈玉明陈超锋
王强锋 杨 勇 李海宁 陈玉明 陈超锋
(①西北工业大学机电学院,陕西西安 710072;②常州大学机械与能源工程学院,江苏常州 213016;③常州贝斯塔德机械科技有限公司,江苏常州 213016)
AutoCAD的三维模型支持创建线框模型、曲面模型和实体模型。对于较为复杂的实体可以通过对简单实体做布尔运算(并集、差集、交集)找出它们相重合的部分来创建。摆线锥齿轮的齿面是复杂的不可展空间曲面,不能用简单的实体造型方法形成,在AutoCAD中只能从平面冠轮展成加工原理出发进行实体建模,建模过程中生成的实体对象之间的关系如图1所示。
1 摆线齿锥齿轮实体建模原理
依据产形轮原理,把实际刀具运动轨迹看成产形轮,再与齿坯做范成运动。首先要模拟出产形轮的一个轮齿,产形轮为刀盘上切齿刀刃运动轨迹包络成的假想齿轮,摆线齿锥齿轮的加工过程又是刀盘、摇台、齿坯三者运动的合成,有必要确定三者间的基本运动关系。
第一个基本运动:摆线齿锥齿轮加工时刀盘一方面绕摇台轴线公转,另一方面又绕自身轴线自转,刀盘和摇台的回转轴线相平行。当刀盘和摇台回转时,它们就相当于1个以ρ为半径的滚圆,在1个以ρ0为半径的基圆上作纯滚动。刀盘相对于摇台的运动,相当于以ρ0为半径的滚圆在半径为ρ的基圆上作纯滚动,若假定刀盘和摇台的回转角速度分别为ω0和ωp,则满足 ω0/ωp= ρ0/ρ=Z0/Zp。其中 ρ0和 ρ分别为形成长幅外摆线的基圆半径和滚圆半径,Z0和Zp分别是刀盘的刀头数和产形轮的齿数。
在刀盘和摇台转动的过程中,刀刃直线与产形轮的分度平面的交点的轨迹形成了长幅外摆线,而刀具截面沿该轨迹扫描出的齿面形成了产形轮的齿廓面:外切刀片刀刃形成产形轮凸齿面加工摆线齿锥齿轮副的凹齿面;内切刀片刀刃形成产形轮的凹齿面加工摆线齿锥齿轮副凸齿面。外切刀盘的旋转轴线与内切刀盘的旋转轴线不重合,这种设定使加工出的克林贝格锥齿轮的凸齿面和凹齿面的齿线的曲率半径不一样,形成了克林贝格齿轮鼓形齿的特点。
第二个基本运动:刀盘和摇台各自运动复合成的假想产形轮和齿轮坯的旋转,包络产生被切齿轮轮齿的范成运动。设定被切小齿轮转速为ω1,产形轮转速为 ωp,当切削小齿轮时,并满足 ωp/ω1=Z1/Zp=sinδ1,Z1和δ1为小齿轮齿数和节锥角。
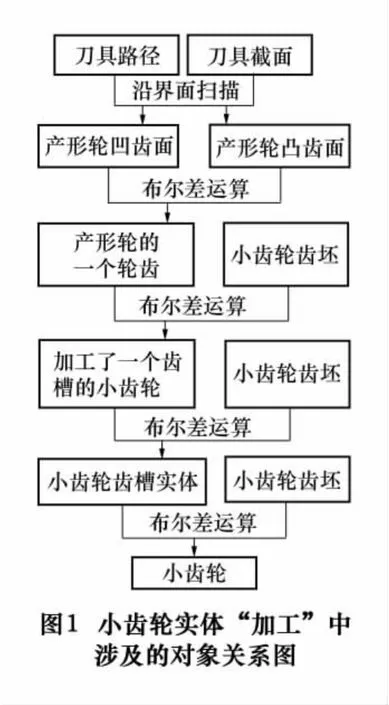
2 摆线齿锥齿轮详细建模过程
在锥齿轮建模中,需要用到几何设计模块的部分计算结果,这些计算结果全部以函数中调用参数的形式传递,其中主要的传递参数包括小齿轮齿数Z1,大齿轮齿数Z2,大齿轮节锥大端直径d02,齿轮齿宽b,刀具的法向模数mn,小齿轮的径向变位系数χ1,小齿轮的切向变位系数χt1,铣齿机机床型号,刀盘刀齿组数Z0,刀盘发生圆半径r0,外刀盘的偏心距Exb,刀具的压力角 α0。
2.1 绘制锥齿轮齿坯实体
绘制锥齿轮齿坯的基本方法是确定齿坯与摇台平面的关系,计算齿坯轴截面上的控制点,生成的齿坯轴半截面面域后绕齿坯中心轴线回转拉伸得到齿坯实体。
图2显示为大小齿轮齿坯半轴截面和摇台平面的位置,大小齿轮齿坯半轴截面与产形轮分度圆平面垂直。锥齿轮齿坯在铣齿机上装夹时必须保证轮坯的分度锥母线和其轴线的交点与摇台回转平面的中心重合,且在摇台平面内的分度锥母线与齿坯轴线构成的平面应该与摇台平面是垂直的。齿轮齿坯轴截面的控制点可由几何设计模块的结果计算出其坐标值。需要调用的参数包括节锥角δ1和δ2,节锥大端直径d01和d02,齿轮齿宽b,径向变位系数 χ1,切向变位系数 χt1。摆线齿锥齿轮的大齿轮和小齿轮的变位量之和为零,小齿轮取正值,大齿轮取负值。生成小齿轮齿坯的部分代码如下:


2.2 刀具路径的形成
刀具路径可以根据长幅外摆线的形成原理通过编程方式将其绘出。即把曲线划分为一系列极微小的曲线段,每段用一小段直线代替,以大量的直线段来模拟曲线,当精度较高时,模拟的直线段能很好地逼近真实曲线。另外也可以先计算出曲线上的控制点,然后利用AutoCAD提供的绘制样条曲线的命令,让样条曲线通过这些控制点从而绘制出曲线。这两种方法都需要计算出控制点的位置,前一种模拟的“曲线”实际是有大量小段直线构成的多段线,曲线的精度无法保证;后一种样条曲线必须计算出起点和终点的切点坐标,计算误差较大。解决的方法可以使用AutoCAD中内置的样条化多段线类型,把生成的多段线转化为样条化多段线(即样条曲线)。AutoCAD VBA中没有内置的多段线转化为样条化多段线的函数,解决方法是把编辑生成的多段线作为选择集对象,然后用SendCommand方法执行发送命令行命令方式转化为样条曲线,可用一个自定义函数BladePath表示:

刀具路径的建模可以抽象为图3所示,刀盘绕摇台轴线Op按逆时针回转θ角度值(取微量小)的同时,必定还绕自身轴线Oq逆时针回转(ρ/ρ0)θ角。建模时,可以抽象为两条直线的运动:一条是摇台轴线Op与刀盘自身轴线Oq的连线OpOq(长度等于刀盘发生圆半径r0);一条是刀刃的计算点M点与刀盘自身轴线Oq的连线MOq(长度等于刀位Ex),当OpOq绕轴线Op逆时针回转 θ角度值,MOq逆时针回转(ρ/ρ0)θ角。由此可以得到一系列的刀刃的计算点M点的坐标值,作为生成多段线的控制点,控制点的数量只要保证刀具截面沿生成的刀具轨迹曲线能完整地穿越产形轮的齿宽长度,编程时可声明一个多段线三维坐标动态数组,采用了自定义函数ArraySize控制控制点数组的大小,从而保证得到有效长度的长幅外摆线所代表的刀具路径。以下是生成模拟刀具路径所用的多段线的函数代码:


2.3 绘制产形冠轮单个轮齿实体

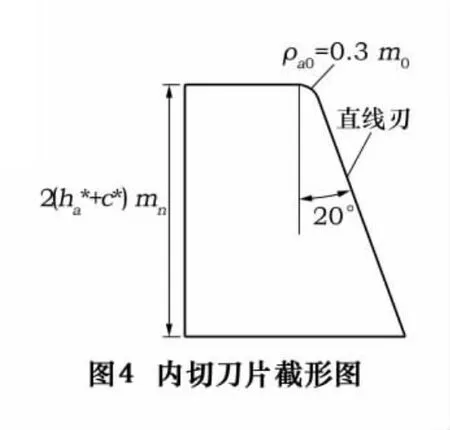
绘制产形轮的2个基本对象:一个是刀具路径,另一个是刀具截形。刀盘的切削刃为直线刃,且刀盘的切削刃垂直于摇台平面。以绘制与左旋小齿轮啮合的右旋产形轮轮齿为例,外切刀片刀刃形成产形轮的凸齿面加工摆线齿锥齿轮副的凹齿面;内切刀片刀刃形成产形轮的凹齿面加工摆线齿锥齿轮副凸齿面。已知外切刀片的截形如图4所示,其中刀顶圆角半径 ρa0=0.3m0,刀具齿高h=2+c*)mn,刀具齿形角 αn=20°。
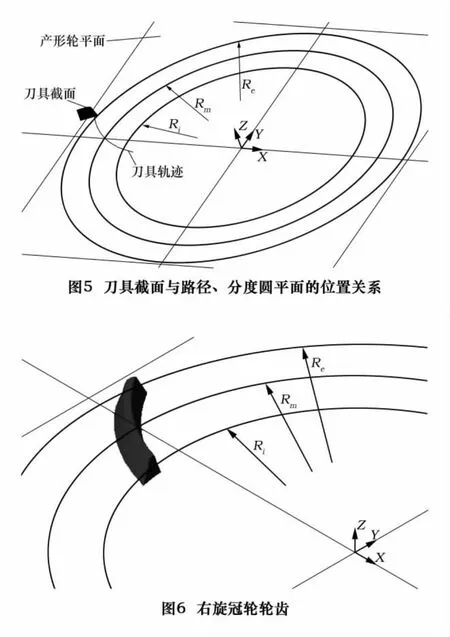
由于刀顶圆角为一段过度圆弧,宜采用生成多段线后再设置刀顶处两段直线的凸度,封闭多段线生成一个面域对象即可。该面域与刀具扫描路径所在产形轮分度圆平面垂直。此时还需计算出直线刃处与产形轮分度圆平面的交点位置即刀具沿刀具路径扫描时刀具上的参考点位置,当切削小齿轮时,若小轮采用正变位系数为χ,刀具参考点位置为刀具截面中线下移χ1mn后与直线刃的交点所在位置,截面与刀具路径、产形轮分度圆平面的位置关系如图5所示。
实际建模时将外切刀片截面和内切刀片截面分别沿刀具路径扫描,生成产形轮的凸齿面实体和凹齿面实体,然后将凸齿面实体绕摇台轴线逆时针回转冠轮法向分度圆齿厚对应的圆心角,再将凹齿面实体和凸齿面实体做布尔交运算,截取冠轮在外锥距与内锥距之间有效齿线长度方向的部分,即可得到完整的冠轮轮齿。如图6所示为右旋冠轮轮齿。
2.4 摆线齿锥齿轮三维实体的生成
编程时关键是判断小齿轮坯与产形轮旋转到哪个位置的时候,两者之间就没有重叠部分,即已切出一个完整齿槽。图7为切制出一个齿槽的小齿轮轮坯。产形轮“切制”小轮齿坯在AutoCAD可表现为两者在一些列特定位置的布尔差运算,当获得带有单个齿槽的齿坯时,用未加工的完整齿坯与这个带有单个齿槽的齿坯作布尔运算的减操作,可得到一个齿槽的实体,如图8所示。可再用一个齿坯每隔360°/Z与齿槽实体作布尔减运算,可以得到要加工出的齿轮,如图9所示。

2.5 实体建模过程中应考虑的问题
上述的齿轮建模过程都是以右旋产形轮切削左旋小齿轮齿坯为例说明。实际建模中还要考虑到右旋大齿轮、右旋小齿轮、左旋大齿轮三者的建模。这4种齿轮的建模原理一样,所以编程中可使用相同的函数,只需更换参数即可。
大小齿轮轮坯建模中无需考虑左旋、右旋齿轮之分,这是建模过程中完全相同的部分。在产形轮轮齿的建模过程中存在不同的部分:(1)刀具截形相同,直线刀刃的偏向不同。用内切刀片刀刃面域生成凹齿面;用外切刀片刀刃面域生成凸齿面。(2)刀具截形与产形轮平面的位置不同。小齿轮采用正变位,刀具截形面域拉伸参考点的位置与产形轮平面的距离增加χ1mn;大齿轮采用负变位,刀具截形面域拉伸参考点的位置与产形轮平面的距离减少χ1mn。(3)刀具路径的旋向不同。图3中生成刀具路径的原理为OpOq和MOq分别绕Op和Oq同向逆时针旋转,当OpOq和MOq均在X坐标轴上侧时,生成右旋刀具路径;当OpOq和MOq均在X坐标轴下侧时,生成左旋刀具路径。
4种齿轮的建模过程都是以摇台回转轴线与产形轮分度圆平面交点即啮合齿轮副的轴线交点为Auto-CAD中默认世界坐标系的原点,产形轮分度圆平面为世界坐标系的XY轴所在平面。创建刀具路径即长幅外摆线就在世界坐标系的XY轴所在平面上。当绘制齿轮齿坯半轴截面和刀具截面时,均在XY轴所在平面的垂直平面上。此时需要变换坐标系,编程时由此引入了GetToolUCS函数,代码如下:

GetToolUCS函数仅把用户坐标系的XY轴平面变换到世界坐标系的XZ轴平面上,其中的齿轮齿坯半轴截面可直接在当前绘图平面绘制。而刀具截面在沿刀具路径扫描时必须保证与刀具路径起始点切线方向垂直,此时起始位置与当前平面成一定角度,编程中计算出这一角度,用Rotate3D函数旋转即可。
3 结语
利用冠轮展成加工原理编制摆线锥齿轮实体建模模块。该模块模拟机械式机床的切削加工过程,仿真后获得真实的三维实体模型软件系统完全参数化简化了锥齿轮的建模能有效地获得锥齿轮实际加工的仿真结果,观察齿面的齿形几何结构以及锥齿轮的根切等,从而能够及时地修正切齿调整参数。锥齿轮建模获得锥齿轮实际加工的仿真结果后,可在AutoCAD的动态观察器任意位置或角度观察齿面的齿形几何结构以及锥齿轮的根切情况,预先了解加工结果。
[1]董学朱.摆线齿锥齿轮连续分齿法铣齿原理的研究[J].机械传动,1999,23(2):29 -30.
[2]董学朱.延伸外摆线锥齿轮切齿调整计算法的改进[J].机械传动,1997,21(4):41 -47.
[3]张帆,郑立楷,王华杰.AutoCADVBA开发精彩实例教程[M].北京:清华大学出版社,2004.
[4]张帆.Auto CADVBA二次开发教程[M].北京:清华大学出版社,2006.
