结合面切向动态特性参数的改进Levy法识别及验证研究*
2011-10-20郭丹枫胡小秋王志勇
郭丹枫 胡小秋 王志勇
(南京理工大学机械工程学院,江苏南京 210094)
固定结合面的动态特性对机床整机动态特性有重要影响。一直以来,许多学者都致力于研究结合面的动态特性参数及其影响因素,出现了众多测试装置并获得了大量特性参数数据[1-3]。但到目前为止,这些测试数据的有效性仍没有统一的评价标准,尤其对阻尼系数的评价存在很大不足,限制了测试数据在实际工程中的应用。因此,结合面动态特性参数识别方法及测试数据有效性评价的研究,对建立可用的结合面动态特性参数数据库以及整机动态特性的预测都有重要意义。本文提出了一种基于Levy法的改进的参数识别方法,并利用ANSYS对识别参数进行了有效性验证。
1 测试装置及力学模型
结合面切向动态特性测试装置如图1所示,上、下板之间放入垫片,以模拟结合面,并用螺钉连接;调节螺钉的扭矩T可以改变结合面的载荷F。同时,测试中控制上、下板的材质和粗糙度相同,以及垫片上、下表面的粗糙度相同,因此垫片上、下表面结合面的切向动态特性一致。在切向激振力f的作用下,可将测试装置简化为图2的力学模型。
根据力学模型,将上板的振动微分方程表示为
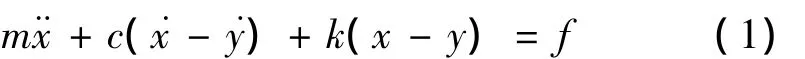
式中:m为上板的质量;k和c分别为结合面的动刚度和阻尼系数;x和y分别为上、下板的位移。
式(1)两边分别减去m¨y项,经变换后得到频响函数H(ω):
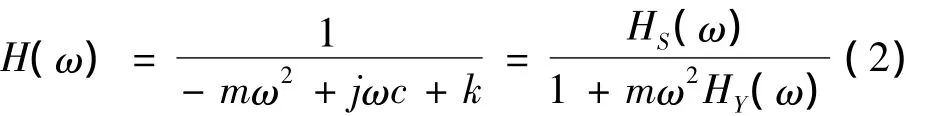
式中:HS(ω)=[X(ω)-Y(ω)]/F(ω),为上、下板位移频响函数矢量差;HY(ω)=Y(ω)/F(ω),为下板位移频响函数。

2 参数识别的Levy法及其改进
式(2)中的H(ω)是由质量为m、刚度为k以及阻尼为c组成的等效单自由度系统频响函数。对单自由度系统频响函数特征参数的识别通常采用的方法有峰值共振法、半功率带宽法以及导纳圆法。但这些方法都会因测试中峰值的偶然误差及作图误差等的影响而使参数识别的精度降低。因此,为了提高结合面动态特性参数的识别精度,本文采用改进的有理分式多项式法(Levy法)对结合面参数进行识别。
Levy法参数识别的数学模型是采用频响函数的有理分式形式,由于未使用简化的模态展式,理论模型是精确的,因而有较高的识别精度[4]。但在实际识别中发现,由于Levy法是对全频率段内的测试数据进行拟合,因此当测试过程受外界噪声干扰时,即使对同一组测试数据,如果选取的频率区间不同,其拟合误差也会不同,从而导致参数值不一致,尤其是阻尼值存在较大的误差。
为了提高参数识别的精度,测试中对Levy法进行了改进,改进后的参数识别过程如图3所示。该方法可以同时识别出刚度值和阻尼比,并通过比较前后阻尼比的识别结果,不断调整频率段范围,直至阻尼比满足要求,并以最后一次识别得到的刚度和阻尼比作为测试数据。通过在MATLAB中编制程序。该方法可以实现在受干扰较小的频率段内对参数进行识别,并且识别精度大幅提高。

由表1可知,改进前的Levy法在不同频率区间识别得到的阻尼值差别较大,而改进后的Levy法识别得到的阻尼值精度较高。图4为用改进后的Levy法拟合的频响函数曲线与实测曲线。由图可知,改进后的Levy法拟合的频响函数曲线与实测曲线吻合较好。可以得出,通过该方法不仅可以识别刚度值,同时也能得到准确的阻尼值。其中对阻尼值的识别精度高于其他的识别方法,是该识别方法最大的优点。

表1 改进前后Levy法的阻尼值识别比较


表2 不同MATRIX27单元数量实测频率与计算频率比较
3 结合面动态特性参数验证
通过识别得到的特性参数是否真实地反映了结合面的动态特性,需要进行验证。本文通过运用ANSYS有限元分析软件将识别参数代入到分析模型中,并进行动力学分析,以实现对识别参数的有效性验证。但在有限元分析中,不同的处理方法会导致结果不一致,这也使得到目前为止,对结合面特性参数的有效性没有统一的评价标准。
为了获得可靠的有限元模型,此处分析了弹簧阻尼单元的数量及其分布对结合面动态特性计算的影响。通过测试得到直径为10 mm的垫片在15 kN载荷下的切向动刚度值为442 N/μm,共振频率为1 017 Hz。现以该测试数据和模型为例,分析运用ANSYS对结合面进行动态特性验证时,不同的处理方法对计算结果的影响。
3.1 MATRIX27单元数量对计算结果的影响
根据图1的测试模型,在ANSYS中建立如图5所示的有限元模型。选择MATRIX27单元作为结合面的弹簧阻尼单元,并在结合面间依次设置1、2、4、8、16、32及64个MATRIX27单元,以分析不同的弹簧阻尼单元数量对计算结果的影响。根据MATRIX27单元特性及并联弹簧阻尼单元的等效原理,在ANSYS中设置每个MATRIX27单元切向(X和Y方向)的刚度值分别为442 Nμm,221 Nμm,110.5 Nμm,55 Nμm,27.6 Nμm,13.75 Nμm 及6.9 Nμm;并设置MATRIX27单元法向(Z方向)的刚度值为4 420 Nμm,其余设置为0(不考虑绕轴旋转刚度的影响)。此外,计算过程中对下板的底面施加全约束,并在切向施加1 N的简谐激振力,设置强制计算频率范围为0~1 500 Hz,同时设置分析类型为谐响应分析,经计算后得到的频率值如表2所示。
从表2可以看出,在结合面间设置的MATRIX27单元数量越多,计算值越接近测试值。但随着单元数的增加,ANSYS插值计算的次数也会增加,插值计算伴随着舍入误差,过多的插值计算将使舍入误差的累积量增大,反而导致计算精度及效率降低[5]。因此,MATRIX27单元数量并不是越多越好,应该在保证计算效率及精度的基础上,合理选择MATRIX27单元数量。

在综合比较了不同单元数对计算精度及效率影响的基础上,本文选择16个MATRIX27单元对结合面的切向动态特性进行验证。
3.2 MATRIX27单元分布位置对分析结果的影响
MATRIX27单元在结合面上不同的布置是否会对计算结果产生影响,这也是进行结合面动态特性计算需要解决的问题。将MATRIX27单元设置在如图6所示的4种不同位置(图中每1个黑点代表1个MATRIX27单元的位置分布),得到的计算结果如表3。

表3 不同MATRIX27单元分布的实测频率与计算频率比较
从表3可以得出,MATRIX27单元分布不能过于集中,也不能过于分散,否则会造成计算结果与实际测试值的误差增大。如图6b的分布会使计算误差达到53.15%。合理的做法应该是使MATRIX27单元尽可能均匀分布于结合面上,如图6a所示,这将有助于减小误差,提高计算精度。
综上所述,在利用ANSYS对结合面动态特性进行验证时,不仅要合理选择单元数目,而且应尽量使单元均匀分布在结合面上,只有这样的处理方式才能准确地对结合面的动态特性进行检验。

4 应用
为进一步说明改进的Levy识别法的有效性及验证模型的可靠性,分别对直径为10 mm的垫片在7.5 kN、15 kN及22.5 kN载荷时的测试数据进行识别,并将识别参数代入ANSYS验证模型中,其共振频率及峰值比较如表4、5所示。

表4 实测频率与计算频率比较

表5 实测峰值与计算峰值比较
由表4、5可知,实测频率与计算频率误差在6%以下,说明了对刚度识别的精度较高。而峰值误差体现了对阻尼值的识别精度,虽然峰值误差为50%左右,但由于阻尼识别的复杂性[6],其他的识别方法得到的阻尼值误差往往在一个数量级以上。因此,50%左右的峰值误差说明了该方法对阻尼值的识别精度较高。
5 总结
(1)对Levy法进行了改进,通过对阻尼比的循环迭代完成参数识别,有效避免峰值偶然误差及其他噪声对测试数据干扰的影响,具有较高的识别精度。
(2)在利用ANSYS对结合面动态特性参数进行验证时应合理选择弹簧阻尼单元数量,并将其均匀布置在结合面上,否则会使计算结果出现较大偏差。
(3)本文介绍的结合面动态特性参数识别及验证方法,不仅为结合面动态特性参数的评价提供了参考,同时也可用于结合面动态特性的准确预测,具有较高的工程应用价值。
[1]赵韩,陈奇,黄康.两圆柱体结合面的法向接触刚度分形模型[J].机械工程学报,2011,47(7):53 -58.
[2]Mao Kuanmin,Li Bin,Wu Jun,et al.Stiffness influential factors -based dynamic modeling and its parameter identification method of fixed joints in machine tools[J].International Journal of Machine Tools &Manufacture,2010,50:156-164.
[3]王立华,罗建平,刘泓滨,等.铣床关键结合面动态特性研究[J].振动与冲击,2008,27(8):125 -129.
[4]王济,胡晓.MATLAB在振动信号处理中的应用[M].北京:中国水利水电出版社,2006.
[5]张兴朝.基于有限元分析的模块化数控机床结构动态设计研究[D].天津大学,2001.
[6]孙亮,侯宏.阻尼识别的小波和EMD方法仿真对比研究[J].振动、测试与诊断,2008,28(2):164 -167.
