地球化学异常下限不同确定方法及合理性探讨
2011-10-19陈守余廖阮颖子
姚 涛,陈守余,廖阮颖子
(1.中国地质大学(武汉)地质过程与矿产资源国家重点实验室,武汉430074;2.中国地质大学(武汉)资源学院,武汉430074)
0 引言
周蒂[1]认为,较合理的异常圈定方法应该是:根据工作区的地质、地球化学及景观资料逐点估计地球化学背景值,再从观测数据中减去背景值及随机误差而圈定异常。这一认识说明,确定地球化学异常下限是一个很复杂的过程,对于不同的背景应该选择不同的异常下限。
对于1∶20万化探扫面数据,史长义等[2]在对已知的各种化探数据处理方法进行系统研究的基础上,吸收了EDA技术和滤波技术,开发出子区中位数衬值滤波(SAMCF)法。该方法很好地实现了不同子区采用不同的异常下限,但是在实际工作中其计算和成图过程都比较繁琐,并且只有在研究区面积足够大的时候使用该方法才能得到理想的效果。
为了更好的确定异常下限,圈定异常区域,笔者采用了按照不同背景分区采用不同的异常下限圈定异常。但是有一个问题,就是不同地质单元之间的等值线连接是十分不理想的。因此,笔者又尝试了另一种方法——归一化法[3],将原始数据经归一化处理后再计算异常下限。
此外,传统的地球化学异常下限计算方法(均值+K倍的标准离差)在K值的选择上存在一定的随意性。为了克服这一弊端,Cheng Q M(成秋明)等1994提出了含量-面积模式[4],首次将分形引入地球化学异常的判别,并且在加拿大取得了成功,在国内也引起了很大的轰动。
白银厂铜多金属矿田是具有很长开发历史的老矿山,由于计算机技术在最近十几年才得到普及和发展,所以前人在找矿过程中很少有机会或者根本就没有机会尝试现在的一些新技术、新方法。而传统方法圈出的异常很容易漏掉一些弱小的异常。由于各种原因(比如覆盖物比较厚),有时候在弱小异常处却隐藏着大矿,所以从某种程度上说漏掉弱小异常也就是漏掉了发现大矿的机会。
为了进一步开发该地区的矿产资源,笔者尝试应用新技术、新方法在白银矿区及外围圈定地球化学异常区域。本文在分别运用传统方法、归一化法和分形方法确定白银矿区及外围1∶5万水系沉积物Cu,Pb,Zn,Ag等4个元素的地球化学下限,对 异常区进行圈定,并将3种方法圈定的结果进行比较分析。
1 区域地质背景
区内地层从古生界到新生界多有出露(图1)。其中,寒武系—志留系属地槽型海相沉积(伴有火山碎屑沉积),泥盆系—第三系以内陆湖盆相沉积为主,第四系主为冲沟堆积。不同时代地层多以同构造线方向的断层相隔。
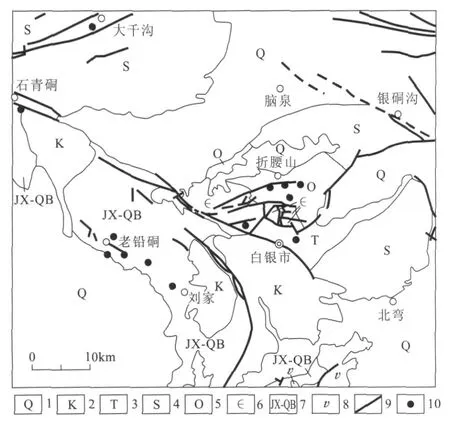
图1 白银矿区及外围矿产地质略图(据甘肃省有色地质三队资料修编)Fig.1 Geological stetch of Baiyin Mine Area and its periphery
侵入岩主要有花岗岩、斜长花岗岩、花岗闪长岩、石英闪长岩、辉绿岩、辉长岩、蛇纹石化橄榄岩等。岩浆作用分异连续完整,基性、中基性、中性、酸性火山岩发育齐全。火山岩的分布受古断裂的控制[6]。以早古生代海相火山岩最为发育,其在空间展布上与区域构造线方向一致,呈NW-SE向带状分布。白银厂矿田的火山作用以裂隙喷溢为主,局部伴有中心式喷发[7],以熔岩为主,火山碎屑岩类相对较少。
白银矿区现已发现的矿床主要有折腰山、石青硐、老铅硐、小铁山、四个圈和铜厂沟等。其中,折腰山矿床规模最大。
2 区域地球化学特征
白银厂地区地貌景观为干旱荒漠,局部有黄土覆盖,气候干旱,干涸沟系发育,植被稀少。白银矿田处于高 Fe2O3,MnO,Na2O,CaO,低SiO2的环境中,在该环境中发育的成矿元素有Cu,Pb,Zn;伴生元素有Cd,Ag,As,Sb,Hg,Au,Bi,Mo,Ba等[8]。
从表1可以看出,研究区成矿元素Cu,Pb,Zn的平均值均明显高于全国均值和干旱地区平均值,中位数值也都明显高于全国中位数值;而伴生元素Ag的平均值则只是稍微高于全国平均值,中位数值则远低于全国中位数值。
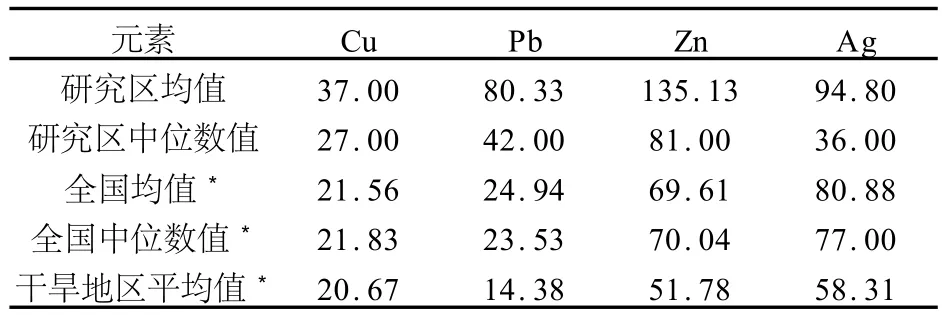
表1 Cu,Pb,Zn,Ag元素特征值表Table 1 Characteristic value of Cu,Pb,Zn,Ag
3 地球化学异常下限的确定
3.1 传统的统计学方法
长期以来,人们主要使用经典的统计学方法,以样品数据呈正态分布为假设前提,通过计算数据的统计学参数(如均值、中位数、标准离差等)对异常进行筛选和评价[9]。通常认为常量元素接近正态分布,而微量元素则接近于对数正态分布,但是在实际工作当中没有完全理想的数据满足正态分布或对数正态分布。因此需要我们对原始数据做一定的处理,使其满足正态分布或对数正态分布而又不失原 始数据的真实性。若原始数据满足正态分布,则直接用均值+2倍的标准离差得到异常下限;若原始数据不满足正态分布,则按照地球化学普查规范(DZ/T0011-91)的要求计算地球化学异常下限值:
(1)将原始数据转化为对数值,反复用(±2.5S)进行特高值和特低值剔除,直到其满足对数正态分布,将剩余数据进行统计。

其中,xi为剔除特高值和特低值后剩余的数据值;n为剩余数据的个数;C0为背景的对数;S为取对数后数据的标准离差;CA异常下限的对数。
2孕妈妈冬季少扎堆 冬季孕妈妈要尽量避免去人群众多的公共场所,减少被传染的几率。孕妈妈如果想去看场电影、逛超市,要尽量戴上口罩。
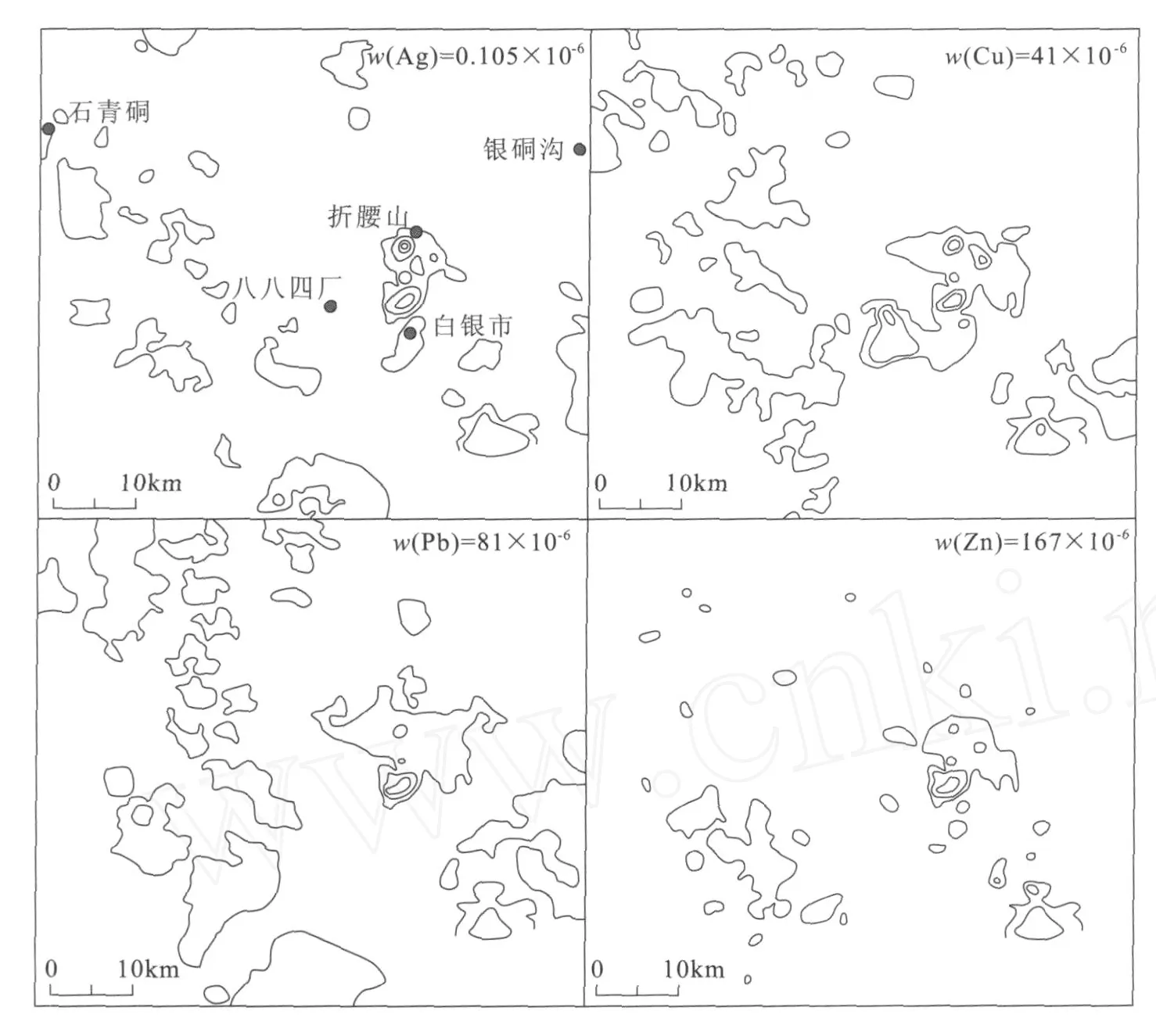
按传统方法圈出的异常(图2)主要集中在折腰山、白银市、八八四厂附近的区域,该地区为白银厂矿田所在区域。由于矿区高异常的压制作用,使得在其他地区几乎没有异常出现。
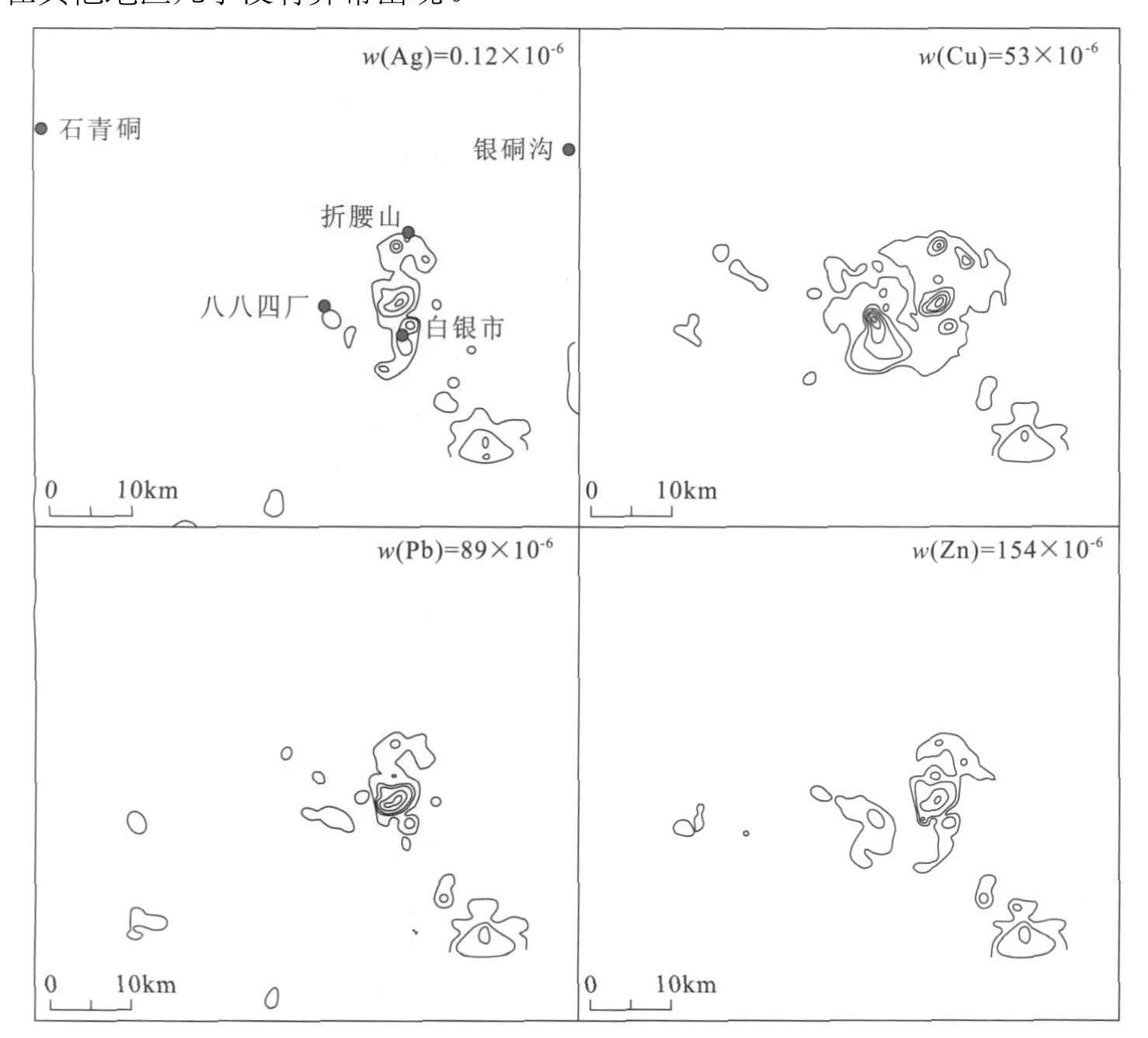
图2 白银矿区及外围Ag,Cu,Pb,Zn元素异常图(传统方法)Fig.2 Cu,Pb,Zn,Ag anomaly map of Baiyin Mine Area and its periphery(Traditional methods)
3.2 归一化法
陈明等在总结正确划分化探背景与异常的方法时认为,在进行背景与异常的识别之前,必须选择合理的方法校正采样和分析测试带来的误差[19]。由于研究区的样品数据是分4个区采集的,并且在该区有不同的地质背景,所以,笔者尝试用归一化法来处理原始数据。
归一化法是一种简单的数据调整方法,原理简单,实现起来也很方便,并且可以取得比较理想的效果。它适用于调整由于系统误差造成的不同分析批次间的数据“台阶”、不同地区背景值的差异造成元素数据置于一起研究时元素分布信息的弱化或强化等[3]。它是在知晓不同批次或不同空间分布的大块数据间的差异的前提下,为消除这样的差异而进行的简单的数据归一方法,是衬度法的一种改良方法,它用与元素实际分析值相近的视含量来代替在数值1附近波动的衬值,使得处理后的结果更直观,更易于理解和接受。
计算公式为:

式中:为第j个地质体中第i个样品的处理后的数据;Cij为第j个地质体中第i个样品的原始数据;为第j个地质体分析数据的平均值为整个样品的总平均值。笔者将归一化之后的数据用均值+2倍的标准离差(迭代剔值后)计算异常下限,圈定异常。图3为归一化法圈定的地球化学异常图,与图 2比较,在老铅硐附近地区出现了Cu,Pb,Zn的异常,符合客观情况,但在石青硐地区附近依然没有异常出现。
3.3 分形方法
Cheng Q M等认识到传统的确定地球化学异常方法存在局限性,并从分形的观点(地球化学背景和异常的形成是两个独立的过程)认为地球化学背景值和异常值具有各自独立的幂 指数关系,由此导致了一种多重分形分布。在此基础上,Cheng Q M等提出了确定地球化学异常的分形模型,含量-面积模型。
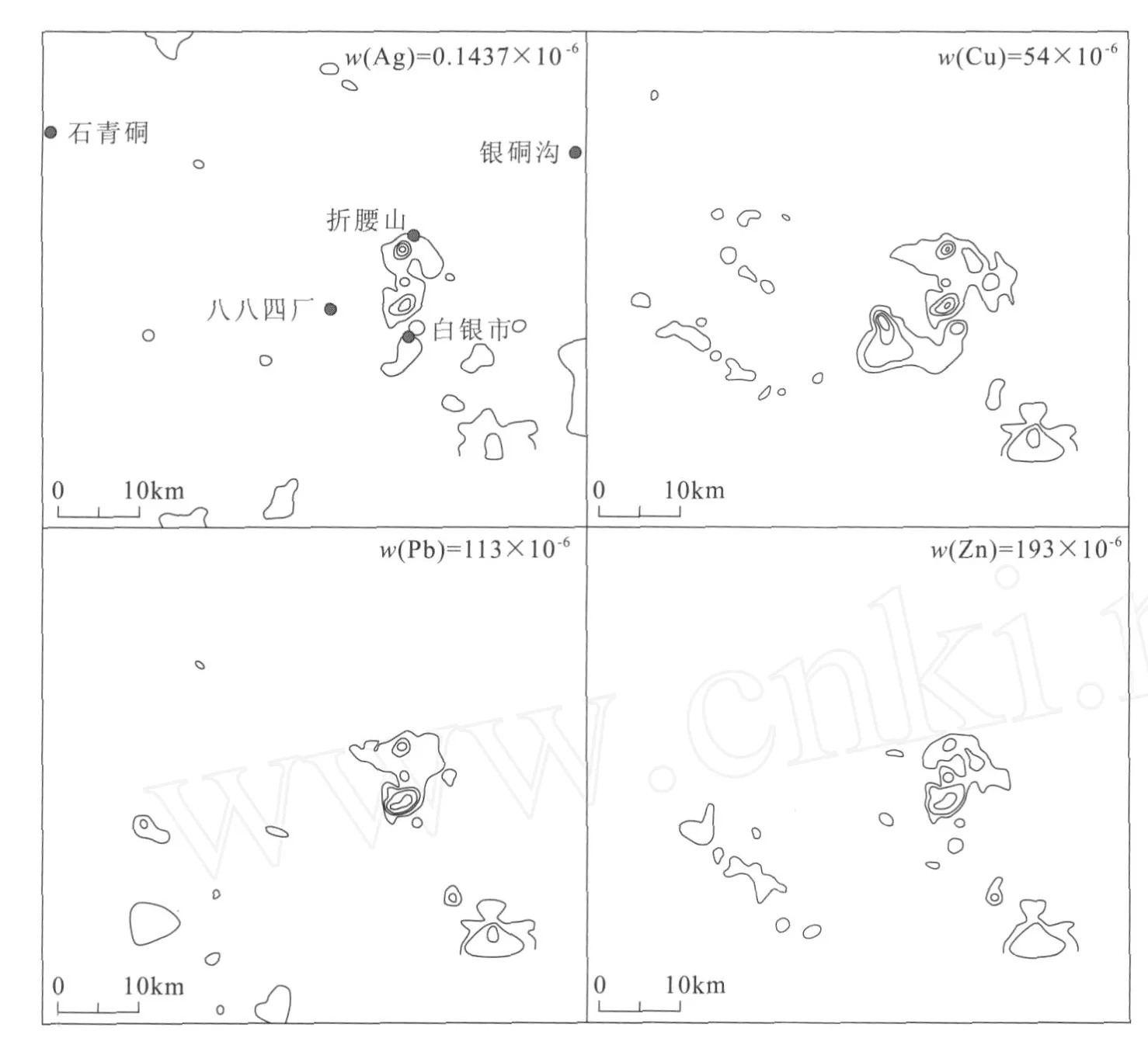
图3 白银矿区及外围Ag,Cu,Pb,Zn元素异常图(归一化数据后常规方法计算下限)Fig.3 Cu,Pb,Zn,Ag anomaly map of Baiyin Mine Area and its periphery(Normalization method)
Cheng Q M等提出的含量-面积模式是运用分形确定地球化学异常的第一次尝试[9]。笔者分别运用Cheng Q M等开发的Geodas软件和武汉中地信息有限公司开发的Mapgis软件尝试了用含量-面积模式来确定地球化学下限[11],但效果都不是很理想,出现了李长江等在《矿产勘查中的分形、混沌与ANN》一书中提到的问题:分辨率比较低,难以确定异常下限[9]。因此,笔者又尝试了分形求和法[12],该方法简单易行,而且效果也比较理想。研究中笔者将原始数据归一化消除系统误差之后,再运用分形求和法求异常下限。
分形求和模型:

式中,r为特征尺度;C>0为比例常数,D>0为一般分维数;N(r)=N(≥r)为尺度大于等于r的和数。
设地球化学元素的值
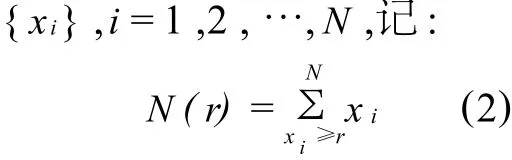
这里和式是对于所有满足xi≥r的xi求和。这样得到了一组N(ri)和ri(i=1,2,…,n 用最小二乘法求出斜率D的估计量,即为分维数;其散点大致分布在两段直线上,应采用分段拟合。为了提高界限点确定的客观性,在两个区间用最小二乘法进行回归时采用最优化方法确定界限点。其基本思想是,找出合适的界限点ri0,使各区间拟合的直线与原始数据点之间的剩余平方和Ei(i=1,2)在两个区间的总和E=E1+E2为最小。其中ri0是界限点,D1和D2分别为相应区间的斜率即分维数, 如图4所示,在石青硐(主要有铅、锌、铜矿)附近出现了弱小的异常,这是前面两种方法都没圈出的异常。 (1)图2中的异常主要集中在折腰山、白银市和八八四厂附近区域,由于高值异常的压制作用,在矿田以外的地区几乎没有异常出现;图3中的异常范围比图2大,在老铅硐地区出现了异常,这与实际情况相符;图4中的异常范围最大,几乎覆盖了所有的 矿化集中区,特别是在石青硐附近地区也出现了Cu,Pb异常。 图4 白银矿区及外围Ag,Cu,Pb,Zn元素异常图(归一化数据后分形方法计算下限)Fig.4 Cu,Pb,Zn,Ag anomaly map of Baiyin Mine Area and its periphery(Fractal method) (2)运用传统方法计算异常下限且原始数据未经归一化处理时,圈出的异常范围过小,可能是因为分区采样时造成的系统误差没有校正,不同地质单元采用了统一的下限值(高背景区的下限值)。归一化法刚好可以解决这个问题,使数据的可信度更高。但是对于归一化处理之后的数据用传统的(均值+K倍的标准离差)方法计算异常下限时,在K的大小选择上仍然受主观因素的影响比较大。如果取K=2的话,如图3所示,在石青硐地区附近没有出现任何异常;如果取K=1的话,则可以在该地区见到异常。当我们没有发现石青硐矿田时,我们的K值该怎么取呢?分形方法计算异常下限则可以很好地解决这个问题,因为按照分形的观点,地球化学背景和异常的形成是两个独立的过程,它们分别满足不同的幂指数分布,计算出来的结果更客观。 (3)分形方法计算异常下限虽然可以克服传统方法(均值+K倍的标准离差)在K值选择上受主观因素影响的弱点,圈定的异常更客观、更全面。但是,在实际工作中,对于分形模型的选择要经过不停的尝试才能得到比较理想的结果,而且要求化探工作者能够熟练地使用各种不同的软件,甚至还要求能够自己编写程序。所以,运用分形方法计算异常下限对人员素质的要求比较高。 (4)分形方法计算异常下限得到的结果(图4)虽然没有漏掉异常,但是同时也存在异常范围过大的问题,特别是如图4中的 Pb异常几乎占了全区的一半。因此,笔者认为可以将图3和图4叠合起来,综合分析圈定异常可以取得不错的效果。 (5)在实际化探工作中,对于地质背景比较复杂的地区,为了能够得到比较理想的结果,化探工作者必须考虑不同的地质单元的影响,并且采用比较合适的方法消除这种影响;在计算异常下限时要求根据实际情况采用合适的方法或多种方法相结合;圈定异常时,根据多种不同方法圈定的异常,综合分析应用,圈定成矿有利靶区。 [1] 周蒂.分区背景校正法及其对化探异常圈定的意义[J].物探与化探,1986,14(4):263-273. [2] 史长义,张金华,黄笑梅,等.子区中位数衬值滤波法及弱小异常识别[J].物探与化探,1999,23(4):250-257. [3] 刘大文.区域地球化学数据的归一化处理及应用[J].物探与化探,2004,28(3):273-279. [4] Cheng Q M,Agterberg F P,Ballantyne S B.The separation of geochemical anomalies from back-ground by fractal methods[J].Journal of Geochemical Exploration,1994,51:109-130. [5] 廖桂香,王世称,许亚明,等.白银厂矿区及外围区域地质背景、地球化学异常特征及找矿潜力[J].地质与勘探,2007,43(2):28-32. [6] 彭秀红.白银厂矿田构造-岩浆-成矿动态演化模式[D].成 都:成都理工大学,2007. [7] 王玉往,姜福芝,王明生,等.甘肃白银地区北部火山岩带的地质特征及其含矿性[J].地球化学,1995,24(增刊):55-65. [8] 任天祥,伍宗华,羌荣生,等.区域化探异常筛选与查证的方法技术[M].北京:地质出版社,1998. [9] 李长江,麻士华,朱兴盛,等.矿产勘查中的分形、混沌与ANN[M].北京:地质出版社,1999. [10] 陈明,李金春.化探背景与异常识别的问题与对策[J].地质与勘探,1999,35(2):25-29. [11] 李随民,姚书振.基于MAPGIS的分形方法确定化探异常[J].地球学报,2005,26(2):187-190. [12] 申维.分形求和法及其在地球化学数据分组中的应用[J].物探化探计算技术,2007,29(2):134-137.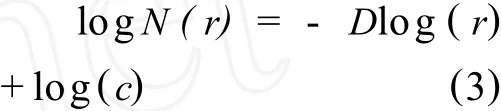
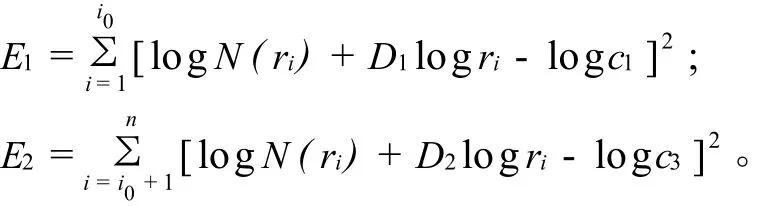
4 结果与讨论