基于QR分解的对称共轭梯度法成像算法*

马世文，王化祥

(天津大学电气与自动化工程学院，天津 300072)

电阻层析成像技术(Electrical Resistance Tomography，ERT)［1］是近年来发展起来的新型测量技术，由于该技术具有非侵入、无辐射、响应快、结构简单以及成本低廉等优点，在医学临床监护和工业测量等领域具有广阔的应用前景［2－4］。

如图1所示，电阻层析成像系统由三个部分构成:(1)获取被测物场信息的空间敏感阵列电极［5］，在交流电压/电流激励下，形成一个可从不同角度扫描被测对象的空间敏感场，物场内部介质分布或结构的运动变化对敏感场产生调制作用，使敏感阵列输出相应的信号;(2)数据采集与处理单元，实时快速地采集空间敏感阵列输出的反映被测物场介质分布状态的大量测量数据，完成相应的解调、滤波处理;(3)图像重建与物场特征参数提取单元，运用图像重建算法，依据处理后的数据，获得被测物场的图像及其变化的时间历程，实现被测物场内部介质分布可视化，并提取出与介质分布相对应的被测物场的特征信息。

图1 ERT系统示意图

为了便于ERT逆问题的求解，通过灵敏场的分析可将ERT的非线性物理模型线性化并归一化［6］，得出近似的线性基本方程如下

式中，z为n×1阶的测量数据矢量矩阵;S为n×m阶的灵敏度系数矩阵(归一化后的雅可比矩阵);g为m×1阶的灰度矢量矩阵;n代表独立测量电极对数;m代表场域的剖分单元数。

根据Geselowitz Sensitivity理论，ERT系统的近似敏感场分布如式［7－8］

其中，φi和φj分别为第i极板和第j极板施加电压V，而其余极板接地的电势分布。

共轭梯度法是一种基于最优搜索方向的迭代算法，同其他算法相比，它的收敛速度快，成像质量高。本文在共轭梯度法的基础上研究了对称共轭梯度法，进而通过QR分解实现了对称共轭梯度法的单步成像法。

1 共轭梯度法

共轭梯度法(Conjugate Gradient，CG)是共轭方向类算法中极为重要的一种方法。CG方法适合于系数矩阵为对称正定的情形。如果不考虑舍入误差，理论上它能保证最多迭代n步(n为方程组的阶数)，便可求得方程组Ax=b的精确解［9－10］。

定义:设A为一个N×N阶对称正定矩阵，p，q为两个N维向量，如果

则称向量p和q为相互A共轭。

定理:设A为一N×N阶对称正定矩阵，p1，…，pN为A共轭的N维向量，则此向量系必为线性独立［11］。

上述定理给出了A共轭向量系的线性独立性，而共轭梯度法的思想是只要依次沿着n个非零共轭方向进行搜索，便能达到其极小点，因此关键是如何构造A的共轭搜索方向。

在ERT图像重建中，由于灵敏度矩阵S既非正定又不对称，为保证重建算法具有较好的收敛性，必须对灵敏度矩阵进行正规化。

在式(1)两端同乘以灵敏度矩阵的转置ST，则

令 S'=STS，z'=STz。

取初始灰度值 g0为零向量，r0=z'－S'g0，p0=r0，依次按如下步骤循环迭代:

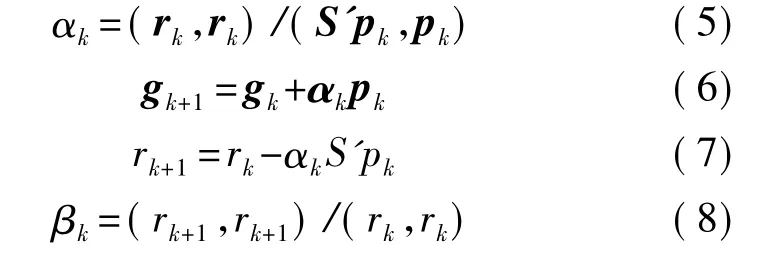
式中，pk为第k次修正方向，而各修正方向之间满足共轭关系

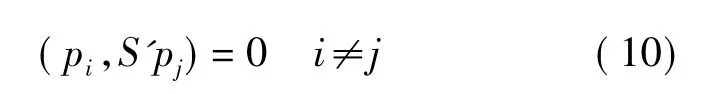
2 对称共轭梯度法SCG

ERT逆问题的求解具有不适定性，因此为得到逆问题的有效解，需补充解的附加约束条件以及先验知识。Tikhonov方法［12］是一种有效解决病态逆问题的方法，它已广泛应用于ERT的图像重建。

式(4)经过Tikhonov正则化后可转变为

式中:α为正则化因子，本文取0.01;I为同维单位矩阵。

本文在Tikhonov正则化的基础上提出了对称共轭梯度法［13］。对称共轭梯度法的每一步的迭代矩阵为对称矩阵。其具体实现过程如下:

令 S'=STS+αI，z'=STz，任取 g0，令 r0=z'－S'g0，p0=r0，迭代步骤如下:

将式(19)整理，有

3 基于QR分解的对称共轭梯度法

为了快速得到高质量的重建图像，在此提出一种新型的基于QR分解的单步对称共轭梯度成像法RQSCG。系数矩阵STS+αI为非奇异的矩阵，则存在唯一的正交矩阵Q和上三角矩阵R［14－15］，使得

经过QR分解后，式(10)可等价变化为

经过系数矩阵的QR分解后，则可利用对称共轭梯度法对式(23)进行求解。获得满意解g*RQ后，利用g*=QTg*RQ获得需要的灰度值向量。其中系数矩阵的QR分解可离线计算。

使用对称共轭梯度法对方程组求解时，设方程迭代解的初始值g(0)RQ，经过k步迭代后的解为g(k)RQ。设系数矩阵SRQ的最大特征值为β，最小特征值为α。根据共轭梯度法的求解原理和数学归纳法可以得出方程经过k步迭代后解的收敛性公式如下［16］

根据QR分解的原理可以得出SRQ≈I，所以β≈α，因此经过单步计算方程解得收敛性公式为

由上式可知，方程在经过单步计算后必收敛，从而理论上证明了基于QR分解的对称共轭梯度法的单步成像的合理性。

4 实验仿真与结果分析

为判定算法的有效性，设计停止迭代误差为

设定停止迭代误差限值为1×10－6，则共轭梯度法、对称共轭梯度法和基于QR分解的对称共轭梯度法的成像误差和迭代次数以及达到停止迭代误差的时间如表1、表2、表3所示。

表1 三种算法的迭代步数

表2 三种算法的迭代误差

表3 三种算法的迭代时间 单位:ms

由表1、2、3可见，对称共轭梯度算法与共轭梯度算法相比，明显减少了迭代次数，具有更快的收敛速度。而基于QR分解的对称共轭梯度法，仅需要一步迭代，其迭代误差的数量级便可达到10－15，远优于本文所设定的停止迭代误差限值。

仿真实验中，在Intel Core 2 CPU，2GB内存的PC机上，利用COMSOL软件和Matlab软件，采用16电极仿真模型，管道内径为200.5 mm，管壁厚度6.5 mm。三种流型的管内剖分单元数分别为2 148、3 460、1 584。油井内的动态情况通常是油、气、水混合流体在钢质套管内流动，井内流体来自于地层孔间缝隙，地层油和天然气的电导率一般为10－9S·m－1～10－16S·m－1，而地层水由于绝大部分含有一定浓度的盐离子，其电导率一般为 50 S·m－1～0.5 S·m－1。仿真实验中介质电导率设为35.869 S·m－1。仿真原图如表4所示，仿真结果如表5所示，其中共轭梯度法和对称共轭梯度法各迭代500次，基于QR分解的对称共轭梯度法迭代1次完成。

表4 仿真原型

表5 三种算法的仿真结果

5 结论

本文提出的SCG算法明显提高了成像实时性，改善了重建图像质量。在此基础上提出RQSCG，实现了一步迭代成像。并对多相流ERT系统进行图像重建，其成像质量和重建速度与共轭梯度法算法进行比较。仿真实验结果表明，SCG算法、RQSCG算法对重建图像质量有明显的改进，而RQSCG算法的实时性明显优于CG和SCG算法。

［1］马艺馨，徐苓安，姜常珍.电阻层析成像技术的研究［J］.仪器仪表学报，2001，22(2):195－198，213.

［2］BrownB H.MedicalImpedance Tomography and Process Impedance Tomography:a Brief Review［J］.Meas.Sci.Technol.，2001，12:991－996.

［3］Brown B H，Barber D C.Electrical Impedance Tomography:the Construction and Application of Electrical Impedance Images［J］.Medical Progress through Technology，1987，13:69－75.

［4］张雪辉，王化祥.电容层析成像数字化系统设计［J］.传感技术学报，2007，20(8):1826－1830.

［5］孙青，王化祥.一种新型网丝传感器优化设计［J］.传感技术学报，2010，23(4):465－470.

［6］Yang Wuqiang，Peng Lihui.Image Reconstruction Algorithms for Electrical Capacitance Tomography［J］.Measurement Science and Technology，2003，14:1－13.

［7］唐磊.电学成像系统图像重建算法研究及可视化软件设计［D］.天津:天津大学，2008

［8］Vauhkonen M，Vadasz D，Kaipio J P，et al.Electrical Impedance Tomography with Basis Constraints［M］.Inverse Problems，1997，13:523－530.

［9］Hanke M.Conjugate Gradient Type Methods for Ill Posed Problems［M］.Scientific ＆ Technical，Longman，Harlow，1995.

［10］Rajen Manicon Murugan.An Improved Electrical Impedance Tomography(EIT)Algorithm for the Detection and Diagnosis of Early Stages ofBreastCancer［D］.PHD thesis，University of Manitoba，1999.

［11］邓乃扬.无约束最优化计算方法［M］.北京:科学出版社，1982.

［12］WH Winston.Tikhonov A N and Arsenin V Y，Solutions of illposed problems［M］.V.H.Winston ＆ Sons，a Division of Scripta Technica，Inc，1977.

［13］刘东毅，邵琛.下降对称的 Polak-Ribiere-Polyak共轭梯度法［J］.天津大学学报，2010，43(4):367－372.

［14］戴华.矩阵论［M］.北京:科学出版社，2001

［15］和斌涛.初等变换与矩阵的QR分解的关系［J］.科学技术与工程，2009，9(21):6484－6485.

［16］李爱芹.线性方程组的迭代解法［J］.科学技术与工程，2007，7(14):3357－3364.