基于自适应加权与LZW的WSNs层次式数据融合算法*

张志伟，王新才，吉爱国，谢 磊

(1.青岛理工大学理学院，山东青岛2660332.青岛理工大学 通信学院，山东 青岛266033)

无线传感器网络(Wireless Sensor Networks，WSNs)中，传感器节点具有的能量、处理能力、存储能力和通信能力等都十分有限，需要整个网络具有较高覆盖密度来保证鲁棒性和信息的准确收集［1］。相邻节点间收集的数据存在一定的冗余，浪费了通信带宽和整个网络的能量，降低了信息收集的效率。为了降低整个网络的能耗，提高数据收集的准确性和效率，传感器节点需要在网络内部协同地处理所收集的数据。数据融合技术(Data Aggregation)很好的解决了上述问题［2－3］。

自适应加权算法具有实现简单、精度高的特点，被用于各种数据采集仪器、仪表和监测系统中，在无线传感器网络的数据融合应用中所见不多。LZW是一种无损的，基于词典的压缩算法，由Lemple-Ziv-Welch三人共同创造。数据压缩(Data Compression)是另一类减少传感器节点采集数据传输量的技术［4］。LZW压缩算法在PC中得到广泛的应用，但是在无线传感器网络中应用很少。根据无线传感器网络数据多跳逐层上传的特点［5］，本文在前人工作基础上提出了一种层次式数据融合算法，从不同的角度对数据进行融合处理。

1 基本理论

1.1 自适应加权算法

从含有噪声的大量测量数据中估计一个非随机量，由于测量的数据中存在噪声，那么依据这些测量数据得到的估计值也存在估计误差，该估计误差也是一个随机量，我们用均方误差作为评价一个估计算法好坏的指标。自适应加权估计算法只需依靠各传感器节点提供的采集数据，就可以自适应的寻找其对应的权数估计出均方误差最小的值。

根据自适应加权算法［6］，设n个传感器采集数据的方差分别为所需估计的真值为X，各传感器采集数据的测量值分别为 X1，X2，…，Xn。它们彼此相互独立，并且是X的无偏估计;各传感器采集数据的加权因子分别为W1，W2，…，Wn则估计后的值和加权因子满足以下两式:

总均方差为:

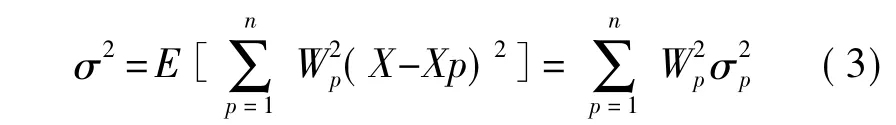
根据多元函数求极值的相关理论，可以求出总均方误差最小时所对应的加权因子为:

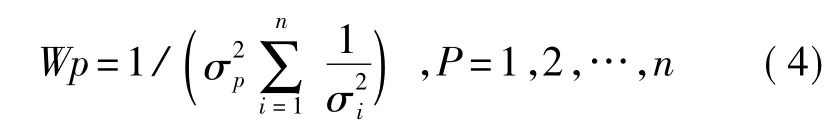
此时所对应的最小均方误差为:

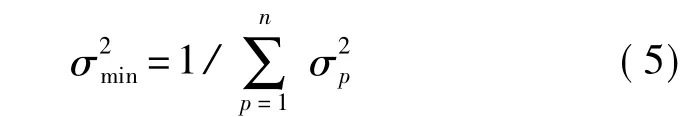
1.2 LZW算法

LZW压缩算法［7－10］是基于字典的无损压缩方法，在编码过程中动态生成编码字典，该字典不需要通信线路传给解码器，在解码过程中，动态生成编码过程完全一致的解码字典。

1.3 层次式数据融合算法

n个传感器节点采集的数据值分别为X1，X2，…，Xn，数据值对应的方差分别为簇头节点接受n个传感器节点采集的数据值和对应的方差后，根据式(4)计算出各传感器节点对应的权值并为各个传感器节点分配相应的权值;簇头节点根据式(1)计算出估计值并存储。

当簇头节点存储的估计值到一定的信息量时，簇头节点调用LZW压缩算法，对输入的数据流进行分析，在对存储的数据进行编码的同时自适应地生成一个串表，此串表记录了所有在此前出现过的不重复的字符串。通过将当前的输入数据流与该串表中字符串的比较来确定输出值并完成对串表的更新。簇头节点将数据压缩后再在网内传输，减少了网内传输的数据量。

层次式数据融合算法在提高数据采集精度的前提下，减少了网络数据传输的路径，簇头节点将数据压缩后再传输减少了网络数据传输的数据量，从而降低了网络的整体能耗。

2 层次式数据融合算法建模

2.1 WSNs簇状网络拓扑结构

当前无线传感器网络的数据融合方案可以分为:集中式融合［3］、基于树的融合［11］、静态分簇融合［12］和动态分簇融合［13］。从网内数据融合处理、数据采集的精度、网络数据采集的效率综合考虑，本文采用静态分簇的融合方案。无线传感器簇状网络拓扑结构［14］如图1所示。

图1 无线传感器簇状网络拓扑结构

2.2 LZW算法性能测试

目前，针对无线传感器网络的无损数据压缩研究还处于探索和起步阶段，压缩率是衡量算法好坏的根本标志，但是在无线传感器网络中，能量要作为衡量算法的最重要因素。考虑到数据压缩对压缩节点本身能耗及网络路由节点所产生的影响，本文对现有的成熟的压缩算法 LZW、LZO、LZSS、Zlib在IAR EW8051集成开发环境下进行测试，设定IAR的芯片开发目标是CC2430并对其他参数做配置，将各算法在IAR中进行调试，找到Debug目录下的List目录，List目录下的*.map文件详细的描述了算法运行时占用的ROM、RAM及其他参数。各算法基于 CC2430［15－16］平台测试结果如图 2、图 3 所示，图2为各个数据压缩算法运行时所需要的RAM，图3为不同的算法压缩528 B的数据计算的次数。从图2和图3可以直观的看出，从算法运行时占用的RAM和压缩相同数据量时计算的次数综合考虑，LZW压缩算法适合资源受限的传感器节点使用。根据实验测试，当系统的词典为512 B，一个压缩的数据包为410 B时，压缩算法的压缩率可以到达1.28，具有较好的压缩性能。512个条目的词典大约占用2 618 B的RAM和1 262 B的Flash Memory，适合无线传感器网络中数据融合的应用。

图2 不同算法使用RAM值

图3 不同算法等价的计算次数

2.3 自适应加权与LZW层次式数据融合应用模型

根据自适应加权与LZW层次式数据融合算法的原理，为了消除疏失误差的影响，提高测量精度，无线传感器节点每1 s进行一次采样，采集8个数据作算术平均并计算出方差后发送给簇头节点，簇头节点对接收到的多个无线传感器节点数据去除最大值与最小值，然后根据自适应算法进行数据估计，再以410 B打包压缩后以多跳通信的方式发送给汇聚节点，其应用模型如图4所示。

图4 自适应加权与LZW层次式数据融合应用模型

3 算法仿真分析

3.1 测试过程

本算法用MATLAB以图1簇状网络拓扑结构中的簇头节点A为仿真对象，测试簇头节点A采用自适应加权与LZW层次式数据融合算法时以簇头A为中心所组成的网络的整体能耗。

编程实现簇头节点A内八个传感器节点(a1、a2、a3、a4、a5、a6、a7、a8)间隔1 s采集数据八次，在传感器节点内分别对采集的数据计算平均值、方差;传感器节点将均值和方差传递给A，A收到八个点的数据后去掉最大值与最小值，然后依据自适应加权算法对数据进行融合处理;A簇内的节点不断的给簇头A发送数据，簇头A接收到数据进行融合处理后，以410 B为单位进行打包压缩，然后以多跳通信的方式，将采集的信息传递到汇聚节点。

3.2 实验仿真与分析

仿真测试结果如图5所示。

图5 算法仿真效果图

图5中，◇表示不采用融合算法时整个网络的能耗，网络的总体能耗约为2.4×106nJ;☆表示采用自适应加权算法时整个网络的能耗，网络的总体能耗约为1.1×106nJ;*表示采用自适应加权与LZW层次式数据融合算法时整个网络的能耗，网络的总体能耗约为0.9×106nJ。由仿真结果知，采用自适应加权算法，整个网络的能耗降低了约54%;采用自适应加权与LZW层次式数据融合算法，整个网络的能耗降低了约62%。因此，本文提出的算法能有效的降低无线传感器网络整个网络的能耗。

簇头节点一次采集的数据如表1所示，对表1数据分别进行层次式数据融合算法和算术平均处理。

表1 传感器簇头节点一次采集的数据

计算融合值:^X1=25.1143，此时方差为0.165 5;8个传感节点采集数据的算术平均值为25.080 0，方差为0.298 5。将数据融合算法处理后的值、方差分别与各个传感器节点采集的数据、方差及算术平均后的值、方差进行对比。

从以上数据分析知，多个无线传感器节点采用自适应加权与LZW层次式融合算法得出的估计值比单个传感器节点和多个传感器节点采集的数据算术平均估计的方差都要小，本算法提高了无线传感器网络数据采集的精度。

4 结论

本文提出了基于自适应加权与LZW的层次数据融合算法:终端数据采集节点将采集的数据算术平均后传递给簇头节点;簇头节点将各个传感器节点送来的数据以自适应加权进行融合处理，再将融合后的数据以410 B进行打包，用LZW压缩算法压缩后以多跳通信的方式传递到网关节点。

仿真结果表明，应用基于自适应加权与LZW的层次式数据融合算法可以有效地降低整个网络的能耗、提高数据采集的精度及网络数据采集的效率，有一定的实用价值。

［1］孙利民，李建中，陈渝，等.无线传感器网络［M］.北京:清华大学出版社，2005:3－4，74.

［2］Heidemann J.Building Efficient Wireless Sensor Networks with Low-Level Naming［C］//18th ACM Symposium on Operating Systems Principles，October 2001:21－24.

［3］张强，卢潇，崔晓臣.基于分簇的无线传感器网络数据聚合方案研究［J］.传感技术学报，2010，(12):1778－1779.

［4］于宏毅，李鸥，张效义.无线传感器网络理论、技术与实现［M］.国防工业出版社，2008:203－207.

［5］Zhang Zhiwei，Wang Xincai，Ji Aiguo，et al.Design of Embedded Gateway of Wireless Sensor Networks Based on Dual-MCU［C］//ICIIE 2011:V1－57.

［6］周益明.基于无线传感器网络的温室群监测与控制系统的关键技术研究与实现［D］.杭州:浙江大学，2009:69－72.

［7］Mark Nelson.The Data Compression Book［M］.America:IDG Books Worldwide，Inc:181－194.

［8］Terry Welch.A Technique for High-Performance Data Compression［J］.IEEE Computer，1984，9(17): － .

［9］Ziv J，Lempel A.A Universal Algorithm for Sequential Data Compression［J］.IEEE Transactions on Information Theory，May 1977:337－343.

［10］DuncanBarclay.LZW_compression［EB/OL］.http://www.mathworks.com/matlabcentral/fileexchange/15428，2007.

［11］Bhaskar Krishnamachari，Deborah Estrin，Stephen B Wicker.The Impact of Data Aggregation in Wireless Sensor networks［C］//ICDCSW’02:Proceedings of the 22nd International Conference on Distributed Computing Systems，2002，575－578.

［12］Ghiasi S，Srivastava A，Yang X J，et al.Optimal Energy Aware Clustering in sensor Networks［J］.Special Issue:Special Section on Sensor Network Technology and Sensor Data Management，July 2004，2:258－269.

［13］WeiPeng Chen，Jennifer C Hou，Lui Sha.Dynamic Clustering for Acoustic Target Tracking in Wireless Sensor Networks［J］.IEEE Transactions on Mobile Computing，July－Aug 2004，3:258－271.

［14］张品，姜亚光，陈磊.基于加权优化选择两级簇头的WSN路由协议［J］.传感技术学报，2011，(3):448－449.

［15］Texas Instruments.System on Chip Solution for 2.4GHzIEEE802.15.4/ZigBee［S］.2007.

［16］Texas Instruments.Texas Instruments ZStack－1.4.3－1.2.1 Documents［S］.2008.